Яким вимогам повинен відповідати ОП інвертора імпедансу?
Які коефіцієнти підсилення каскадів к1 та к2 помножувача ємності?
Які опори (вхідний, вихідний) повинні бути забезпечені в помножувачі ємності?
5 Активні фільтри
5.1 Загальні відомості про фільтри
При використанні ОП як одного з елементів пристрою з'являється можливість синтезувати характеристику будь–якого LC фільтра без використання котушок індуктивності. Такі фільтри відомі під назвою «активних фільтрів», у зв’язку з наявністю в схемі активного елемента (ОП).
Активні фільтри можна використовувати для реалізації фільтрів НЧ,ВЧ, смугопроникальних і смугозатримувальних, вибираючи тип фільтра у залежності від його властивостей; рівномірності підсилення в смузі пропускання, крутості перехідної ділянки АЧХ або незалежності часу затримки від частоти. Окрім цього можна також побудувати «усепроникаючі фільтри» з плоскою АЧХ, але нестандартною ФЧХ (такі фільтри називають «фазові коректори»), або навпаки фільтри з постійним фазовим зсувом, але довільною АЧХ.
Коефіцієнт передачі фільтра у загальному випадку можна записати у вигляді
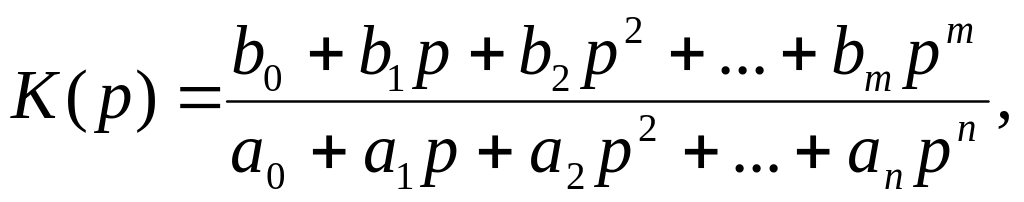(5.1)
де
–
дійсні числа; р
– оператор Лапласа, для синусоїдального
сигналу
.
Порядок
фільтра визначається найбільшим степенем
оператора р
у знаменнику. Якщо відомі корені
чисельника і корені
знаменника, то коефіцієнт передачі
можна записати у вигляді
(5.2)
При
коефіцієнт передачі дорівнює нулю, тому
корені
називають нулями. При
коефіцієнт передачі дорівнює
нескінченності, тому корені
називають полюсами.
Коефіцієнт
передачі фільтра повністю визначається
значеннями нулів і полюсів, а також
сталим множником
Коефіцієнт передачі фільтра першого порядку
(5.3)
де
У
відповідності з виразом (5.3) коефіцієнт
передачі фільтра НЧ може бути записаний
при
для
ФВЧ, при
для
фазового коректора, при
,
Коефіцієнт передачі фільтра другого порядку
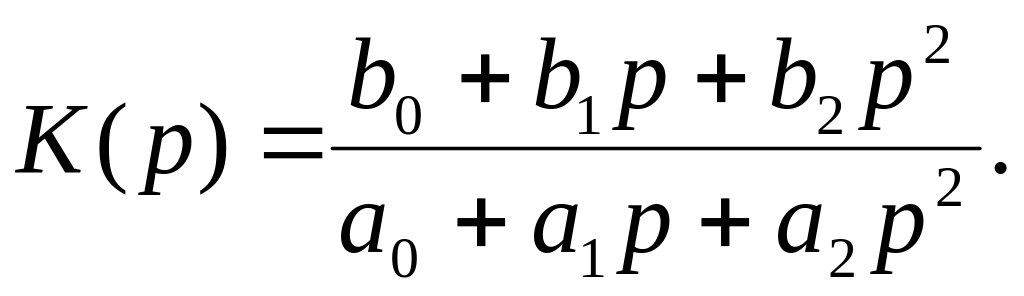(5.4)
Виходячи з виразу (5.4), коефіцієнт передачі відповідних фільтрів можна подати у вигляді:
для
ФНЧ, при
для
ФВЧ, при
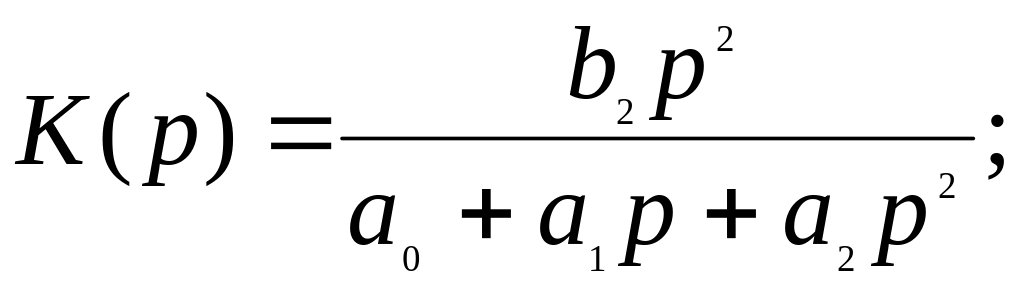
для
смугопроникального фільтра, при
для
смугозатримувальних фільтрів, при
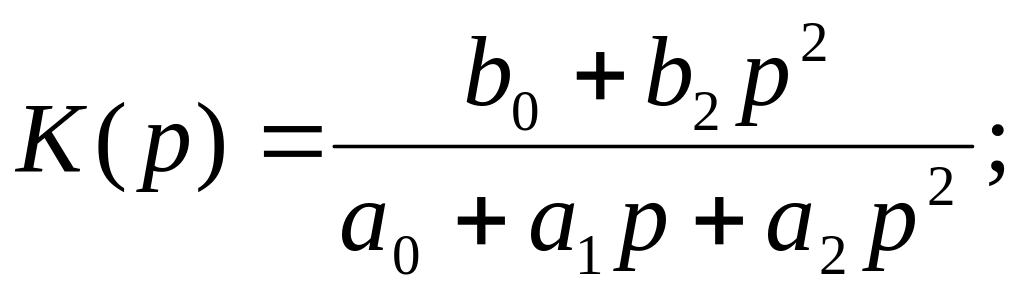
для
фазового коректора, при
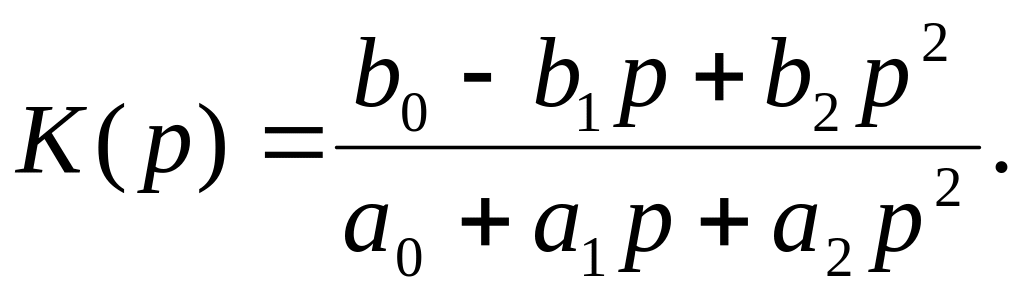
Фільтри другого порядку можна реалізувати, з'єднуючи відповідним чином ланки першого і нульового порядку. Спосіб такої реалізації витікає з можливої форми подання коефіцієнта передачі у вигляді елементарних функцій інтегрування, диференціювання, підсумовування. Оскільки способів подання виразу (5.4) через елементарні функції може бути досить багато, то і число можливих схемних рішень фільтрів другого порядку може бути значним.
На
практиці фільтр характеризується трьома
основними параметрами:
–
характеристична частота (зрізу), що
характеризує рівень послаблення АЧХ
–3 дБ;
модуль коефіцієнта передачі у смузі
пропускання;
–
коефіцієнт згасання коливань.
Смуга пропускання і добротність Q пов'язані з коефіцієнтом згасання співвідношенням
Відомі три найбільш популярні типи активних фільтрів: Баттерворта, (максимально плоска характеристика в смузі пропускання), фільтр Чебишева (найбільш крутий перехід від смуги пропускання до смуги придушення) та фільтр Бесселя (максимально плоска характеристика часу затримки). Будь–який з цих фільтрів можна реалізувати за допомогою різних схем. Всі вони придатні для побудови фільтрів верхніх, нижніх частот і смугових фільтрів.
5.2 Фільтри Баттерворта і Чебишева
Фільтр Баттерворта, як відзначено вище, забезпечує найбільш плоску характеристику в смузі пропускання, що однак досягається за рахунок повільної зміни характеристики у перехідній області, тобто між смугами пропускання і затримки. Він також має погану фазочастотну характеристику, тобто таку, що викликає значні фазові спотворення. Його амплітудно–частотна характеристика задається таким виразом
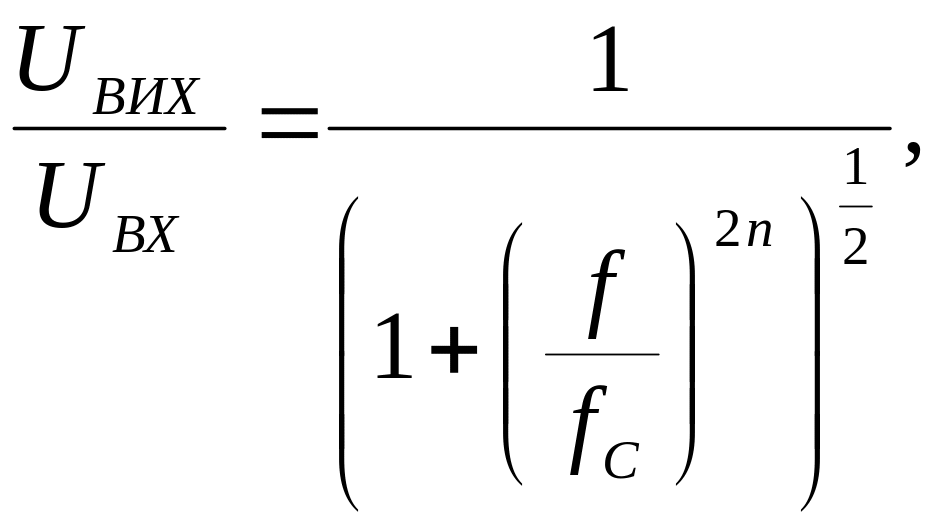(5.5)
де
n
– визначає порядок фільтра (число
полюсів);
–
частота зрізу.