Нахождение координат вектора в данном базисе

ЗАДАЧА № 8

В параллелепипеде АВСДА₁В₁С₁Д₁ К – середина ребра АА₁, точка М лежит на ребре ВС и ВМ = 2/3 ВС, О = А₁С₁ В₁Д₁. Найти координаты вектора ДО в базисе (ВК, ВА, ВМ) .

РЕШЕНИЕ

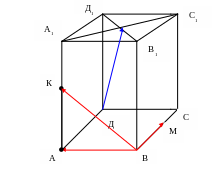
Так как координаты вектора в данном базисе это коэффициенты разложения этого вектора по векторам базиса, то данную задачу можно сформулировать так: выразить вектор ДО через векторы ВК, ВА, ВМ, поэтому будем действовать так же, как при решении задачи № 3.

1) ДО = ДД₁ + Д₁О = АА₁ + ½ Д₁В₁ = 2 АК + ½ ДВ. Т.е.

ДО = 2 АК + ½ ДВ. (1).

2) Выразим вектор АК через базисные векторы.

АК = АВ + ВК = -ВА + ВК (2)

3) Выразим вектор ДВ через базисные векторы.

ДВ = ДА + АВ = СВ + АВ = -3/2 ВМ – ВА (3)

4) Подставим (2) и (3) в (1), получим

ДО = 2(-ВА + ВК ) + ½ (-3/2 ВМ – ВА ) = 2 ВК – 5/2 ВА – 3/4 ВМ

Следовательно, первая координата вектора ДО равна 2, вторая координата равна -5/2. третья координата равна -3/4, т.е. ДО(2, -5/2, -3/4 ).

ОТВЕТ. ДО (2, -5/2, -3/4)

33. АВСД – тетраэдр. М и К – точки пересечения медиан граней ВСД и АДС, N – середина АВ, Р ВС и ВР : РС = 1 : 2. Найти координаты векторов АМ, NР, КР, NМ в базисе (АВ, АС, АД) .

34. АВСД – тетраэдр. N и К середины ребер ВС и АС. Найти координаты векторов АД и СА в базисе (ДВ, Д N, ДК) .

35. В тетраэдре АВСД М- середина ВС, а N – точка пересечения медиан грани АДС. Найти координаты векторов ДС и ВN в базисе (АВ, АД, АМ).

36. В тетраэдре АВСД N - середина ВС, а М – точка пересечения медиан грани ВСД. Найти координаты векторов С N и МК в базисе ( АМ, АВ, АД).

37.АВСДА₁В₁С₁Д₁ – параллелепипед. А₁С₁ В1Д1 = М, К – середина ДД1, Р ВС и ВР = 2/3 ВС. Найти координаты векторов ВК, МС, А₁Р в базисе (АВ, АД, АД₁)

38. АВСД А₁В₁С₁Д₁ – параллелепипед. АС ВД = М . Найти координаты векторов В1С и АС1, в базисе (Д₁М, Д₁Д, Д₁А).

39. АВСД А₁В₁С₁Д₁ – параллелепипед. А₁С₁ В1Д₁ = М.Найти координаты векторов ДС, Д₁В, С₁А в базисе (МА, МВ, МС) .

40. SАВСД – правильная четырехугольная пирамида с основание АВС Д. К SА и SК = 1/3 SА , N – середина SС, АС ВД = М. Найти координаты векторов СР и А N в базисе (SК, SД, SМ).

41. SАВСД – правильная четырехугольная пирамида с основание АВС Д. АС ВД = М, О – середина SМ, N – точка пересечения медиан грани ВСS. Найти координаты вектора Д N в базисе (АS, АО, АВ)

Скалярное произведение векторов

Скалярным произведением векторов а и b называется число, равное произведения длин этих векторов и косинуса угла между ними

а b = │а││b│cos (аb).

Скалярное произведение векторов обладает следующими свойствами. Для любых векторов а, b, c и любого числа λ

1) а b = b a, 2) (a + b) c = a c + b c, 3) (λ a) b = a (λ b) = λ (a b).

Если известны координаты векторов а и b в ортонормированном базисе {i, j, k } а(а₁,а₂,а₃), b(b₁,b₂,b₃), то имеют место формулы

___________

a b = а₁ b₁ + а₂ b₂ + а₃ b₃, │а│= √а₁² + а₂² + а₃²

______а₁ b₁ + а₂ b₂ + а₃ b₃____

cos (а, b) = √а₁² + а₂² + а₃² √b₁² + b₂² + b₃²

42. АВСД – ромб с углом А равным 60° и стороной АВ равной 4. Найти скалярное произведение ДА ДВ.

43. М – точка пересечения медиан равностороннего треугольника АВС со стороной равной 2. Найти скалярное произведение МА МВ.

44. АВСД – квадрат стороной равной 5. Найти скалярное произведение АВ СА.

ЗАДАЧА № 9

Даны неколлинеарные векторы а и в. Дать геометрическое истолкование формулы (а + в)² + (а – в)² = 2(а² + в² )

РЕШЕНИЕ

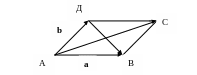
От произвольной точки А отложим векторы АВ = а, АД = в и построим параллелограмм АВСД. Тогда АВ = ДС = а, АД = ВС = в , АС = а + в, ДВ = а – в. Так как скалярный квадрат вектора равен квадрату его длины, то (а + в)² = |а + в|² = | АС |² =| АС |², (а – в)² = |а - в|² = | ДВ |² = | ДВ |² ,

а² =|а |² = | АВ |² = | АС |² = | АВ |² = | АС |², в² =|в|² = | АД |² = | ВС |² =

| АД |² = | ВС |².

Следовательно, данное равенство (а + в)² + (а – в)² = 2(а² + в² )

можно переписать в виде | АС |² + | ДВ |² = | АВ |² + | АС |² +

+ | АД |² + | ВС |² .Таким образом, данное в условии равенство имеет следующее геометрическое истолкование:

В параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон. ■

45. Даны неколлинеарные векторы а и в . Дать геометрическое истолкование формул 1) (а + в)² - (а – в)² = 4а в, 2) (а + в) (а – в) = а² - в² .

46. Какие из следующих равенств являются верными для любых входящих в них векторов 1) |а | а = а², 2) (а + в)² = а² + 2ав + в² , 3) (а в)² = а² в² ?

ЗАДАЧА № 10

Дан базис {е₁,е₂,е₃}. Зная координаты векторов а(а₁,а₂,а₃), в(в₁,в₂,в₃), длины базисных векторов и углы между базисными векторами, выразить скалярное произведение векторов а и в через их координаты в данном базисе.

РЕШЕНИЕ

Так как а(а₁,а₂,а₃), в(в₁,в₂,в₃), то по определению координат вектора, получим: а = а₁ е₁ + а₂ е₂ + а₃ е₃, в = в₁ е₁ + в₂ е₂ + в₃ е₃. Тогда, подставив в скалярное произведение а в вместо векторов а и в их разложение по базисным вектора и используя свойства скалярного произведения, получим

а в = (а₁ е₁ + а₂ е₂ + а₃ е₃)(в₁ е₁ + в₂ е₂ + в₃ е₃) = а₁ в₁ (е₁е₁) + а₂ в₂ (е₂е₂) +

а₃в₃( е₃е₃) + (а₁в₂ + а₂в₁)(е₁е₂) + (а₁в₃ + а₃ в₁)(е₁е₃) + (а₂в₃ + а₃в₂)(е₂е₃) = а₁в₁│е₁│² + а₂в₂│е₂│² + а₃в₃│е₃│² + (а₁в₂ + а₂в₁)│е₁││е₂│Соs (е₁,е₂) + (а₁в₃ + а₃в₁)│е₁││е₃│Соs (е₁,е₃) +(а₂в₃ + а₃в₂)│е₂││е₃│Соs (е₂,е₃).

ОТВЕТ.

а в = а₁в₁│е₁│² + а₂в₂│е₂│² + а₃в₃│е₃│² + (а₁в₂ + а₂в₁)│е₁││е₂│Соs (е₁,е₂) + (а₁в₃ + а₃в₁)│е₁││е₃│Соs (е₁,е₃) +(а₂в₃ + а₃в₂)│е₂││е₃│Соs (е₂,е₃).

Таким образом, чтобы найти скалярное произведение векторов, зная их координаты в произвольном базисе, надо знать еще длины базисных векторов и углы между ними.

ЗАМЕЧАНИЕ Во всех задачах этого пункта будем считать, что дан ортонормированный базис

47. а(1,-1,3), в(2,4,-5), с(1,-2,1). Найти: 1) а в, 2) | с |, 3) Соs ( в, с).

4) (а + в + 5с) · (2в -4с), 5) (а – в) · (с – а) .

48.В параллелограмме АВСД АВ(-8,0,6), ДА(-3,-4,0). Найти ВАД.

49. Найти косинусы углов, образованных вектором а(5, - , 3)

с базисными векторами i, j, k.

50. Дан тетраэдр АВСД. АВ(1,4,1), АС(2,-3,-2), АД(0,5,0). Найти Соs ВАМ, где М – середина СД.

51. МАВСД – четырехугольная пирамида, основание которой – параллелограмм АВСД. К и Р – середины сторон АВ и ВС. ВА(6,0,-4), ВС(4,4,10), ВМ(1,-2,3). Найти 1) | АС |, 2) Соs КМР.

52. В пространственном четырехугольнике АВСД АВ(1,6,-2), ВС(5,3,-1), СД(1,-7,1). Доказать, что диагонали четырехугольника перпендикуляры.

53. Дан четырехугольник АВСД. АВ(6,0,-8), ВС(0,10,0), СД(-6,0,8). Доказать, что этот четырехугольник является квадратом.

54. Найти длину медианы АМ треугольника АВС и угол АМВ, если АВ(1,-1,2), АС(3,5,-4).

55. Объяснить, почему для любых векторов а, в, с не выполняется равенство (а в) с = а ( в с) ? Найти все векторы а, в, с для которых это равенство выполняется.

ЗАДАЧА № 11

АД – биссектриса треугольника АВС. Выразить вектор АД через векторы АВ и АС.

РЕШЕНИЕ.

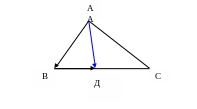
1. АД = АВ + ВД = АВ + х ВС = АВ + х (АС – АВ) или

АД = АВ + х (АС - АВ ) (1)

2. Найдем коэффициент х, для которого ВД = х ВС. Так как векторы

ВД и ВС сонаправлены, то коэффициент х положителен. Из определения произведения вектора на число получим, что |ВД | =│х│ | ВС | = х | ВС |, а отсюда следует, что

х = (2)

3) Так как АД – биссектриса треугольника АВС, то по свойству биссектрисы треугольника получаем, что

= (3)

= = - 1 или

= + 1 (4)

Из (3) и (4) следует, что = + 1 = , отсюда и из (2) получаем, что х = . Поставляем это значение х в (1) и получаем

АД = АВ + . (АС - АВ ) = ( 1 - ) АВ + АС или

АД = АВ + АС (5)

ОТВЕТ. Если АД - биссектриса треугольника АВС, то

АД = АВ + АС.

ЗАДАЧА № 12

АН – высота треугольника АВС. Выразить вектор АН через векторы АВ и АС.

РЕШЕНИЕ.

В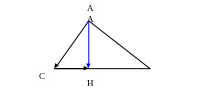

1) АН = АВ + ВН = АВ + х ВС = АВ + х (АС – АВ) или

АН = АВ + х (АС - АВ ) (1)

2) Найдем коэффициент х, для которого ВН = х ВС.

Так как АН – высота треугольника АВС, то АН ВС, значит АН ВС, поэтому скалярное произведение АН ВС = 0. Подставим в это соотношение вместо АН его выражение из (1), получим

[АВ + х (АС - АВ ) ] ВС = 0 , по свойству скалярного произведения можно раскрыть квадратные скобки АВ ВС + х (АС - АВ ) ВС = 0, отсюда

АВ ВС АВ(АС-АВ)

х = ------------------- или х = - ----------------- (2)

(АС – АВ) ВС (АС _ АВ)²

Подставим это значение х в формулу (1), получим

АВ(АС-АВ)

АН = АВ - ---------------- (АС – АВ) (3)

(АС – АВ)²

ОТВЕТ. Если АН – высота треугольника АВС, ТО

АВ(АС –АВ)

АН = АВ - ----------------- (АС – АВ)

(АС – АВ)²

ЗАМЕЧАНИЕ.

1) Если вам хочется упростить формулу (2), то этого делать нельзя, т.к если числитель и знаменатель дроби есть скалярные произведения а в и в в, то это числа, равные произведению длин векторов на косинус угла между ними, кроме того в векторной алгебре нет действия деления вектор на вектор.

2) Если вам хочется упростить формулу (3), то этого делать нельзя, т.к

второе слагаемое можно переписать так:

[ АВ(АС –АВ) ] (АС - АВ )

------------------------------------- ,

(АС –АВ)²

но для скалярного произведения [а в] с а [в с]., поэтому квадратные скобки во втором слагаемом формулы (3) переставить нельзя.

ЗАДАЧА № 13

Дан ортонормированный базис. В треугольнике АВС АВ(3,0,4), АС(8,0,-6) Найти а ) длину высоты АН, б) угол между медианой АМ и биссектрисой АД.

РЕШЕНИЕ

1) Найдем координаты вектора АН и его длину. По задаче № 10

АВ(АС-АВ)

АН = АВ - ------------------ (АС – АВ). Сначала найдем, чему равно число х=

(АС – АВ)²

АВ(АС-АВ)

(АС – АВ)² . Так как АВ(3,0, 4) АС(8, 0,-6), то (АС – АВ)(5,0,-10), то

х = = = .

Тогда АН = АВ + 1/5 (АС – АВ), отсюда найдем координаты вектора АН.

АН(4, 0, 2), тогда │АН│= = 2

АМ АД

2) Воспользуемся формулой Соs МАД = |АМ| |АД|

3) Найдем координаты вектора АМ и его длину. Так как АМ = ½ (АВ + АВ), то АМ(5/2, 3, 2) и |АМ | = = /2.

4)Найдем координаты вектора АД и его длину .

По задаче № 9 АД = АВ + АС.

Так как АВ(3,0,4) АС(8, 0,-6), поэтому АВ =│АВ│= = 5, АС=│АС│= =10, тогда АД = 2/3 АВ + 1/3 АС, поэтому

АД(14 / 3, 0, 2 / 3)

и │АД│= =

АМ АД 70/6 + 0 + 4/3 39

5) Соs МАД = |АМ| |АД| = 10 /6 = 720

ОТВЕТ. |АМ | = / 2, Соs МАД = 39

720

56. Найти длины медианы АД и высоты АН треугольника АВС, если АВ(0,4,0), АС(-3, 0,0).

57. В треугольнике АВС АВ(2,1,3), АС(0,1,1) Найти косинус угла между медианой АМ и высотой АН.

58. АМ и АД медиана и биссектриса треугольника АВС. Найти косинус угла МАД, если АВ(0,4,0), АС(-3, 0,0).

59. В треугольнике АВС АМ - медиана, АД –биссектриса, АН – высота. Найти длину АМ и косинус угла НАД, если АВ(2,0,0), АС(0,0,4).

ЗАМЕЧАНИЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ 59 - 64

Если дан многогранник, в котором известны длины трех некомпланарных ребер, выходящих из одной вершины, и углы между ними, то надо рассмотреть базис {а,в,с}, который порождается этими ребрам

60. В параллелепипеде АВСД А₁В₁С₁Д₁ |АВ |= 2, |АД |= |АА₁ | = 1, А₁АВ = А₁АД = 60°, ВАД = 30°. Найти длину ВД₁.

61. В прямоугольном параллелепипеде АВСД А₁В₁С₁Д₁ |АВ |= а, |АД |=в, |АА₁ | = с. Найти угол между прямыми АС₁ и В₁Д₁.

62. В тетраэдре АВСД |АВ |= |АС |= |АД | = 3, ВАД = САД = 90°,

САВ = 60°. Найти длину ВМ, где М – середина ДС.

63. В тетраэдре АВСД |ДА |= |ДВ |= |ДС | = 2, АДВ = АДС = 90°,

СДВ = 60°. Найти длину ДМ, где М – точка пересечения медиан грани АВС.

64. В тетраэдре АВСД |ДА |=1, |ДВ |= 2, |ДС | = 3, АДС = ВДС =

АДВ = 60°. Найти угол между ДМ и ВС.

65. В правильном тетраэдре АВСД, в котором |АВ| = 3, М – точка пересечения медиан грани АВС, Р – середина АД. Найти длину МР.