
- •Вероятностно-статистические методы в энергетике
- •Введение
- •Глоссарий
- •Задача №2
- •Задача №3
- •Логическая схема анализа надежности Задача №4
- •З адача №5
- •Задача №6
- •Задача №7
- •Задача №8
- •Классическая формула определения вероятности события. Задача №9
- •Задача №10
- •Задача №11
- •Геометрическая формула определения вероятности события Задача №12
- •Статистическая формула определения вероятности события. Задача №13
- •Занятие №2
- •Формула умножения вероятностей Задача №14
- •Задача №15
- •Задача №16
- •Задача №17
- •Формула сложения вероятностей. Определение вероятности хотя бы одного события. Задача №18
- •З адача №19
- •Задача №20
- •Задача №21
- •Задача №22
- •Задача №23
- •Задача №24
- •Формула полной вероятности. Задача №25
- •Задача №26
- •Задача №27
- •Формула Бейеса. Задача №28
- •Задача №29
- •Задача №30
- •Задача №31
- •Формула Бернулли. Задача №32
- •Задача №33
- •Задача №34
- •Занятие №3 Способы задания законов распределения. Задача №35
- •Задача №36
- •Занятие №4 Параметры положения случайной величины (мода, медиана, математическое ожидание). Моменты случайной величины. Дисперсия случайной величины. Задача №41
- •Задача №42
- •Задача №43
- •Задача №44
- •Задача №45
- •Задача №46
- •Задача №47
- •Задача №48
- •Задача №49
- •Занятие №5 Биномиальный закон распределения. Закон Пуассона. Закон равномерного распределения вероятностей Задача №50
- •Задача №51
- •Задача №52
- •Занятие №6 Нормальный закон распределения (Гаусса – Лапласа). Нормальная функция распределения. Правило «3 сигма» Задача №53
- •Задача №54
- •Задача №55
- •Занятие № 7 Выравнивание статистических рядов. Проверка правдоподобия гипотез о характере закона распределения Задача №56
- •Литература
- •Оглавление
Задача №6
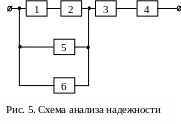 Для нижеприведенной схемы (рис. 5)
анализа надежности записать события,
заключающиеся в работоспособности
системы RС
и ее отказе
С,
обозначая состояния работоспособности
и отказа отдельных элементов как Ri
и
.
Для нижеприведенной схемы (рис. 5)
анализа надежности записать события,
заключающиеся в работоспособности
системы RС
и ее отказе
С,
обозначая состояния работоспособности
и отказа отдельных элементов как Ri
и
.
Решение.
(Решается аналогично задаче №1).
Rc=R3R4(R1R2 + R5 + R6);
с= 3+ 4+ 6 5( 1+ 2).
Задача №7
Для нижеприведенной схемы (рис. 6) анализа надежности записать события, заключающиеся в работоспособности системы и ее отказе, обозначая состояния работоспособности и отказа отдельных элементов как Ri и .
Решение. (Решается аналогично задаче №1).
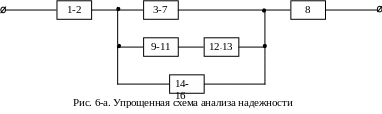
Сначала производится упрощение исходной схемы анализа надежности путем замены последовательно соединенных элементов новыми эквивалентными элементами, для которых описываются их состояния через состояния исходных элементов, (рис. 6-а): R1-2 = R1R2; 1-2 = +
R3-7
= R3R4R5R6R7;
3-7
=
+
+
+
+
![]() ;
;
R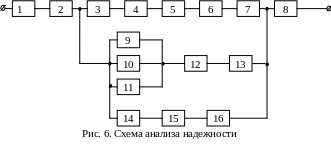 9-11
= R9
+ R1
0+ R11;
9-11
=
9-11
= R9
+ R1
0+ R11;
9-11
=
![]()
![]()
![]() ;
;
R12-13
=
R12R13;
![]() =
=
![]() +
+![]() ;
;
R14-16
= R14R15R16;
14-16
=
![]() +
+![]() +
+![]() ;
;
RС
= R1-2R8
(R3-7 +
R14-16 +
R9-11R12-13);![]()
![]()
 =
=
![]() +
+
![]() + (
+ (![]()
![]() (
(![]() +
+
![]() ))
))
Задача №8
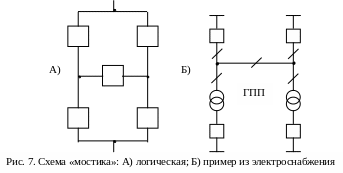 Описать состояние работоспособности
и отказа схемы «мостика» (рис.7-А). Эта
схема получила широкое распространение,
как одна из схем подстанций промышленных
предприятий и электрических сетей (Рис.
7-Б).
Описать состояние работоспособности
и отказа схемы «мостика» (рис.7-А). Эта
схема получила широкое распространение,
как одна из схем подстанций промышленных
предприятий и электрических сетей (Рис.
7-Б).
 Решение. Для описания состояния
системы целесообразно использовать
метод путей. Он заключается в том, что
намечаются все возможные пути передачи
сигнала от входа системы к её выходу.
Затем описываются состояния
работоспособности и отказа каждого из
путей. В итоге система работоспособна,
когда работоспособен хотя бы один путь.
Система отказывает, когда отказывают
все пути.
Решение. Для описания состояния
системы целесообразно использовать
метод путей. Он заключается в том, что
намечаются все возможные пути передачи
сигнала от входа системы к её выходу.
Затем описываются состояния
работоспособности и отказа каждого из
путей. В итоге система работоспособна,
когда работоспособен хотя бы один путь.
Система отказывает, когда отказывают
все пути.
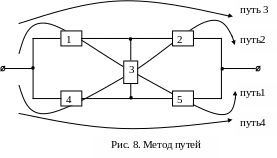
Для схемы «мостика» возможны четыре пути (рис. 8):
RП1 = R1R3R5 ; RП2 = R4R3R2 ; RП3 = R1R2 ; RП4 = R4R5
RС = R1R3R5 + R4R3R2 + R1R2 + R4R5 = R1(R3R5 + R2) + R4(R3R2 + R5);
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
Классическая формула определения вероятности события. Задача №9
При перевозке контейнера, в котором содержались 21 стандартная и 10 нестандартных деталей, была утеряна одна деталь. Определить вероятность потери:
а) стандартной детали – Р(С); б) нестандартной детали – Р(Н).
Найти те же вероятности, если одна проверенная после перевозки деталь оказалась стандартная –Р(СПР) и Р(НПР).
Решение.
В данной задаче применяется классическая формула определения вероятности события, в которой вероятность некоторого события А может быть найдена, как отношение количества исходов, благоприятствующих событию А, к общему количеству исходов опыта, удовлетворяющих схеме случаев: Р(А)=m/n,
где n – общее количество исходов опыта, удовлетворяющих схеме случаев;
m – количество исходов, благоприятствующих событию А.
Схема случаев подразумевает три обязательных условия применения классической формулы:
исходы опыта должны быть несовместными;
должны образовывать полную группу;
должны быть равновозможными.
Обозначим событие С – потерялась стандартная деталь;
событие Н – потерялась нестандартная деталь.
Так как при перевозке с равными шансами могла потеряться любая деталь, общее число исходов опыта равно 10 + 21= 31. Тогда
Р(С) = 21/31; Р(Н) = 10/31.
Когда после перевозки начата проверка деталей и выяснено, что первая проверенная деталь – стандартная, количество возможных исходов опыта сокращается. Теперь могла быть потеряна любая из десяти нестандартных деталей и любая из 20 стандартных. Поэтому
Р(СПР)
=
![]() = 20/30 = 2/3; Р(НПР) =
= 20/30 = 2/3; Р(НПР) =
![]() = 1/3.
= 1/3.
