
- •« Могилевский государственный университет продовольствия»
- •Высшая математика
- •Рассмотрены и рекомендованы к изданию на заседании кафедры высшей математики
- •Требования к выполнению и оформлению контрольных работ
- •Задания контрольной работы №1
- •Указания к решению заданий
- •Вопросы к экзамену
- •I Элементы линейной и векторной алгебры, аналитической геометрии
- •II Введение в математический анализ
- •III Дифференциальное исчисление функции одной переменной
- •IV Функции нескольких переменных
- •V Векторные и комплексные функции действительного аргумента. Функции комплексного переменного
- •Список рекомендуемой литературы
- •Высшая математика
- •212027, Могилев, пр-т Шмидта, 3.
Задания контрольной работы №1
ЗАДАНИЕ 1. Проверить, является ли система линейных уравнений
![]()
совместной и решить ее в случае совместности:
а) матричным методом. Проверить правильность нахождения обратной матрицы матричным умножением (АА – 1= А – 1А = Е);
б) методом Гаусса.
1
![]() 2
2
![]() 3
3
![]()
4
![]() 5
5
![]() 6
6
![]()
7
![]() 8
8
![]() 9
9
![]()
10
![]() 11
11
![]() 12
12
![]()
13
![]() 14
14
![]() 15
15
![]()
16
![]() 17
17
![]() 18
18
![]()
19
![]() 20
20
![]() 21
21
![]()
22
![]() 23
23
![]() 24
24
![]()
25
![]()
ЗАДАНИЕ 2. По координатам вершин пирамиды А1А2А3А4 найти:
косинус угла между ребрами А1А2 и А1А4;
площадь грани А1А2А3;
объем пирамиды;
уравнение плоскости А1А2А3;
уравнение высоты, опущенной из точки А4 на грань А1А2А3, и ее длину.
1 А1 (3; 1; 4), А2 (–1; 6; 1), А3 (–1; 1; 6), А4 (0; 4; –1).
2 А1(3; –1; 2), А2(–1; 0; 1), А3(1; 7; 3), А4(8; 5; 8).
3 А1(3; 5; 4), А2(5; 8; 3), А3(1; 2; –2), А4(–1; 0; 2).
4 А1(2; 4; 3), А2(1; 1; 5), А3(4; 9; 3), А4(3; 6; 7).
5 А1(9; 5; 5), А2(–3; 7; 1), А3(5; 7; 8), А4(6; 9; 2).
6 А1(0; 7; 1), А2(2; –1; 5), А3(1; 6; 3), А4(3; –9; 8).
7 А1(5; 5; 4), А2(1; –1; 4), А3(3; 5; 1), А4(5; 8; –1).
8 А1(6; 1; 1), А2(4; 6; 6), А3(4; 2; 0), А4(1; 2; 6).
9 А1(7; 5; 3), А2(9; 4; 4), А3(4; 5; 7), А4(7; 9; 6).
10 А1(6; 8; 2), А2(5; 4; 7), А3(2; 4; 7), А4(7; 3; 7).
11 А1(4; 2; 5), А2(0; 7; 1), А3(0; 2; 7), А4(1; 5; 0).
12 А1(4; 4; 10), А2(7; 10; 2), А3(2; 8; 4), А4(9; 6; 9).
13 А1(4; 6; 5), А2(6; 9; 4), А3(2; 10; 10), А4(7; 5; 9).
14 А1(3; 5; 4), А2(8; 7; 4), А3(5; 10; 4), А4(4; 7; 8).
15 А1(10; 9; 6), А2(2; 8; 2), А3(9; 8; 9), А4(7; 10; 3).
16 А1(1; 8; 2), А2(5; 2; 6), А3(5; 7; 4), А4(4; 10; 9).
17 А1(6; 6; 5), А2(4; 9; 5), А3(4; 6; 11), А4(6; 9; 3).
18 А1(7; 2; 2), А2(–5; 7; –7), А3(5; –3; 1), А4(2; 3; 7).
19 А1(8; –6; 4), А2(10; 5; –5), А3(5; 6; –8), А4(8; 10; 7).
20 А1(1; –1; 3), А2(6; 5; 8), А3(3; 5; 8), А4(8; 4; 1).
21 А1(1; –2; 7), А2(4; 2; 10), А3(2; 3; 5), А4(5; 3; 7).
22 А1(4; 2; 10), А2(1; 2; 0), А3(3; 5; 7), А4(2; –3; 5).
23 А1(2; 3; 5), А2(5; 3; –7), А3(1; 2; 7), А4(4; 2; 0).
24 А1(5; 3; 7), А2(–2; 3; 5), А3(4; 2; 10), А4(1; 2; 7).
25 А1(4; 3; 5), А2(1; 9; 7), А3(0; 2; 0), А4(5; 3; 10).
ЗАДАНИЕ 3. Вычислить пределы функций, не используя правило Лопиталя:
1 а)
![]() ; б)
; б)
![]() ;
;
в)
 ; г)
; г)
![]() .
.
2 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
3 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
4 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
5 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
6 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
7 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
8 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
9 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
10 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
11 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
12 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
13 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
14 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
15 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
16 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
17 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
18 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
19 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
20 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
21 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
22 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
23 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
24 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
25 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
ЗАДАНИЕ 4.
Исследовать
функцию
![]() на непрерывность: найти точки разрыва
и определить их тип. Изобразить
схематический график функции.
на непрерывность: найти точки разрыва
и определить их тип. Изобразить
схематический график функции.
1
f (x) = ![]() 2
f (x) =
2
f (x) = ![]()
3
f (x) = ![]() 4
f (x) =
4
f (x) = ![]()
5
f (x) = ![]() 6
f (x) =
6
f (x) = ![]()
7
f (x) =  8
f (x) =
8
f (x) = ![]()
9
f (x) = ![]() 10
f (x) =
10
f (x) = ![]()
11
f (x) = ![]() 12
f (x) =
12
f (x) = ![]()
13
f (x) = ![]() 14
f (x) =
14
f (x) =![]()
15
f (x) =![]() 16
f (x) =
16
f (x) = ![]()
17
f (x) = ![]() 18
f (x) =
18
f (x) = ![]()
19
f (x) = ![]() 20
f (x) =
20
f (x) =![]()
21
f (x) = ![]() 22
f (x) =
22
f (x) =![]()
23
f
(x) = ![]() 24
f (x) =
24
f (x) = ![]()
25
f (x) = ![]()
ЗАДАНИЕ 5. Найти производные первого порядка следующих функций:
1 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
2 а)
![]() + lg3; б)
+ lg3; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
3 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
4 а)
![]() ; б)
; б)
![]() ;
;
в)![]() ; г)
; г)
![]()
5 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
6 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
7 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
8 а)
![]() – tg4; б)
– tg4; б)
![]() ;
;
в)
![]() ; г)
; г)

9 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
10 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)

11 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
12 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)

13 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
14 а)
![]() ; б)
; б)
![]() ;
;
в)
exy – x2 + y2 = 0; г)

15 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)

16 а)
![]() ; б)
; б)
![]() ;
;
в)sin y = x2 – yx; г)

17 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
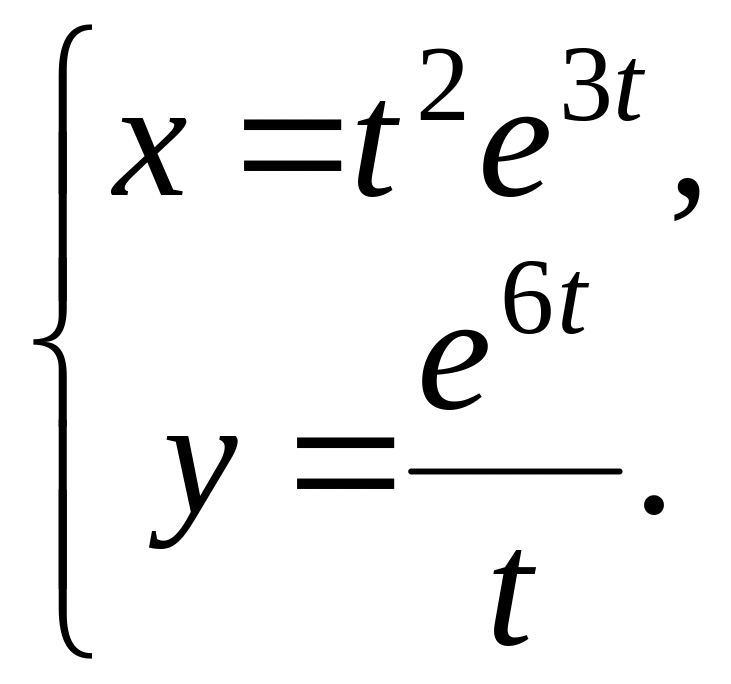
18 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
19 а)
![]() ; б)
; б)
![]()
в)
![]() ; г)
; г)
![]()
20 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)

21 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
22 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
23 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
24 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
25 а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
ЗАДАНИЕ 6.
Представить
заданную функцию комплексного переменного
![]() ,
где
,
где
![]() ,
в виде
,
в виде
![]() ;
проверить, является ли она аналитической.
Если является аналитической, найти
значение её производной в точке
;
проверить, является ли она аналитической.
Если является аналитической, найти
значение её производной в точке
![]() .
.
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10 |
|
11 |
|
12
|
. |
13
|
|
14
|
|
15
|
|
16
|
|
17
|
. |
18
|
. |
19
|
|
20
|
. |
21
|
|
22
|
|
23 , |
. |
24 |
z0 = 2 i. |
25
|
|
|
|
