5.3.3. Синтез кс в классическом базисе

Пример 5.28. ПФ, заданная СДНФ, представлена на карте Карно (рис. 5.20). Требуется реализовать КС в классическом базисе.

х₂

х1 1	1
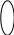
1	1	1	х3
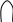
	1
1

x₄

Рис. 5.20. Минимизация функции четырех переменных

По карте Карно (рис. 5.20) найдем минимальную форму

y = f_min=x₁x₂ x₂x₃x₄ x₁x₃x₄ x_{2 .}

По структуре формулы строим схему, при этом инверсии значений аргументов получаем с помощью элементов «НЕ», конъюнкции в термах посредством элементов «И» и, наконец, объединяем термы с помощью четырех- входового элемента «ИЛИ» (рис. 5.21).

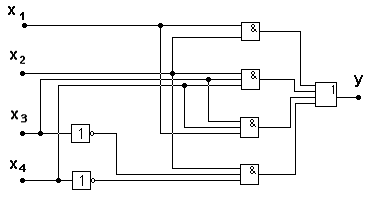
Рис. 5.21

Данная схема имеет 3 уровня, каждый из которых вносит свой вклад в задержку: 1-й уровень – инверторы, 2-й – элементы «И», 3-й – элемент «ИЛИ».

Для оценки сложности схем часто используется критерий Квайна

, (5.28)

где l_i – число элементов i-го типа,

m_i – число входов элемента i-го типа,

k – число типов логических элементов.

Таким образом, данный критерий определяется как суммарное число входов логических элементов.

Для схемы из последнего примера С = 17.

В рассмотренном примере использовалась только минимизация ПФ и производилось собственно построение схемы. Часто бывает полезно выполнить дополнительные преобразования, позволяющие снизить сложность схем. Рассмотрим следующий пример.

П

х₂

ример 5.29. Построить КС для функции, заданной на карте Карно рис. 5.22.

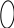
х1 1	1		1
1

x₃

Рис. 5.22. Пример функции трех переменных

По карте Карно (рис. 5.22) определяем:

y = f_min = x₁x₂  ,

в соответствии с данным выражением строим схему (рис. 5.23а). Сложность схемы по критерию Квайна соответствует С = 10.

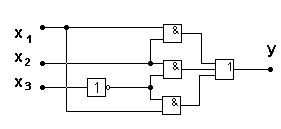
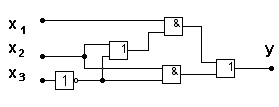
а) б)

Рис. 5.23. Пример дополнительного преобразования

Полученное выражение можно преобразовать, выполнив вынесения за скобки, например:

.

Для данного выражения КС приводится на рис. 5.23б.

Сложность данной схемы по критерию Квайна соответствует С = 9, т.е. меньше.

Очевидно, что для более сложных схем подобные преобразования могут привести к более значительным упрощениям. Однако в данном случае в схеме появляется дополнительный ранг, который будет вносить задержку в сигнал на выходе. Таким образом, упрощения схемы в данном случае производятся за счет снижения быстродействия.

В качестве дополнительных преобразований можно применить преобразования, основанные на правилах Де Моргана, которые в некоторых случаях позволяют исключить инверторы из схемы.

Пример 5.30. .

Непосредственная реализация исходного выражения требует трех логических элементов (два элемента «И» и один элемент «ИЛИ»). Преобразованное выражение может быть реализовано одним элементом «ИЛИ-НЕ».

Замечание. В некоторых случаях более эффективной (в смысле критерия Квайна) оказывается минимизация по нулям, рассмотренная в п. 5.2.6 (см. пример 5.24).