
- •1.1 Задачи математической статистики.
- •1.2 Статистическое распределение выборки.
- •2.2 Общие описательные характеристики.
- •2.3. Показатели вариации
- •§3. Законы распределения вероятностей.
- •3.1 Биноминальный закон распределения
- •3.2. Распределение Пуассона.
- •3.3 Нормальный закон распределения (нзр)
- •Показательное распределение (экспоненциальное).
- •Распределение «хи – квадрат»
- •Распределение «Стьюдента» или t-распределение
- •Распределение Фишера или f-распределение
- •§4 Проверка гипотез
§3. Законы распределения вероятностей.
3.1 Биноминальный закон распределения
Данный закон имеет место только для дискретной случайной величины. Пусть для каждого отдельного случая величина может принимать только 2 значения:
1 с вероятностью Р;
0 с вероятностью Q=1-Р.
Тогда соответствующие вероятности появления т успешных случайных величин Х вычисляется по формуле:
 (3.1)
(3.1)
3.2. Распределение Пуассона.
Если известны значения дискретной случайной величины, тогда закон распределения может быть законом Пуассона. Распределение Пуассона обычно использует в случае «редких событий», (например, определение родившихся двойняшек в городе за определенный период).
Пусть случайная величина Х, принимающая только целые положительные значения, распределена по закону распределения Пуассона с параметром λ, если:
 ,
(3.2)
,
(3.2)
где
 - интенсивность, n –
количество испытаний (наблюдений); а p
– вероятность появления события в
каждом из них.
- интенсивность, n –
количество испытаний (наблюдений); а p
– вероятность появления события в
каждом из них.
3.3 Нормальный закон распределения (нзр)
НЗР вероятности случайной величины Х имеет место только для непрерывной случайной величины и задается плотностью вероятности
 (3.3)
(3.3)
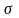 -
среднее квадратное отклонение, а –
математическое ожидание.
-
среднее квадратное отклонение, а –
математическое ожидание.
Обозначение
нормальной случайной величины:
 .
Если
.
Если
 ,
нормальная случайная величина называется
стандартной нормальной величиной.
Плотность нормализированного распределения
имеет вид
,
нормальная случайная величина называется
стандартной нормальной величиной.
Плотность нормализированного распределения
имеет вид
 .
Параметр а
определяет положение центра нормальной
плотности,
-
разброс относительно центра.
.
Параметр а
определяет положение центра нормальной
плотности,
-
разброс относительно центра.
Свойства нормального распределения:
Для нормального распределения совпадают величины математического ожидания, моды и медианы.
Кривая плотности нормального распределения симметрична относительно средней а.
Если постоянно , а меняется а, то форма кривой остается неизменной, а ее график смещается вдоль оси абсцисс.
При постоянстве а изменение влечет изменение ширины и высоты кривой.
Площадь под нормальной кривой не зависит от а и и всегда равна единице.
Вероятность попадания нормально распределенной величины в интервалы
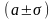 ,
,
 ,
,
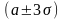 составляет 68.3%, 95.4% и 99.7% соответственно.
составляет 68.3%, 95.4% и 99.7% соответственно.
Нормальная кривая – это график плотности нормального распределения.
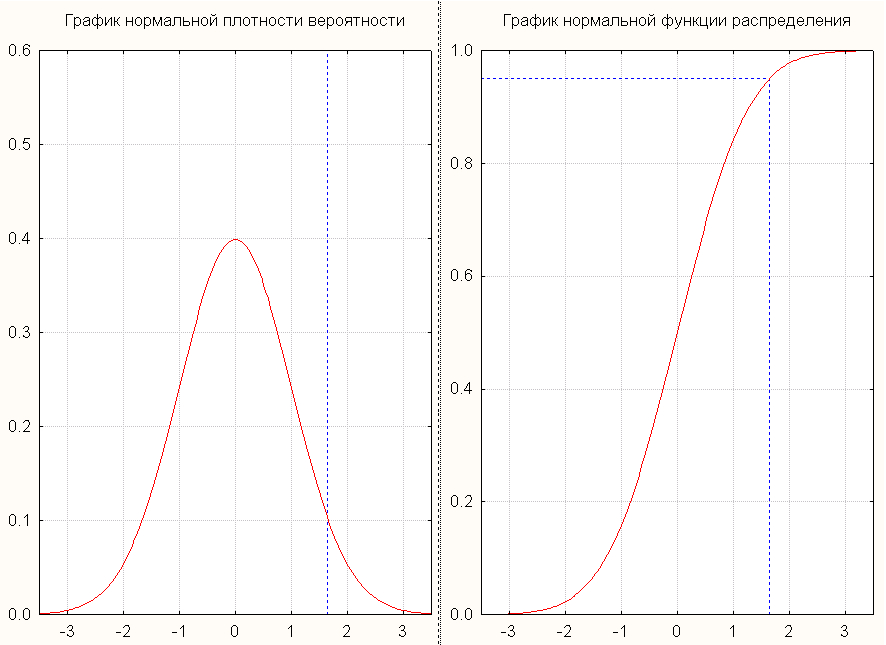
Р
95.4%
99.7%
ис 1. Графики функции плотности и функции распределения стандартного нормального законаПоказательное распределение (экспоненциальное).
Это распределение непрерывной случайной величины. Положительная случайная величина Х имеет показательное распределение с параметром λ>0, если его плотность распределения задается функцией:
 (3.4), где
(3.4), где

Данное распределение имеет всего один неизвестный параметр λ. Математическое ожидание и дисперсия определяются соответственно:

Распределение «хи – квадрат»
Если случайные величины
 независимы и каждая из них имеет
стандартное нормализованное распределение
(параметры такого распределения:
математическое ожидание а=0, среднее
квадратичное отклонение
=1),
то случайная величина
независимы и каждая из них имеет
стандартное нормализованное распределение
(параметры такого распределения:
математическое ожидание а=0, среднее
квадратичное отклонение
=1),
то случайная величина
 определяется как:
определяется как:
 (3.5)
(3.5)
Данная
случайная величина имеет
 распределение
с n
степенями
свободы. Функция плотности хи-квадрат
распределения имеет вид:
распределение
с n
степенями
свободы. Функция плотности хи-квадрат
распределения имеет вид:
 ,
где
,
где
 ,
,
 -
гамма - функция.
-
гамма - функция.
Согласно основной теореме теории вероятностей о сходимости многих распределений к нормальному: распределение медленно стремится к нормальному с увеличением числа степеней свободы.
