2.2. Интерполяция по чебышевским узлам

Вернемся к изучавшейся в предыдущей главе задаче интерполяции.

Сравнивая конечноразностные интерполяционные многочлены,

построенные по системе равноотстоящих узлов, с интерполяционным многочленом Лагранжа, предполагающим произвольное расположение несовпадающих узлов на промежутке интерполирования [а, Ь], следует отметить, что первые более просты и удобны в использовании, вторые же обладают большими возможностями. Нет сомнений в том, что если можно располагать узлы в пределах отрезка [а, Ь] как угодно, то имеет смысл использовать большее количество точечной информации о функции там, где она более сильно изменяется. Особенно существенным это замечание может оказаться при эрмитовой интерполяции.

Подойдем к проблеме расположения узлов интерполяции с несколько иной стороны.

Желая, чтобы интерполяционный многочлен Лагранжа L_n(x) (1.6) в целом хорошо приближал функцию f(x) на отрезке [а, Ь], поставим вопрос: как расположить на нем и + 1 узлов интерполяции х_; (г = 0,1, ...,«), чтобы при этом минимизировать максимальную на [а, Ь] погрешность?

Поскольку, согласно (1.15),

Как' видим, фактическая максимальная разность и ее оценка ро формуле (2.10) на функции f(x) = P_n+\(x) совпали, значит, Оценка (2.10) достижима, т.е. правая часть ее в общем случае не может быть уменьшена.

2.3. О многочленах наилучших равномерных приближений

Резюмируя исследования предыдущего параграфа, в частности, анализируя неравенство (2.10), можно хотя бы частично ответить на вопрос о сходимости последовательности интерполяционных многочленов Лагранжа L_n(x) к функции /(*), для которой они построены:

если функция f(x) бесконечно дифференцируема на [а, Ь] и в качестве узлов интерполяции берутся корни многочленов Чебышева (приведенные к отрезку [<я, Ь]), то

max \f(x)-L_n(xi——>0.

узлов интерполяции последовательность интерполяционных многочленов Лагранжа (L_n(x)) (построенных по точным значениям функции /(*)) сходится к f{x) по норме Чебышева; другими словами, имеет место равномерная сходимость последовательности (L_n(x))к f{x).

Обобщением установленного факта для непрерывных (не обязательно дифференцируемых) функций и произвольных (не обязательно интерполяционных) многочленов является широко известная в математическом анализе теорема.

Теорема 2.1 (Вейерштрасса) [5, 29, 64, 87, 102]. Для любой непрерывной на [я, Ь] функции f{x) найдется такой многочлен Q_n{x), что

\f(x)-Q_n(x)i<e Vs>0 \/хе[а,Ь].

Как следует из теоремы Вейерштрасса, если отказаться от того, чтобы аппроксимирующий функцию f(x) многочлен Q_n (χ) степени η был интерполяционным, от f{x) достаточно потребовать непрерывность на [а, Ъ\, чтобы за счет повышения степени многочдена при надлежащем подборе его коэффициентов величина чебышевской нормы ||/(x)-£?_w(*)||cT_a ь\ могла быть сделанной сколь угодно малой, иначе, чтобы качество аппроксимации функции f(x) многочленом Q_n{x) на отрезке [а, Ь] было сколь угодно хорошим в смысле чебышевской метрики.

Если степень η аппроксимирующего f(x) многочлена Q_n(x) зафиксировать и распоряжаться только его коэффициентами, то в общем случае величину ||/(jc)-g_n(x^|_cr ^ нельзя сделать сколь угодно малой. Однако доказано [28, 40], что для любой функции f(x)eС[а, Ь] существует единственный такой

многочлен ζ)ζ (χ), который из всех многочленов Q_n {χ) степени η наилучшим образом аппроксимирует на [а, Ь] функцию /(χ), минимизируя максимальное расстояние между f(x) и Q_n(x). Этот

многочлен, т.е. многочлен Ql (x), такой, что

называется многочленом наилучшего равномерного приближения для f{x) на [а, Ь] или ее чебышевским приближением^. Для последовательности величин

представляющих собой погрешности аппроксимации функции f(x) е С[а, Ь] посредством многочлена Ql (χ) , в соответствии с теоремой Вейерштрасса можно установить монотонную сходимость к нулю, т. е. что

Одним из характеристических свойств многочленов наилучших равномерных приближений является критерий Чебышева. Его отражает следующая теорема.

Теорема 2.2 (Чебышева). Многочлен Qi(x) является многочленом наилучшего равномерного приближения для функции fix) € С[а, Ь] тогда и только тогда, когда на [я, Ь] существует не менее η+ 2 таких точек x_it что в них поочередно принимаются наибольшие положительные и отрицательные отклонения, т. е. поочередно разность

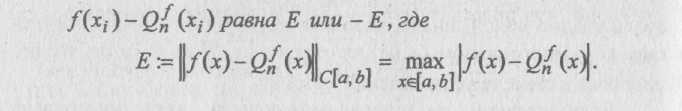
Эта теорема (доказательство которой можно найти, например, в [5, 10, 13, 40, 102]) говорит о том, что максимальная ошибка аппроксимации функции многочленом наилучшего равномерного приближения реализуется в числе точек большем, по меньшей мере, на 2, чем степень многочлена, причем знаки ошибки чередуются. Точки x_it в которых реализуется максимальное

отклонение многочлена Q^ix) от f(x) на [я, Ь], называются точками чебышевского альтернанса.

' Первое доказательство существования многочлена наилучшего равномерного приближения для произвольной непрерывной функции дано французским математиком Э. Борелем (1871-1956).

К сожалению, неизвестны ни общий вид многочленов наилучших равномерных приближений, ни способы их построения. Имеются лишь некоторые методики построения многочленов, близких к наилучшим равномерным (см., например, [13, 37, 40, 83, 90]), а также способы построения чебышевских приближений невысокого порядка для нескольких весьма узких классов функций. Последние существенно опираются на приведенную теорему о чебышевском альтернансе, что демонстрируется в следующих двух простейших случаях.

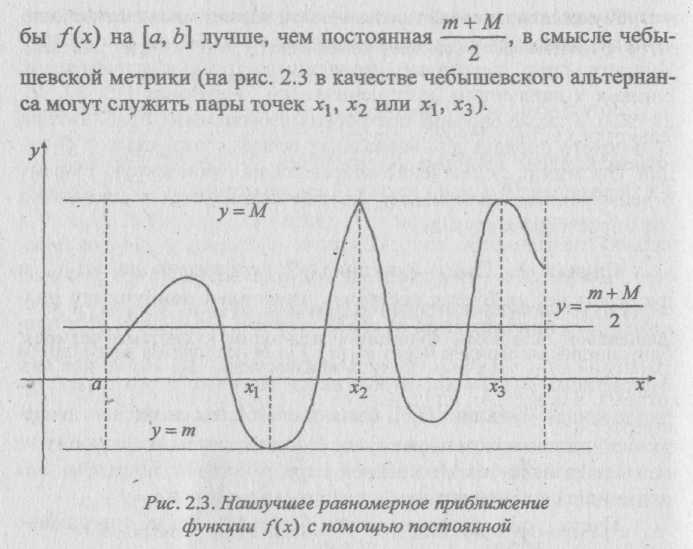
Случай А. Пусть функция/(л:) непрерывна на [а, Ь], и пусть для нее требуется построить многочлен наилучшего равномерного приближения нулевой степени. Обозначим этот приближающий многочлен через ^оС*)· Он определяется всего одним параметром: <p_o(x) = Aq. Чтобы найти значение этого параметра для заданной функции /(*), воспользуемся тем свойством непрерывной на замкнутом промежутке функции, согласно которому на нем всегда найдутся, по крайней мере, две точки, в которых она принимает свои наименьшее и наибольшее значения.

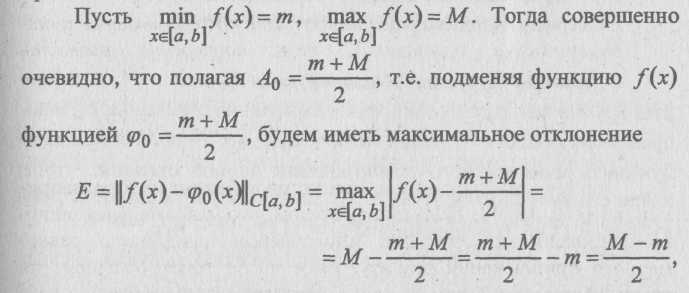
причем точки отрезка [д, Ь], в которых оно реализуется, — это точки, где принимаются значения тиМ.В силу непрерывности /(*), локальные минимумы и максимумы должны чередоваться; по меньшей мере, два из них определяют точки чебышевского

Случай Б. Пусть аппроксимируемая функция f(x) дифференцируема и выпукла (в широком смысле) на отрезке [я, Ь], а аппроксимирующая ее функция φ(χ) = Aq + Αγχ — многочлен наилучшего равномерного приближения первой степени. Чтобы найти его коэффициенты Aq и А\, следует изучить разность между f(x) и φ(χ)> т. е. функцию и(х):= /(*)- Aq - Αχχ.

Так как функция f(x) по предположению выпукла, а сдвиг на линейную функцию Α^ + Αγχ не изменяет выпуклости, то и функция и(х) выпукла на [а, Ь]. Если речь идет о выпуклости вниз, то, как известно из анализа выпуклых функций, выпуклость и(х) на [а, Ь] влечет ее унимодальность на этом отрезке, т.е. существует единственная точка с е[а,Ь], в которой и(х) имеет минимум; если и{х) выпукла вверх, то в точке с должен быть максимум и(х). В любом случае, точка се [а, Ь] есть точка

экстремума и(х), и за счет возможности варьирования коэффициентов функции φ(χ) (точнее, коэффициента Αγ) можно считать, что точка с является внутренней точкой отрезка [а, Ь].

Потребуем, чтобы точки а, с и Ъ в указанной последовательности составляли чебышевский альтернанс, т.е. чтобы в них последовательно принимались значения Е, - Ε, Ε или - Ε, Ε,

максимальная погрешность аппроксимации функции f(x) функцией φ{χ). Добавляя к этим требованиям еще необходимое условие экстремума дифференцируемой функции и(х) в точке с и возвращаясь к исходным функциям, приходим к системе четырех уравнений относительно четырех неизвестных А§, А\_% Ε и с (из которых, в основном, лишь первые три неизвестные представляют интерес):

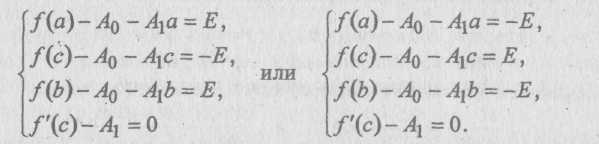
ем

а из четвертого следует А\ = /'(с), что говорит о параллельности хорды, стягивающей концы дуги графика f(x) на [a, h\, касательной, проведенной к /(*) во внутренней точке альтернанса, и аппроксимирующей f(x) прямой у = А_о + Αιχ (рис. 2.4).

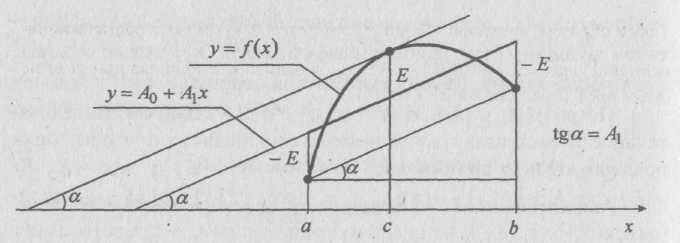
Рис. 2.4. Наилучшая Линейная аппроксимация дифференцируемой выпуклой функции

Пример 2.1. Построим многочлены наилучшего равномерного приближения нулевой и первой степеней для функции j = sinjc на отрезке [0, π/6].

Сразу заметим, что данная функция всюду дифференцируема (а значит, непрерывна) и выпукла вверх на заданном отрезке. При этом

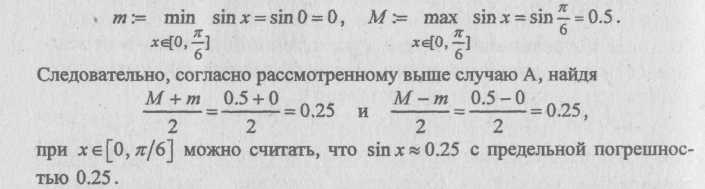
Далее, в соответствии со случаем Б, продифференцировав данную функцию, составляем систему: