МНОГОЧЛЕНЫ ЧЕБЫШЕВА И НАИЛУЧШИЕ РАВНОМЕРНЫЕ ПРИБЛИЖЕНИЯ

Дается определение многочленов Чебышева первого рода и изучаются их свойства. Показывается, что погрешность интерполирования гладкой функции многочленом фиксированной степени будет наименьшей, когда в качестве узлов интерполяции, используются корни многочленов Чебышева. Приводится (без доказательства) теорема о чебышевском альтернате, служащая , теоретической основой построения наилучших равномерных приближений, и рассматриваются простейшие ситуации, когда такие многочлены могут быть построены. Обсуждается идея использования разложения функций в степенные ряды для получения многочленов, близких к многочленам наилучших равномерных приближений.

2.1. Определение и свойства многочленов Чебышева

Определение 2.1. Многочленом Чебышева ' называется функция

Прежде всего убедимся, что функция Т_п(х), представленная с помощью тригонометрических функций, на самом деле является многочленом при любом и = 0,1, 2,....

Непосредственной подстановкой в (2.1) значений п = 0 и и = 1 получаем Tq (χ) = 1, 7j (x) = χ.

' Чебышёв Пафнутий Львович (1821-1894) — знаменитый русский математик. Его работы о многочленах наилучшего равномерного приближения легли в основу конструктивной теории функций. Стандартное обозначение Т„(х) можно соотнести с немецким написанием фамилии Tschebyschew.

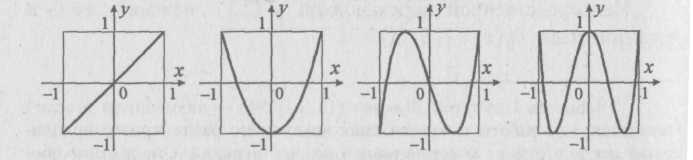
Рис. 1.1. Графики многочленов 7^ (jc) , Tjipi), Т$(х) и Т^{х)

Анализ рекуррентной формулы (2.2) позволяет считать очевидными следующие факты:

1. все функции Т_п(х), определенные в (2.1), являются многочленами при любом натуральном η;

1. степени этих многочленов возрастают с увеличением η,

причем старший член многочлена Т_п(х) равен 2^п~ х"\

3) многочлены Т„ (х) при четных η выражаются через степенные функции только четных степеней, при нечетных — только нечетных.

Наряду с многочленами Чебышева Т„(х) часто используют многочлены, получаемые из Т„ (х) делением на старший коэффициент, т.е.

— многочлены со старшим коэффициентом 1. Будем называть их нормированными многочленами Чебышева.

Многочлены Чебышева обладают рядом замечательных свойств. Рассмотрим некоторые их свойства, имеющие отношение к поставленной выше проблеме аппроксимации функций.

Свойство 2.1. Многочлен Чебышева Т_п(х) (а значит, и многочлен Т_п(х)) имеет на отрезке [—1,1] ровно η различных действительных корней; все они задаются формулой

Доказательство. Корни многочлена Чебышева Т_п(х) можно получить, решая тригонометрическое уравнение

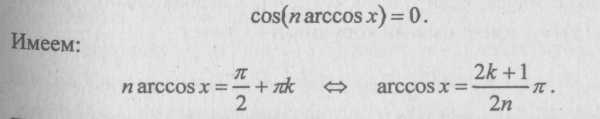
Поскольку главные значения арккосинуса должны принадлежать промежутку [0, π], целая переменная к здесь должна принимать значения от 0 до η -1. Переходя на этом промежутке к обратной

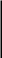
функции, иначе, беря косинус от левой и правой частей последнего равенства и учитывая, что cos arccosχ = χ, приходим к выводу, что я действительных корней многочлена Т_п{х), определяемые формулой (2.3), на самом деле существуют. Их несовпадение и принадлежность отрезку [-1,1] следует из того, что они суть значения косинуса, соответствующие различным значениям его аргумента, расположенным на промежутке его монотонности.

Свойство 2.2. Корни многочленов Чебышева перемежаются с точками их наибольших и наименьших значе-

нив это с (2.3). Факт чередования максимумов и минимумов у Т„ (х) следует из того, что значения выражения η arccos x в точках Xj, согласно промежуточному равенству и arccos χ = π j, равны поочередно 0, π, 2π, 3π,..., и потому, в зависимости от четности j, значения cos(« arccos χ) будут соответственно то +1, то -1.

Свойство 2.3 (теорема Чебышева). Из всех многочленов степени η со старшим коэффициентом 1 нормированный многочлен Чебышева Т_п(х) наименее уклоняется от нуля на отрезке [-1,1].

этих прямых (по свойству 2.2), а график Р_п (х) при д; е [-1,1] должен лежать строго внутри этой полосы (по предположению), то можно утверждать, что многочлен-разность Q_n__x (x) в точках экстремумов jc,=cos—π должен иметь определенные знаки: «+» ⁷ η

при четных j и «-» при нечетных j (рис. 2.2).

Поскольку Т_п (х) на [-1,1] имеет η +1 таких точек экстремумов, следовательно, многочлен Q_n-\(x) должен иметь, по меньшей мере, η перемен знаков, т.е. η корней, что противоречит следствию из основной теоремы алгебры многочленов. Полученное противоречие говорит о несостоятельности сделанного в начале доказательства предположения.

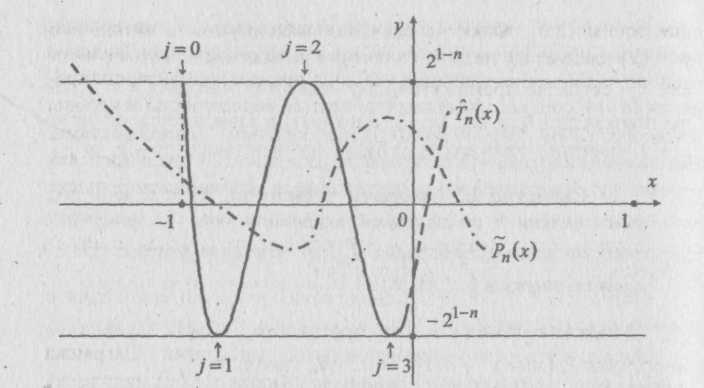
Рис. 2.2. Возможное совместное поведение графиков f_n{x) и Р„(х)

Только что доказанное свойство означает, что среди всех многочленов степени η вида

именно нормированный многочлен Чебышева Т_п ух) минимизирует максимальное расстояние от графика многочлена при хе[-1,1] до оси абсцисс, т.е. Т_п(х) — это многочлен с наименьшей нормой (так называемой чебышевской нормой) на множестве многочленов вида (2.6) в пространстве С[—1,1].

Замечание 2.1. Иногда бывает более удобным использовать смещенные многочлены Чебышева Т*{х), которые определяются на отрезке [0,1] и могут быть получены из классических многочленов Чебышева Т„(х) заменой в них аргумента χ на аргумент 2х-\.