
- •Некоторые теоретические сведения. Множества Основные сведения
- •Связь между (не)совместностью и (не)зависимостью
- •Формулы полной вероятности и байеса
- •Биномиальное распределение
- •Наивероятнейшее число событий
- •Простые однородные цепи маркова
- •Распределение пуассона
- •Теоремы муавра – лапласа
- •Локальная теорема Муавра – Лапласа
- •Интегральная теорема Муавра – Лапласа
- •Общие критерии применимости
- •Отклонение относительной частоты от вероятности в схеме Бернулли
- •Одномерные случайные величины Функция распределения
- •Дискретные одномерные св
Теоремы муавра – лапласа
Теоремы Лапласа представляют собой другой случай приближения биномиального распределения. Они дают удовлетворительное приближение при значениях p, близких к 0,5. Формулы аппроксимируют значения биномиального распределения нормальным (гауссовым) распределением:

Локальная теорема Муавра – Лапласа
Рассмотрим другой случай приближения биномиального распределения:

Здесь
 – функция Гаусса, табулированная и
нормированная (эти два свойства так же
объединяют термином «стандартизированная»).
Её значения можно как найти с помощью
таблиц значений, так и непосредственно
посчитав с помощью компьютера (например,
с помощью САПР Mathcad) или
даже вручную.
– чётная функция:
– функция Гаусса, табулированная и
нормированная (эти два свойства так же
объединяют термином «стандартизированная»).
Её значения можно как найти с помощью
таблиц значений, так и непосредственно
посчитав с помощью компьютера (например,
с помощью САПР Mathcad) или
даже вручную.
– чётная функция:
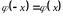 .
.
Локальная формула применяется для вычислений значений в точке (ровно m успехов).
Интегральная теорема Муавра – Лапласа

где
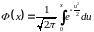 – стандартизированная функция Лапласа.
Её значения уже нельзя найти вручную,
поскольку интеграл не вычисляется
аналитически, а только численно.
– стандартизированная функция Лапласа.
Её значения уже нельзя найти вручную,
поскольку интеграл не вычисляется
аналитически, а только численно.
 – нечётная функция:
– нечётная функция:
 .
.
Интегральная формула применяется для вычислений значений на интервале.
Общие критерии применимости
Сформулируем общие критерии выбора типа приближения в данном случае.
Если n мало, то следует считать по формуле Бернулли, так как в этом случае оба приближения будут неточными, а вычисление
 не представляет значительных сложностей.
не представляет значительных сложностей.Если 0,1 < p < 0,9 и npq > 9, то целесообразно пользоваться формулами Муавра – Лапласа.
Если p > 0,1 или p > 0,9, npq ≤ 9, то следует пользоваться формулой Пуассона.
В остальных случаях приходится выбирать. В случае интервала, как правило, предпочитают интегральную формулу Муавра – Лапласа ввиду того, что не нужно вычислять сумму ряда, как в случае формулы Пуассона. При очень больших n оба приближения дают удовлетворительные результаты.
Отклонение относительной частоты от вероятности в схеме Бернулли

Может
потребоваться найти не только саму
вероятность P, но и границу
симметричного интервала ε,
в который заключена частота с наперёд
заданной вероятностью. В этом случае
потребуется найти
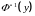 ,
то есть при заданном y
найти такое x, что
,
то есть при заданном y
найти такое x, что
 .
Число успехов m будет
принадлежать следующему интервалу:
.
Число успехов m будет
принадлежать следующему интервалу:

Одномерные случайные величины Функция распределения
Функция
распределения (ФР) случайной величины
(СВ) ξ – это функция, характеризующая
распределение СВ (скаляра в одномерном
случае и вектора – в многомерном):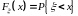 .
Далее для простоты примем
.
Далее для простоты примем
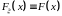 .
.
Свойства ФР:
 ;
;монотонное неубывание:
 ;
;непрерывность слева:
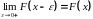 ;
;
существует взаимно-однозначное соответствие между распределением СВ и её ФР.
Замечания
ФР или непрерывна в точке, или содержит разрыв первого рода.
В зарубежной литературе встречается другое определение ФР:
 .
Это ничего не изменит в наших рассуждениях,
кроме очевидного изменения в свойствах,
так как в этом случае ФР станет
непрерывной справа.
.
Это ничего не изменит в наших рассуждениях,
кроме очевидного изменения в свойствах,
так как в этом случае ФР станет
непрерывной справа.
Дискретные одномерные св
В
дискретном одномерном случае
 .
График функции представляет собой набор
ступенек, в общем случае разной длины
и разной высоты.
.
График функции представляет собой набор
ступенек, в общем случае разной длины
и разной высоты.

