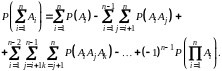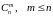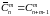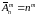Некоторые теоретические сведения. Множества Основные сведения

В математике встречаются разнообразные множества. Можно говорить о множестве граней многогранника, точек на прямой, множестве натуральных чисел и т. д. Понятие множества настолько общее, что трудно дать какое-либо определение, которое не сводилось бы просто к замене слова «множество» его синонимами: совокупность, собрание элементов и т. п.

Основные обозначения:

• – множества (прописные латинские буквы);

• – элементы множеств (строчные латинские буквы);

• – принадлежность, непринадлежность элемента множеству;

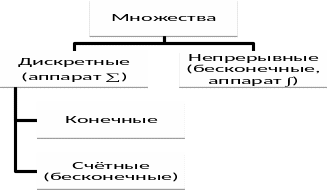
• – вложенность множества 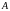в множество ;

• – равенство (эквивалентность) множеств (когда и );

• – мощность (число элементов) множества;

• – пустое множество (не содержит ни одного элемента), единственно;

• – универсальное множество, универсум (содержит все элементы какой-либо категории), единственно.

Основные операции над множествами

Объединение (сумма)

Это множество элементов, принадлежащих хотя бы одному объединяемому множеству (или одному, или другому, или обоим сразу). Сумма двух множеств: 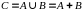( или ); обобщение: .

Пересечение (произведение)

Это множество элементов, принадлежащих всем пересекаемым множествам одновременно. Произведение двух множеств: 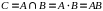( и ); обобщение: .

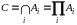Отрицание

Это множество элементов, не принадлежащих отрицаемому: .

Эти три операции являются базисными, то есть через них выражаются все другие операции. В качестве примера рассмотрим ещё одну часто употребляемую операцию.

Дополнение (разность)

Это множество элементов, принадлежащих уменьшаемому множеству, но не принадлежащих вычитаемому: ( без ).

Выразим разность через базисные операции: .

Далее будем пользоваться алгебраическими терминами и обозначениями (сумма, произведение, разность), помня о том, что мы производим операции именно над множествами. Отметим, что аналогично со стандартными операциями, приоритет операции произведения над множествами выше, чем у сложения и вычитания.

Свойства базисных операций

Для множеств применимы законы коммуникативности

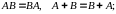
ассоциативности

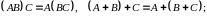
и дистрибутивности

Так же имеют место очевидные равенства:

Равенства Де Моргана

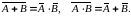
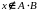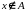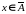Доказательство. Докажем 2-е равенство Де Моргана (1-е доказывается аналогично). Пусть . Тогда , то есть либо , либо , либо ни тому, ни другому. Но если , то , а если , то . Следовательно, в любом случае , то есть .

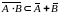Наоборот, пусть . Тогда либо , либо , либо 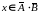. Если , то , а если , то . Таким образом, в любом случае , то есть , откуда следует .

Приложение теории множеств к теории вероятностей

В теории вероятностей роль множеств играют случайные события (случаи), а роль универсального множества – множество всех элементарных событий или пространство элементарных событий (ПЭС) . Событие – подмножество . Оно наступает тогда, когда результатом опыта является одно из элементарных событий .

называют ещё достоверным событием, а – невозможным.

Комбинаторика

Выборки	Без возвращения	С возвращением
Неупорядоченная
Упорядоченная

Иногда используются обозначения

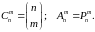
Перестановки – частный случай упорядоченной выборки без возвращения:

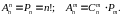
Некоторые свойства сочетаний:

гипергеометрическое распределение

Пусть имеется множество из N дискретных элементов. Из них M элементов обладают нужным нам свойством, а остальные – нет. Случайным образом из множества выбираются n элементов. Требуется найти вероятность того, что в выборке будут ровно m элементов с нужным свойством.

Вероятности подобных выборок реализуются случайной величиной, имеющей гипергеометрическое распределение.

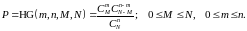
геометрические вероятности

Вероятность события при непрерывном множестве элементарных событий называется геометрической вероятностью.

Размерность как общего, так и благоприятного числа исходов определяется количеством независимых случайных величин в задаче. Если такая величина одна, то вероятность будет определяться отношением длин, если две – то площадей, если три – объёмов, и т. д.

классификация и свойства событий

Условная вероятность – вероятность одного события при условии, что другое событие уже произошло.

То, что стоит справа от вертикальной черты – свершившийся факт!

События независимы (по вероятности), если Для независимых событий: . Наступление одного события не влияет на наступление других событий.

Иначе, если равенство не выполняется, – события зависимы. Общая формула вероятности произведений событий:

События несовместны, если наступление одного события исключает возможность наступления других: 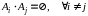. Такие случайные события не могут произойти вместе, одновременно. Для несовместных событий

Иначе события совместны. Общая формула вероятности суммы событий: