1.3.1 Метод узловых напряжений

Метод узловых напряжений широко применяется для расчета электрических цепей, в частности в различных программах автоматизированного проектирования электронных схем. Метод узловых напряжений базируется на ЗТК и законе Ома. Он позволяет снизить число решаемых уравнений до величины, равной n_у–1. В основе этого метода лежит расчет напряжений в (n_у–1)-м узле цепи относительно базисного узла. После этого на основании закона Ома находятся токи или напряжения на соответствующих ветвях. Рассмотрим сущность метода узловых напряжений на примере резистивной цепи, изображенной на рисунке 1.8 а.

1) Примем потенциал V₃ = 0 (базисный узел) и преобразуем источники напряжения в эквивалентные источники тока (рисунок 1.7 б), где i_г1 = u_г1G₁; i_Г2 = u_Г2G₂; i_Г3 = u_Г3G₃; G₁ = 1/R₁; G₂ = 1/R₂; G₃ = 1/R₃; G₄ = 1/R₄; G₅ = 1/R₅.

2) Составим уравнения для узлов 1 и 2 по ЗТК: –i₁ + i₂ – i₄ + i₅ = 0 ; i₄ + i₃ – i₂ = 0.

3) Каждый из этих токов можно выразить через узловые напряжения и токи i_Г1, i_Г2, i_Г3:

i₁ = i_Г1 – u₁G₁ ; i₂ = i_Г2 – (u₂ – u₁)G₂ ; i₃ = i_Г3 + u₂G₃ ; i₄ = (u₂ – u₁)G₄ ; i₅ = u₁G₅ . (1.32)

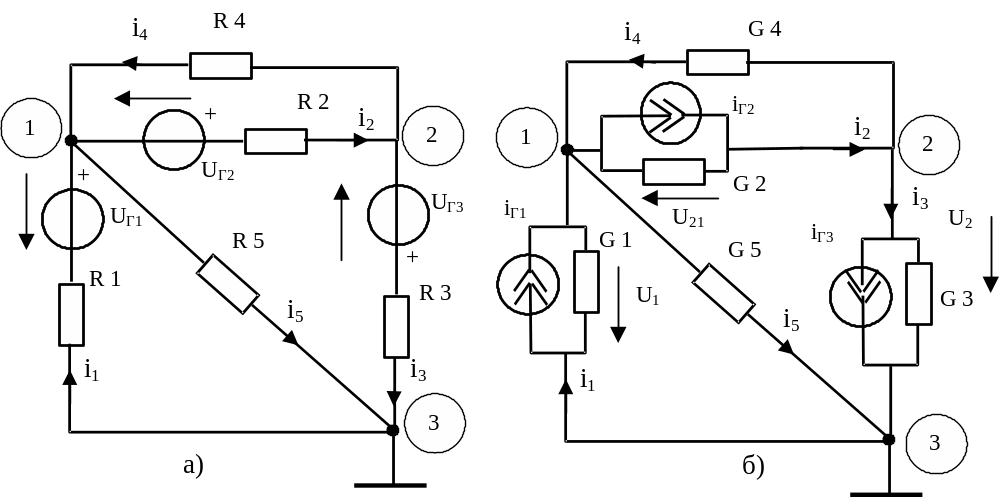
Рисунок 1.7 – Расчёт схем по методу узловых напряжений

4) Подставив эти значения в уравнения для узлов, получим после группировки членов при u₁, и₂ и переносе i_г1, i_г2, i_г3 в правую часть:

(G₁ + G₂ +G₄ + G₅)u₁ – (G₂ + G₄)u₂ = i_г1 – i_г2 ; (1.33)

–(G₂ + G₄)u₁ + (G₂ + G₃ + G₄)u₂ = i_г2 – i_г3 . (1.34)

5) Введем следующие обозначения:

(G₁ + G₂ +G₄ + G₅) = G₁₁; (G₂ + G₃ + G₄) = G₂₂; (G₂ + G₄) = G₁₂ = G₂₁; (1.35)

i_г1 – i_г2 = i_у1 ; i_г2 – i_г3 = i_у2. (1.36)

Тогда получим систему уравнений:

G₁₁u₁ – G₁₂u₂ = i_у1; (1.37)

–G₂₁u₁ + G₂₂u₂ = i_у2. (1.38)

Проводимости G₁₁ и G₂₂ представляют собой арифметическую сумму проводимостей всех ветвей, подсоединенных соответственно к узлам 1 и 2, они называются собственными проводимостями узлов 1 и 2. Проводимости G₁₂ = G₂₁ определяются арифметической суммой проводимостей всех ветвей, включенных между узлами 1 и 2, и называются взаимными проводимостями узлов 1 и 2. Алгебраическую сумму задающих токов i_у1 и i_у2 источников тока, подключенных соответственно к узлам 1 и 2, называют задающими узловыми токами узлов 1 и 2.

6) Решив систему относительно и₁ и u₂, определим узловые напряжения цепи. Искомые токи находим по закону Ома.

Полученный результат можно обобщить на произвольную резистивную схему с п узлами. Система уравнений по методу узловых напряжений будет иметь вид:

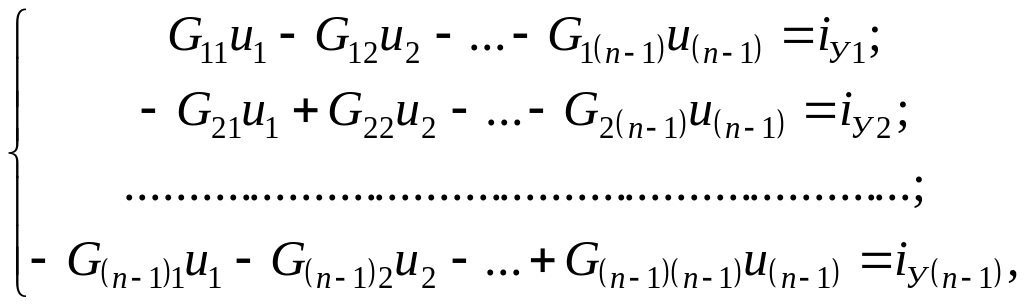(1.39)

где i_у1, i_у2, ..., i_у(n-1) – задающие узловые токи в узлах 1, 2, ..., (n – 1).

1.3.2 Метод эквивалентного генератора

Метод эквивалентного генератора используется в случае, когда необходимо найти ток, напряжение или мощность в одной ветви. При этом удобно всю остальную часть цепи, к которой подключена данная ветвь, рассматривать в виде двухполюсника [2]. Двухполюсник называют активным, если он содержит источники электрической энергии, и пассивным – в противном случае. На рисунках активный двухполюсник будем обозначать буквой А, а пассивный – П. Различают две модификации метода эквивалентного генератора: метод эквивалентного источника напряжения и метод эквивалентного источника тока.

Метод эквивалентного источника напряжения. Этот метод базируется на теореме Тевенина, согласно которой ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником (генератором) напряжения с задающим напряжением, равным напряжению холостого хода на зажимах разомкнутой ветви, и внутренним сопротивлением, равным эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви (рисунок 1.8).

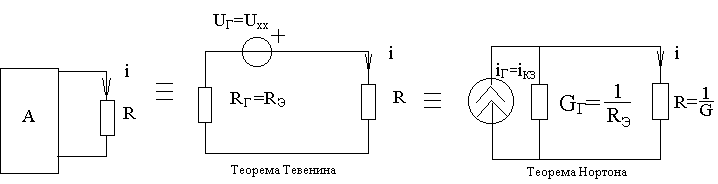
Рисунок 1.8 – Суть теорем Тевенина и Нортона

После замены активного двухполюсника эквивалентным источником на рисунке 1.8 в соответствии с этой схемой имеем:

i = u_xx/(R + R_э) , (1.40)

где R_э можно найти либо экспериментальным, либо расчетным путем.

Метод эквивалентного источника тока. В основе этого метода лежит теорема Нортона, согласно которой ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником тока с задающим током, равным току короткого замыкания этой ветви, и внутренней проводимостью, равной эквивалентной входной проводимости со стороны разомкнутой ветви (рисунок 1.8, в).

Искомый ток можно найти по формуле: i = i_кз[R_э/(R + R_э)].

Очевидно, что методы эквивалентного источника как напряжения, так и тока дают один и тот же результат. Применение того или иного метода определяется удобством и простотой нахождения u_хх или i_кз.