1.8.2 Параллельный колебательный контур и резонанс токов

Простейший параллельный колебательный контур с потерями в ветвях R₁ и R₂ имеет вид, изображенный на рисунке 1.21, а.

Комплексная входная проводимость такого контура:

Y = + = G₁ + G₂ – j(B₁ – B₂) = G – jB, (1.93)

где = G₁ – jB₁; = G₂ – jB₂ – комплексные проводимости ветвей с индуктивностью и емкостью соответственно.

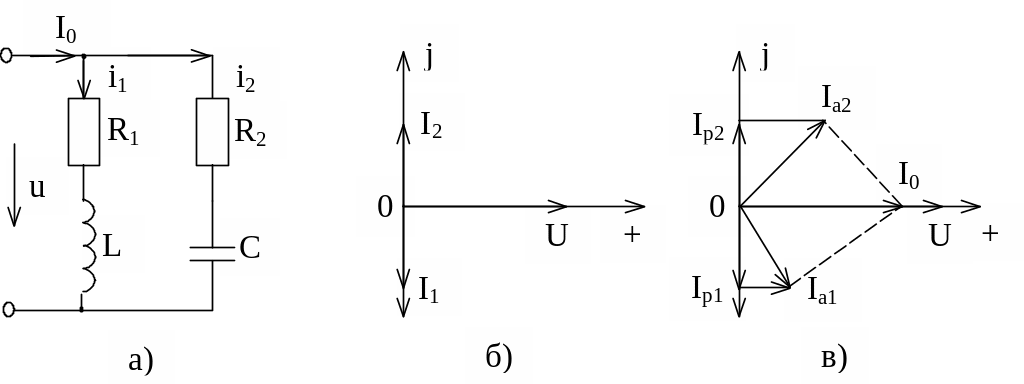
Рисунок 1.21 – Параллельный колебательный контур с потерями

и векторные диаграммы

Из условия резонанса токов имеем  = arctg(B/G) = 0. Отсюда следует:

B = B₁ – B₂ = {L/[R₁² + (L)²]} – {(1/C)/[R₂² + (1/C)²]} = 0. (1.94)

Решив (1.94) относительно  , получим уравнение резонансной частоты

. (1.95)

Резонанс в параллельном контуре возможен лишь в случае неотрицательности подкоренного выражения (т. е. при R₁ <  и R₂ <  или R₁ >  и R₂ >  ).

Реактивные составляющие токов в ветвях при резонансе равны друг другу:

I_p1 = UB₁ = I_p2 = UB₂. (1.96)

При этом ток в неразветвленной части цепи определяется из уравнения:

i₀ = U/R_0э , (1.97)

где активное сопротивление R_0э называют эквивалентным резонансным сопротивлением параллельного контура.

Входной ток контура совпадает по фазе с приложенным напряжением. Величину R_0э можно найти из условия резонанса токов. При резонансе токов В = 0, а эквивалентное резонансное сопротивление контура равно:

R_0э = ( ² + R₁R₂)/(R₁ + R₂) . (1.98)

Контур без потерь. Для контура без потерь (R₁ = R₂ = 0) уравнение резонансной частоты принимает вид:

_р = ₀ = 1/ , (1.99)

т. е. совпадает с выражением для последовательного контура. Эквивалентное сопротивление контура без потерь R_0э =  и входной ток равен нулю, а добротность обращается в бесконечность.

Контур с малыми потерями. (R₁ <<  ; R₂ <<  ). Резонансная частота для этого случая будет приближенно совпадать с частотой ₀. Для контура с малыми потерями можно принять, что ² >> R₁R₂, тогда:

R_0э   ²/(R₁ + R₂) =  ²/R = Q²R, (1.100)

где R = R₁ + R₂. Ток в неразветвленной части цепи: I₀ = U/R_0э = U/(Q²R), а действующие значения токов в ветвях:

I₁ = I₂ = U/ = U/(QR). (1.101)

Отношение токов в ветвях к току в неразветвленной части цепи равно добротности контура: I₁/I₀ = I₂/I₀ = Q, т. е. ток в реактивных элементах L и С при резонансе в Q раз больше тока на входе контура (отсюда термин «резонанс токов»). На рисунке 1.21, в изображена векторная диаграмма токов для этого случая.

При R₁ = R₂ =  для _р получаем неопределенность, при этом входное сопротивление контура будет носить чисто активный характер на любой частоте (случай безразличного резонанса).

Частотные зависимости параметров параллельного контура без потерь от частоты имеют вид:

B_L() = 1/(L); B_C() = C; B() = (1/L) – C; X() = 1/B() . (1.102)

На рисунке 1.22 изображены графики этих зависимостей. Из рисунка следует: при  < ₀ входное сопротивление контура Х носит индуктивный, а при  > ₀ – ёмкостной характер, причём вследствие отсутствия потерь при переходе через частоту  = ₀ ФЧХ контура изменяется скачком от –/2 до /2, а входное реактивное сопротивление контура претерпевает разрыв (|Х| =  ). Комплексное эквивалентное сопротивление контура с малыми потерями можно определить уравнением:

. (1.103)

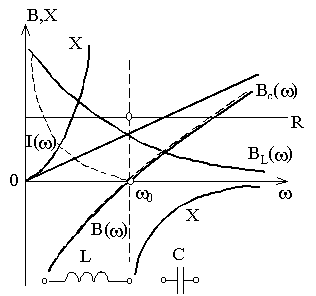
Рисунок 1.22 – Частотные зависимости параллельного контура без потерь

На рисунке 1.23 изображены нормированные относительно R_0э частотные характеристики R_э/R_0э, X_э/R_0э и Z_э/R_0э как функции обобщенной расстройки .

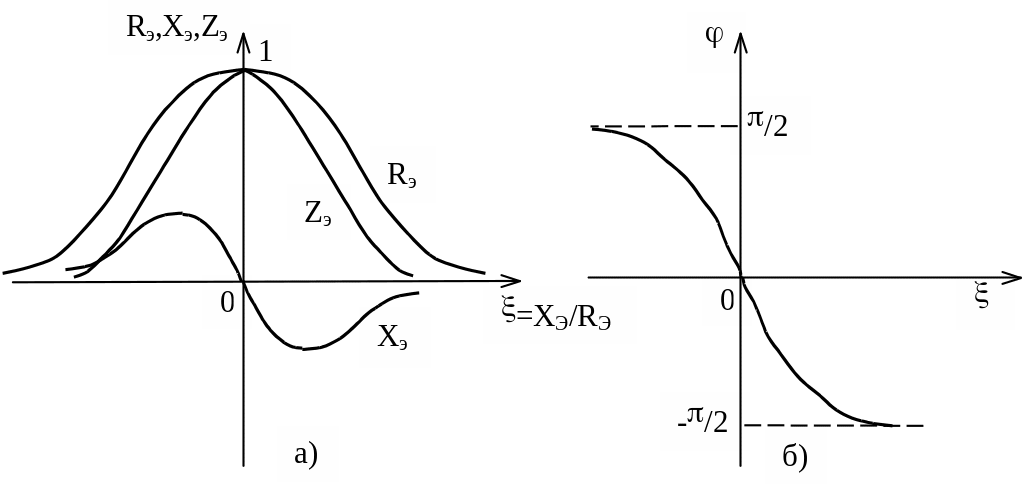
Рисунок 1.23 – Нормированные частотные характеристики

параллельного контура

Фазочастотная характеристика цепи определится уравнением:

 = –arctg(X_э/R_э) = –arctgx . (1.104)

Анализ полученных зависимостей показывает, что по своему виду частотные характеристики контура с потерями существенно отличаются от характеристик контура без потерь. Прежде всего, зависимости реактивного сопротивления контура от частоты: для контура с потерями при резонансе оно оказывается равным нулю, а в контуре без потерь терпит разрыв (рисунок 1.22).

Колебательный контур подключается обычно к источнику с задающим напряжением и определённым внутренним сопротивлением R_Г. При этом напряжение на контуре определяется:

. (1.105)

При резонансе токов: . (1.106)

Определяя частотную зависимость и вводя понятие эквивалентной добротности контура, которая определяется выражением

, (1.107)

могут быть получены АЧХ и ФЧХ относительно напряжения на контуре, нормированного к напряжению U_КР :

; . (1.108, 1.109)

На рисунке 1.24 показан характер этих зависимостей при различных сопротивлениях R_Г источника.

Рисунок 1.24 – Частотные характеристики параллельного контура

Полоса пропускания параллельного контура определяется как полоса частот, на границах которой напряжение на контуре уменьшается в раз относительно U_КР. Параллельный контур в общем случае имеет более широкую полосу, чем последовательный. И только при R_г =  их полосы пропускания будут равны. Таким образом, для улучшения избирательных свойств параллелью контура его необходимо возбуждать источником тока. Параллельный контур нельзя использовать для усиления напряжения, так как всегда U_к.р < U_г.