Метод оценки преимуществ альтернатив (prometee-метод) -переделать

Рис. 1

Рис. 2

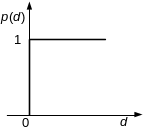
Обычный критерий

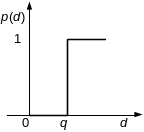
Воображаемый критерий

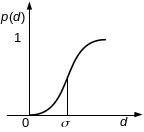
Критерий Гаусса

Критерий с линейным

преимуществом и областью

индифферентности

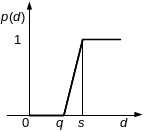
Ступенчатый критерий

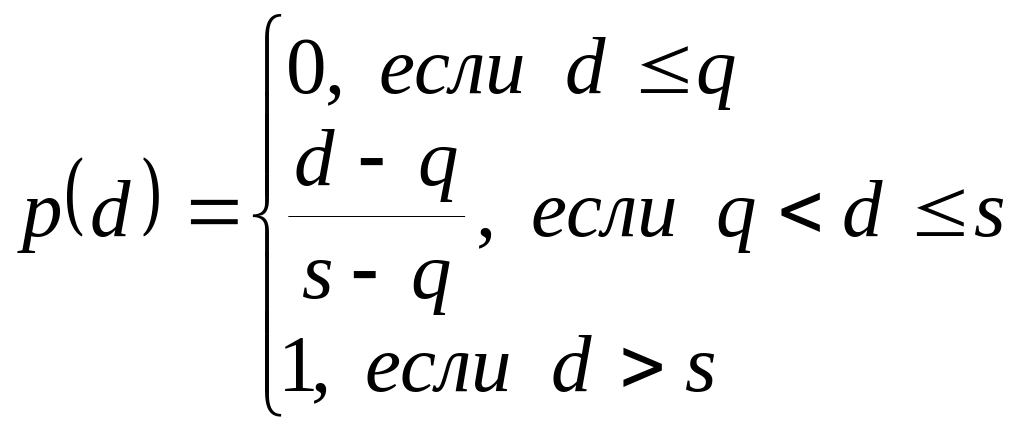
PROMETEE-метод относится к методам определения преимуществ одной альтернативы перед другой (Quatranking-методы). Приоритетность альтернатив описывают с помощью Quatranking-соотношения - Q_ij. Если представить проблему в виде , где - множество альтернатив, - количественное проявление альтернативы относительно критерия k. Для каждого критерия проводят парное сравнение всех альтернатив друг с другом, при этом рассчитывают разницу d_k между значениями и , по значению d_k определяют значение показателя приоритетности , где . Показатель приоритетности Î[0, 1] показывает, в какой степени альтернатива доминирует над альтернативой . Для d_k ≤ 0 присваивается значение = 0; при строгом преимуществе по отношению = 1, для Î[0, 1] значение показателя преимущества определяется величиной d_k. Привязка показателей преимущества к разнице d_k осуществляется с помощью функции приоритетности. Существует 6 типовых функций приоритетности, представляемых в виде обобщенных критериев (рис. 1). Обобщенный критерий может уточняться выбором относящихся к нему параметров (q, s, s). Функции приоритетности отражают приоритеты ЛПР относительно значений соответствующего критерия. При определении Quatranking-соотношения для каждой пары альтернатив по каждому критерию определяются два показателя приоритетности, характеризующие преимущество по отношению и по отношению (один из двух показателей всегда равен 0). Относительная значимость отдельных критериев k устанавливается с помощью факторов взвешивания w_k из условия .

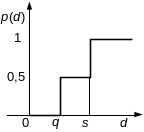
Критерий с линейным

преимуществом

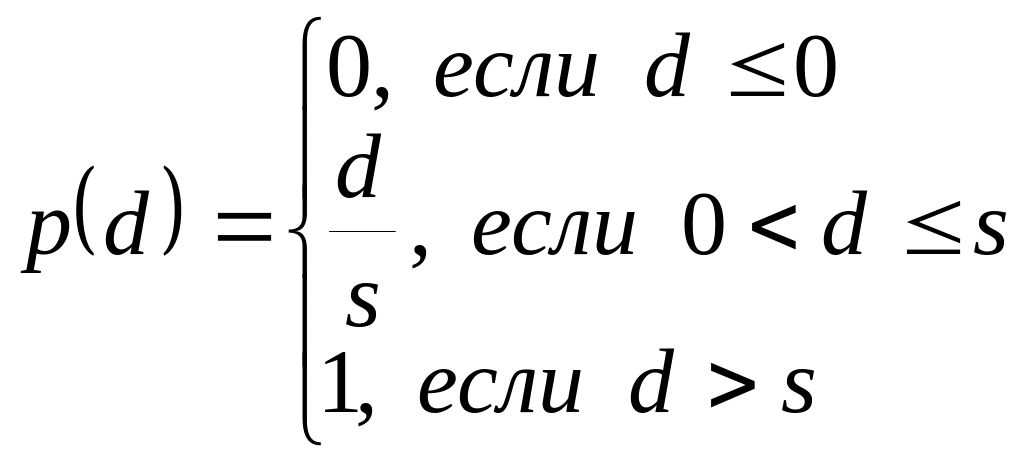
Для преимущества альтернативы по отношению к формируется Q_ij. в качестве средневзвешенного значения всех показателей приоритетности , относящихся критерию . Для целевых функций, стремящиеся к минимуму, значения показателей умножают на -1.

Пример.

Выберем альтернативу с помощью PROMETHEE-метода по четырем целевым критериям: РЗУ (размер земельного участка РЗУ, тыс. м²); ПП (потенциал персонала, чел.); ТЭФ (наличие транспортно-экспедиторских фирм, шт.); СНД (совокупный налог на доход, %) (табл. 1). Определим функции приоритетности (табл. 2).

Таблица 1. Основные показатели существенных признаков альтернатив

Альтернатива	РЗУ, м2	ПП, чел.	ТЭФ, шт.	СНД, %.
А1	60000	800	15	35
А2	42500	1100	12	25
А3	35000	1300	25	45
А4	35000	900	14	30
А5	40000	1000	17	40

Таблица 2. Обобщенные критерии и функции приоритетности целевых критериев

Целевой критерий	Обобщенный критерий и функции приоритетности
РЗУ	Воображаемый критерий, q = 5000 p1(d1) = 0, если d1 ≤ 5000 p1(d1) = 1, если d1 > 5000
ПП	Ступенчатый критерий, q = 50, s = 200 p2(d2) = 0, если d2 ≤ 50 p2(d2) = 0,5, если 50 < d2 ≤ 200 p2(d2) = 1, если d2 > 200
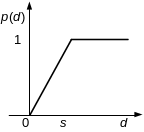
ТЭФ	Критерий с линейной функцией приоритетности и областью индифферентности; q = 1, s = 4 p3(d3) = 0, если d3 ≤ 1 p3(d3) = (d3 - 1) / 3, если 1 < d3 ≤ 4 p3(d3) = 1, если d3 > 4
СНД	Критерий с линейной функцией приоритетности; s = 100 p4(d4) = 0, если d4 ≤ 0 p4(d4) = d4 / 100, если 0 < d4 ≤ 100 p4(d4) = 1, если d4 > 100

Определим Quatranking-соотношение, для чего необходимо установить веса w_k. В нашем примере:

w₁ = 0,3; w₂ = 0,35; w₃ = 0,2; w₄ = 0,15:

.

Q(A₁,A₂) = 0,3p₁(A₁,A₂) + 0,35p₂(A₁,A₂) + 0,2p₃ (A₁,A₂) + 0,15p₄(A₁,A₂).

Подставляем разницу в значениях между A₁ и A₂ (табл. 1) в функции приоритетности с последующим их преобразованием в показатели приоритетности (табл. 2):

Q(A₁,A₂) = 0,3p₁(60000 - 42500) + 0,35p₂(800 - 1100) + 0,2p₃ (15 - 12) + 0,15p₄(-35 – (-25));

Q(A₁,A₂) = 0,3p₁(17500) + 0,35p₂(-300) + 0,2p₃ (3) + 0,15p₄(-10);

Q(A₁,A₂) = 0,3 · 1 + 0,35 · 0 + 0,2 · 2/3 + 0,15 · 0 = 0,433.

Так же рассчитывается и значение Q(A₂,A₁)

Q(A₂,A₁) = 0,3p₁(42500 - 60000) + 0,35p₂(1100 - 800) + 0,2p₃ (12 - 15) + 0,15p₄(-25 – (-35));

Q(A₂,A₁) = 0,3p₁(-17500) + 0,35p₂(300) + 0,2p₃ (- 3) + 0,15p₄(10);

Q(A₂,A₁) = 0,3 · 0 + 0,35 · 1 + 0,2 · 0 + 0,15 · 0,1. Q(A₂,A₁) = 0,365.

Расчет значений Quatranking-соотношений, сумм показателей строк F⁺ и столбцов F^¯ приведен в табл. 3.

Таблица 3. Значения Quatranking-соотношений для заданных альтернатив

Альтернативы	А1	А2	А3	А4	А5	F+
А1	0	0,433	0,315	0,300	0,308	1,356
А2	0,365	0	0,330	0,483	0,198	1,375
А3	0,550	0,375	0	0,550	0,550	2,025
А4	0,183	0,067	0,023	0	0,015	0,287
А5	0,242	0,200	0,008	0,308	0	0,758
F¯	1,339	1,075	0,675	1,641	1,070

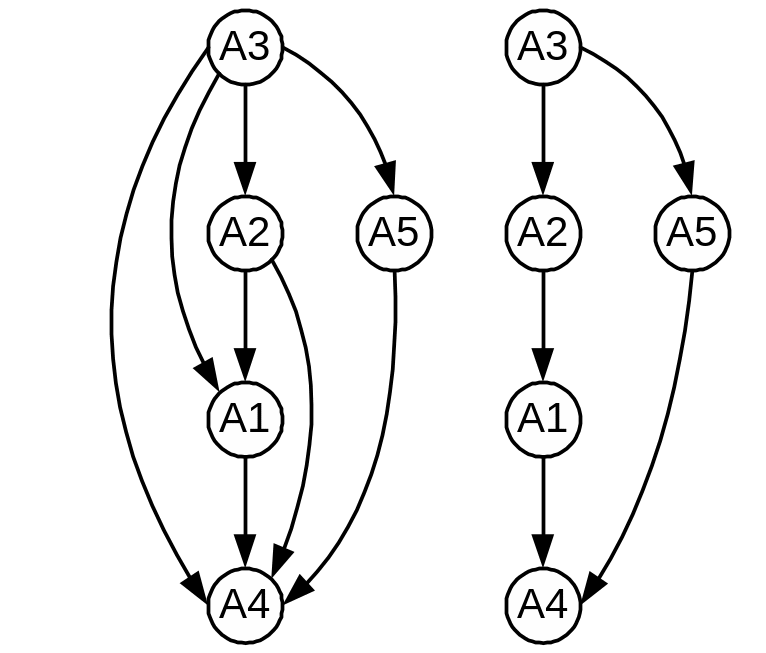
При учете F⁺ и F^¯ составим таблицу частного порядка приоритетности альтернатив (табл. 4). Например, альтернатива А₁ предпочтительнее альтернативы А₄ (это запишем как А₁↑А₄), так как F₁⁺ > F₄⁺ и F₁^¯ < F₄^¯; по сравнению с альтернативой А₂ альтернатива А₁ менее благоприятна (А₂↑А₁), так как F₂⁺ > F₁⁺ и F₂^¯ < F₁^¯; с альтернативой А₅ она не сопоставима (А₁нсА₅), при этом F₁⁺ > F₅⁺ и F₁^¯ > F₅^¯ и т.д.

Если эти отношения изобразить в виде графа, на котором вершины отображают альтернативы, то дуга от вершины А_i к вершине А_k означает предпочтительность альтернативы А_i по отношению к альтернативе А_k, отсутствие дуг между некоторыми вершинами – несопоставимость этих альтернатив; вершина-исток графа – самая приоритетная альтернатива, а вершина-сток - самая слабая из всех альтернатив (рис. 2).

Таблица 4. Частный порядок приоритетности альтернатив (* - сравнение не проводится, «-» - повтор)

Альтернативы	А1	А2	А3	А4	А5
А1	*	А1 А2	А1 А3	А1 А4	А1нсА5
А2	А2 А1	*	А2 А3	А2 А4	А2нсА5
А3	А3 А1	А3 А2	*	А3 А4	А3 А5
А4	А4 А1	А4 А2	А4 А3	*	А4 А5
А5	А5нсА1	А5нсА2	А5 А3	А5 А4	*