3. Розвинення голоморфних функцій в ряд Тейлора.

Теорема 1 (Тейлора). Якщо функція є голоморфною в крузі , то вона єдиним чином розвивається в збіжний в цьому крузі степеневий ряд .

Доведення. Нехай – довільне число. Тоді існує таке, що і . На підставі інтегральної формули Коші

. (1)

Але

,

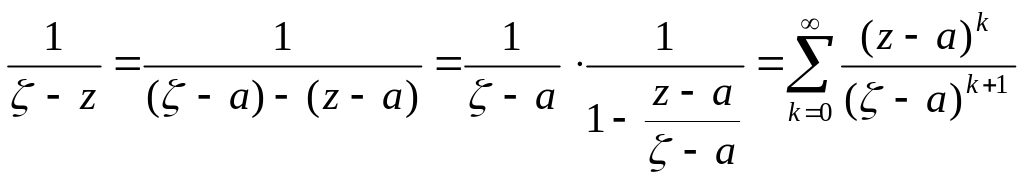якщо , то . Тому на останній ряд збігається рівномірно. Отож, з (1) отримуємо

,

звідки випливає потрібне. ►

Теорема 2. Наступні умови є еквівалентними: 1) функція є голоморфною в точці ; 2) функція має похідну в деякому околі точки ; 3) функція має в точці неперервну похідну; 4) функція має в точці похідну будь-якого порядку ; 5) функція розвивається в деякому околі точки в ряд Тейлора; 6) існує послідовність поліномів, яка рівномірно збігається до в деякому околі точки ; 7) функції і є -диференційовними в деякому околі точки і в цьому околі виконуються умови Коші-Рімана

Доведення. Ця теорема випливає з теорем 1, 2.1, 3.9.2 та 2.2.1. ►

Теорема 2 показує, що можна дати різні еквівалентні означення функції, голоморфної в точці.

Наслідок 1. Кожна голоморфна в області , функція розвивається в збіжний в цій області ряд

,

де

, .

Останній ряд називається рядом Тейлора функції в околі .

Наслідок 2. Якщо функція є голоморфною в крузі , , , і для всіх , то , .

Наслідок 3. Для того, щоб функція була голоморфною в крузі , необхідно і достатньо, щоб вона розвивалась в збіжний в цьому крузі степеневий ряд

. (2)

Наслідок 4. Для того щоб функція була голоморфною в точці , необхідно і достатньо, щоб вона розвивалась в збіжний в деякому околі точки степеневий ряд (2).

Множина функцій , голоморфних в області , називається базою (базисом) простору , якщо кожну функцію , голоморфну в , можна єдиним чином розвинути в ряд

, ,

рівномірно збіжний на кожному компакті з .

Наслідок 5. При будь-якому і будь-якому множина є базою простору . Множина є базою простору для будь-якого .

Наслідок 6. Справедливі розвинення:

а) , ,

б) , ,

в) , ,

г) , ,

д) , ,

е)

,

де – голоморфна гілка в , для якої .

Доведення. Справді, написані функції є голоморфними у вказаних областях. Тому розвиваються в них в ряд Тейлора. Знайшовши коефіцієнти за формулою приходимо до написаних розвинень. ►

Приклад 1. Справедливі рівності

, , , ,

де функції та визначені так само, як і в наслідку 6. Справді, з розвинень б), в), д) та е) маємо, що

, ,

, ,

, ,

, .

Приклад 2. Якщо , то

і останній ряд збігається для всіх .

Приклад 3. Розвинемо в ряд Тейлора в околі точки функцію . Маємо

причому останній ряд збігається в крузі .

Приклад 4. Напишемо перші два члени розвинення в ряд Тейлора в околі точки функції . Маємо , . Тому

Приклад 5. Для кожного функцію

.

Розвинемо в ряд Фур’є на проміжку . Для цього зауважимо, що . Тому, скориставшись розвиненням

,

отримуємо

.

Приклад 6. Покажемо, що розвинення д) з наслідку 6 справедливе на множині . Справді, для кожного ряд

рівномірно збігаться на . Тому

.

З іншого боку, , бо функція є голоморфною, а тому і неперервною в .

Приклад 7. Переконаємось, що функція має похідну в точці тоді і тільки тоді, коли функції та , як функції двох змінних, є диференційовними в цій точці і

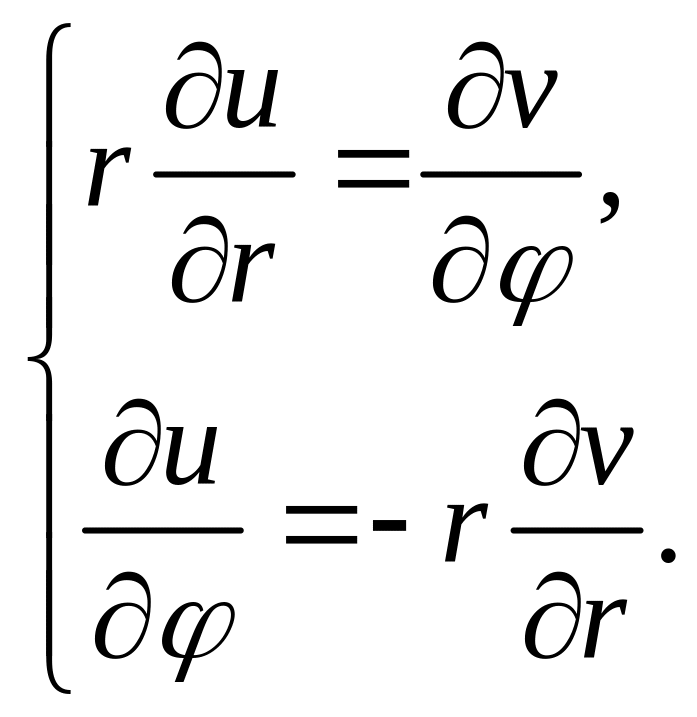
Якщо ці умови виконані, то

Справді, нехай – одиничний вектор нормалі до кола в точці , а – одиничний вектор дотичної до цього кола в цій же точці напрямлений так, що Тоді , ,

,

,

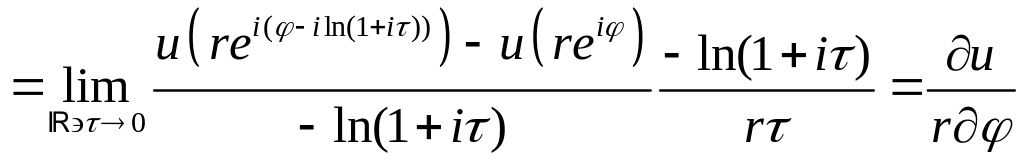де – голоморфна гілка в , для якої . Аналогічно, , . Звідси та з теореми 2.2.1 випливає потрібне.

4. Нулі і множини єдиності. Нулем функції називається таке число , для якого , тобто нуль функції – це число, яке є розв’язком рівняння .

Теорема 1 (єдиності). Якщо множина нулів голоморфної в області функції має граничну точку, яка належить , то , .

Доведення. Нехай – гранична точка множини нулів, а – така послідовність нулів функції , що і . Нехай – відстань від точки до . Тоді в крузі функція є голоморфною і розвивається в ньому в степеневий ряд

,

звідки

.

Звідси, спрямувавши до , отримуємо і тому

.

Перейшовши і в цій рівності до границі отримаємо . Аналогічно показуємо, що і т.д. Отже, всі . Тому , . Нехай тепер – довільна точка області . З’єднаємо точки і ламаною . Оскільки – компакт, то відстань між і є додатною і . Візьмемо на точки , , так, щоб , і довжина частини ламаної, яка лежить між точками була меншою за . Тоді , де і за доведеним вище є граничною точкою нулів функції . В деякому крузі , функція є голоморфною. Тому , якщо , і є граничною точкою нулів функції. Оскільки має скінченну довжину, то за скінченне число кроків ми прийдемо до круга і покажемо, що в цьому крузі. Тому і теорема доведена. ►

Наслідок 1. Якщо функції і є голоморфними в області і для всіх з деякої множини, яка має граничну точку в області , то для всіх .

Ця теорема є іншим формуванням теореми 1.

Наслідок 2. Якщо функція є голоморфною в області , то на кожному компакті з вона має скінченну кількість нулів або зовсім їх не має.

Приклад 1. Теорему єдиності можна застосувати до доведення різних формул. Наприклад, доведемо, що , . Для цього розглянемо функції і . Ці функції є голоморфними в , тобто є цілими, для . Тому на підставі теореми єдиності для всіх і розглядувана формула доведена.

Приклад 2. Покажемо, що не існує голоморфної в крузі функції такої, що

Справді, функція є голоморфною в і . Множина має граничну точку . Тому, якщо , , то , . Але . Отже, такої функції не існує.

Приклад 3. Нехай – голоморфна гілка функції в області , для якої . Тоді для всіх .

Справді, функції та є голоморфними в , для розглядувана формула справедлива, бо для таких символи та означають те ж, що і в дійсному аналізі. Разом з цим, зауважимо, що

, .

Тому . Отже, для формула не обов’язково справедлива. Це пов’язано з тим, що функція не є голоморфною в . Можемо стверджувати також, що існують такі і , що .

Приклад 4. Нехай – голоморфна гілка функції в області , для якої . Тоді для всіх та всіх . Справді, нехай є довільним фіксованим числом. Функції та , як функції змінної , є голоморфними в , і для розглядувана формула справедлива. Робимо висновок, що вона справедлива для всіх та всіх . Нехай тепер є довільним фіксованим числом. Функції та є голоморфними в , як функції змінної , і для кожного розглядувана формула справедлива. Робимо висновок, що вона справедлива для всіх та всіх .

5. Порядок нуля. Нехай функція є голоморфною в області . Нуль функції називається нулем скінченного порядку, якщо існує таке число , що

, . (1)

При цьому це число називається порядком нуля . Нуль називається нулем нескінченного порядку, якщо

. (2)

Нуль порядку називається простим нулем.

Теорема 1. Нехай функція є голоморфною в області . Тоді наступні умови є еквівалентними:

1) в точці функція має нуль порядку ;

2) функція подається у вигляді , де – така голоморфна функція в точці , що ;

3) розвинення функції в ряд Тейлора в околі точки має вигляд

. (3)

Доведення. Справді умови 1) і 3) є еквівалентними, бо . Умови 2) і 3) також є еквівалентними, бо, якщо виконується 3), то

і, позначивши отримуємо 2). З іншого боку, якщо виконується 2) і

,

то

,

звідки випливає 3) і теорема 1 доведена. ►

Теорема 2. Нехай функція є голоморфною в області . Тоді наступні умови є еквівалентними:4) в деякій точці функція має нуль нескінченного порядку; 5) , .

Доведення. Справді, якщо виконується 4), то всі коефіцієнти рівні нулеві. Тому в деякому околі точки і на підставі теореми єдиності , . Навпаки, якщо 5) виконується, то всі похідні функції рівні нулеві. Тому виконується 4). ►

Нехай функція є голоморфною в області і . Точка називається нулем порядку функції , якщо є порядком нуля функції .

Теорема 3. Нехай функція є голоморфною в області і . Тоді наступні умови є еквівалентними:

6) в точці функція має нуль порядку ;

7) подається у вигляді , де – голоморфна і ;

8) розвинення функції в ряд Тейлора в околі має вигляд

.

Доведення. Ця теорема безпосередньо випливає з теореми 1. ►

Нехай – множина нулів функції , голоморфної в області , а – кратність нуля . Множина всіх упорядкованих пар називається дивізором нулів функції , а послідовністю нулів функції називається послідовність побудована так: , . Кількістю нулів функції на множині називається число , тобто .

Приклад 1. Знайдемо порядок нуля функції . Оскільки і то в розглядуваній точці дана функція має простий нуль.

Приклад 2. Знайдемо нулі функції

та їх порядки. Функція має нулі в точках , , і тільки в них. Оскільки і , то в усіх точках функція має прості нулі. Тому подається у вигляді , де – функція, голоморфна в точці і . Функція має нулі в точках та і тільки в них, в точці має нуль порядку , а в точці нуль порядку . Робимо висновок, що , та і функції , та для є голоморфними в точках , та , , відповідно, і їх значення у вказаних точках є відмінними від 0. Тому функція має нуль дев’ятого порядку в точці , нуль третього порядку в точці та прості нулі в точках , .

6. Нерівність Коші. Теорема Ліувілля.

Теорема 1. Нехай функція є голоморфною в крузі , , – її тейлорові коефіцієнти, . Тоді справедливі нерівності Коші:

Доведення. Справді,

Звідси випливає, що

,

що і потрібно було довести. ►

Теорема 2 (Ліувілля). Якщо функція є цілою і обмеженою в , то є сталою.

Доведення. Справді, оскільки обмежена, то . Тому при всіх маємо . Із нерівностей Коші при всіх і отримуємо, що . Спрямувавши до звідси одержуємо, що для всіх . Отже, при всіх , тобто є сталою функцією. ►

Теорема 3 (Ліувілля). Якщо функція є цілою і

,

то – поліном, степінь якого не перевищує .

Доведення цієї теореми аналогічне до доведення теореми 2. ►

Приклад 1 (основна теорема алгебри). Кожний поліном степеня має в принаймні один нуль. Справді, якщо припустити протилежне, то функція буде цілою і обмежено в , а тому є сталою. Отже, – многочлен нульового степеня. Суперечність.