
- •Розділ 4. Розвинення голоморфних функцій в ряди, нулі і особливі точки
- •Приклад 1. Оскільки для , то в півплощині ряд
- •3. Розвинення голоморфних функцій в ряд Тейлора.
- •Розвинемо в ряд Фур’є на проміжку . Для цього зауважимо, що . Тому, скориставшись розвиненням
- •7. Принцип максимуму модуля для голоморфних функцій.
- •14. Запитання для самоконтролю.
- •15. Вправи і задачі.
- •4.31. Обґрунтуйте формули:
Розділ 4
Розділ 4. Розвинення голоморфних функцій в ряди, нулі і особливі точки
1.
Функціональні ряди.
Нехай
![]() – послідовність функцій
– послідовність функцій
![]() .
Ряд
.
Ряд
![]() (1)
(1)
називається
функціональним рядом. Ряд (1) називається
збіжним
на множині
![]() або поточково збіжним на
,
якщо для кожного
або поточково збіжним на
,
якщо для кожного
![]() збіжним є числовий ряд (1), тобто якщо
для кожного
існує
збіжним є числовий ряд (1), тобто якщо
для кожного
існує
![]() ,
,
де
![]()
–
![]() -на
частинна сума ряду (1). Отож, ряд (1)
називається збіжним на множині
,
якщо
-на
частинна сума ряду (1). Отож, ряд (1)
називається збіжним на множині
,
якщо
![]()
Ряд (1) є збіжним на множині тоді і тільки тоді, коли його залишок
![]()
для кожного прямує до нуля, тобто якщо
![]()
Ряд
(1) зветься рівномірно
збіжним
на множині
до
функції
![]() ,
якщо
,
якщо
![]()
Ряд (1) називається рівномірно збіжним на множині , якщо існує функція , до якої він рівномірно збігається на . Іншими словами можна сказати, що ряд (1) називається рівномірно збіжним на множині , якщо його залишок рівномірно прямує до нуля на , тобто якщо
![]()
Теорема 1 (Вейєрштрасса). Якщо існує такий збіжний додатний числовий ряд
![]() ,
,
що
![]() ,
то
на множині
ряд (1) збігається рівномірно
і
абсолютно.
,
то
на множині
ряд (1) збігається рівномірно
і
абсолютно.
Теорема
2.
Якщо
функції
![]() є
неперервними в області
є
неперервними в області
![]() і
ряд (1) рівномірно
збігається
на кожному компакті з
,
то
його сума (функція
)
є неперервною
в
.
і
ряд (1) рівномірно
збігається
на кожному компакті з
,
то
його сума (функція
)
є неперервною
в
.
Теорема
3.
Якщо
функції
є неперервними в області
![]() і ряд (1) є рівномірно збіжним на кожному
компакті з
,
то його можна почленно інтегрувати по
будь-якому спрямлюваному
шляху
і ряд (1) є рівномірно збіжним на кожному
компакті з
,
то його можна почленно інтегрувати по
будь-якому спрямлюваному
шляху
![]() ,
що лежить в
:
,
що лежить в
:
![]() .
.
Доведення теорем 1-3 таке ж, як і відповідних теорем в дійсному аналізі. ►
Теорема
4. Якщо
функції
є голоморфними в області
і ряд (1) є рівномірно збіжний на кожному
компакті з
,
то його сума (функція
![]() )
є голоморфною в
,
)
є голоморфною в
,
![]() ,
(2)
,
(2)
і останній ряд збігається рівномірно на кожному компакті з .
Доведення.
Нехай
![]() – довільна точка області
.
Оскільки
– довільна точка області
.
Оскільки
![]() – голоморфні функції, то
– голоморфні функції, то
![]()
для
кожного спрямлюваного шляху
,
який лежить в достатньо малому околі
точки
.
Тому за теоремою Морери
– голоморфна функція в точці
.
Окрім цього, в кожній точці
![]() для досить малого
для досить малого
![]() маємо
маємо
![]() ,
,
звідки
випливає (2). Оскільки з кожного відкритого
покриття компакта можна виділити
скінченне підпокриття, то рівномірну
збіжність ряду (2) досить довести в
кожному крузі
![]() .
Візьмемо довільно точку
.
Візьмемо довільно точку
![]() і
і
![]() таким, щоб
таким, щоб
![]() .
Тоді для всіх
.
Тоді для всіх
![]()
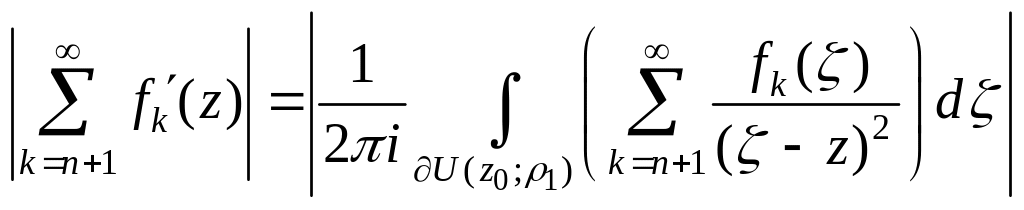
![]() ,
,
бо
![]() ,
де
,
де
![]() ,
,
![]() .
.
Звідси випливає твердження теореми. ►
Наслідок
1.
Якщо
послідовність
голоморфних
в області
функцій
рівномірно збігається на кожному
компакті з
,
то послідовність
![]() також рівномірно збігається на кожному
компакті з
,
функція
також рівномірно збігається на кожному
компакті з
,
функція
![]()
є
голоморфною в
і
![]() .
.
Аналоги попередніх теорем (із такими ж доведеннями) справедливі і для інтегралів.
Теорема
5.
Нехай
![]() для кожного компакту
для кожного компакту
![]() з області
і для майже всіх
з області
і для майже всіх
![]() функція
функція
![]() є голоморфною в
.
Тоді функція
є голоморфною в
.
Тоді функція
![]()
є
голоморфною в
і
![]() .
.
Приклад 1. Оскільки для , то в півплощині ряд
![]()
збігається абсолютно і рівномірно.
Приклад
2. Покажемо,
що ряд
![]() є збіжним в
є збіжним в
![]() і для кожного
і для кожного
![]() на множині
на множині
![]() збігається рівномірно. Справді,
збігається рівномірно. Справді,
![]() ,
,
![]() .
.
Використовуючи рівності
![]() ,
,
![]() ,
,
переконуємось, що частинні суми рядів
![]() ,
,
![]() ,
,
є
обмеженими для кожного
![]() і є рівномірно обмеженими на
і є рівномірно обмеженими на
![]() .
Послідовність
.
Послідовність
![]() рівномірно на
рівномірно на
![]() збігається до
збігається до
![]() .
Тому, використовуючи ознаку Діріхле,
сформульовану для дійсних функціональних
рядів, членами яких є функції
.
Тому, використовуючи ознаку Діріхле,
сформульовану для дійсних функціональних
рядів, членами яких є функції
![]() ,
які подаються у вигляді
,
які подаються у вигляді
![]() приходимо до потрібного висновку.
приходимо до потрібного висновку.
2.
Степеневі ряди.
Степеневий ряд в околі точки
![]() – це функціональний ряд
– це функціональний ряд
![]() ,
(1)
,
(1)
де
![]() і
і
![]() .
Числа
.
Числа
![]() називаються коефіцієнтами степеневого
ряду. Якщо
називаються коефіцієнтами степеневого
ряду. Якщо
![]() ,
то степеневий ряд (1) має вигляд
,
то степеневий ряд (1) має вигляд
![]() .
(2)
.
(2)
Теорема
1 (Абеля).
Якщо
степеневий ряд (1) збігається в точці
![]() ,
то він обсолютно і рівномірно збігається
на кожному компакті із круга
,
то він обсолютно і рівномірно збігається
на кожному компакті із круга
![]() ,
,
![]() .
Якщо степеневий ряд (1) розбігається в
точці
.
Якщо степеневий ряд (1) розбігається в
точці
![]() ,
то він розбігається і зовні круга
,
то він розбігається і зовні круга
![]() ,
.
,
.
Доведення цієї теореми таке ж як і доведення аналогічної теореми в дійсному аналізі.
Радіусом
степеневого ряду називається таке число
![]() ,
що ряд (1) є збіжним, якщо
,
що ряд (1) є збіжним, якщо
![]() ,
і ряд (1) є розбіжним, якщо
,
і ряд (1) є розбіжним, якщо
![]() .
При цьому круг
.
При цьому круг
![]() зветься кругом збіжності. Радіус
збіжності дорівнює точній верхній межі
тих
зветься кругом збіжності. Радіус
збіжності дорівнює точній верхній межі
тих
![]() ,
для яких в крузі
ряд (1) є збіжним. Якщо
,
для яких в крузі
ряд (1) є збіжним. Якщо
![]() ,
то ряд (1) є збіжним тільки в точці
,
то ряд (1) є збіжним тільки в точці
![]() ,
якщо
,
якщо
![]() ,
то ряд (1) є збіжним абсолютно і рівномірно
на кожному компакті з
,
то ряд (1) є збіжним абсолютно і рівномірно
на кожному компакті з
![]() .
Якщо
.
Якщо
![]() ,
то ряд (1) є абсолютно і рівномірно збіжним
на кожному компакті з круга
,
то ряд (1) є абсолютно і рівномірно збіжним
на кожному компакті з круга
![]() і є розбіжним поза кругом
і є розбіжним поза кругом
![]() .
.
Теорема
2.
Радіус
збіжності степеневого ряду (1) знаходиться
за формулою
![]() .
.
Доведення цієї теореми таке ж як і відповідної теореми в дійсному аналізі.
Наслідок
1.
Радіус
збіжності степеневого ряду (1) можна
знайти за формулою
![]() якщо
остання границя існує.
якщо
остання границя існує.
Наслідок
2.
Радіус
збіжності степеневого ряду (1) можна
знайти
за
формулою
![]() ,
якщо
остання границя існує.
,
якщо
остання границя існує.
Теорема
3.
Якщо
степеневий ряд (1) має радіус збіжності
![]() ,
то його сума (функція
)
є голоморфною в крузі
,
то його сума (функція
)
є голоморфною в крузі
![]() ,
ряд (1) можна почленно диференціювати і
ряд
,
ряд (1) можна почленно диференціювати і
ряд
![]() (3)
(3)
також
має радіус збіжності
![]() .
При цьому коефіцієнти
.
При цьому коефіцієнти
![]() ряду (1) можна знайти за кожною з формул
ряду (1) можна знайти за кожною з формул
![]() ,
(4)
,
(4)
![]() ,
,
![]() .
(5)
.
(5)
Доведення.
Справді, функції
![]() є голоморфними в
.
Оскільки на кожному компакті з
ряд (1) збіжний рівномірно, то на підставі
теореми 4 попереднього пункту сума ряду
(1) є голоморфною функцією в
і ряд (1) можна почленно диференціювати.
До того ж,
є голоморфними в
.
Оскільки на кожному компакті з
ряд (1) збіжний рівномірно, то на підставі
теореми 4 попереднього пункту сума ряду
(1) є голоморфною функцією в
і ряд (1) можна почленно диференціювати.
До того ж,
![]() .
.
Тому
радіус збіжності ряду (3) також дорівнює
.
Формулу (4) можна отримати, як і в дійсному
аналізі, почленним диференціюванням
ряду (1), а можна вчинити і так. Помножимо
обидві частини рівності (2) на
![]() .
Тоді, враховуючи, що
.
Тоді, враховуючи, що
![]()
отримаємо
![]() ,
,
звідси випливає (5), а (4) одержують з (5) та формул для знаходження -ої похідної. Теорема 3 доведена. ►
Степеневий
ряд
![]() ,
коефіцієнти
,
коефіцієнти
![]() якого визначені за однією з формул (4),
(5),
називається рядом Тейлора функції
в околі точки
(в крузі
або по степенях
якого визначені за однією з формул (4),
(5),
називається рядом Тейлора функції
в околі точки
(в крузі
або по степенях![]() ).
З теореми 3 випливає, що кожний степеневий
ряд, який має радіус збіжності
).
З теореми 3 випливає, що кожний степеневий
ряд, який має радіус збіжності
![]() є рядом Тейлора своєї суми.
є рядом Тейлора своєї суми.
Приклад 1. Знайдемо радіус і круг збіжності степеневого ряду
![]() .
.
Нехай
![]() .
Тоді
.
Тоді
![]() і
і
![]() .
.
Бачимо,
що розглядуваний ряд буде збіжним, якщо
![]() ,
і буде розбіжним, якщо
,
і буде розбіжним, якщо
![]() .
Робимо висновок, що
.
Робимо висновок, що
![]() – радіус збіжності і
– радіус збіжності і
![]() – круг збіжності. До такого ж висновку
можна прийти наступними міркуваннями.
Оскільки для розглядуваного ряду
– круг збіжності. До такого ж висновку
можна прийти наступними міркуваннями.
Оскільки для розглядуваного ряду
![]()
то
![]()
і на підставі теореми 2 знову приходимо до вказаного вище висновку.
Приклад
2. Якщо
степеневий ряд (1) має радіус збіжності
![]() ,
то для кожного
,
то для кожного
![]() виконується
виконується
![]() ,
,
![]() ,
,
![]() ,
.
,
.
Справді,
![]() ,
а останній ряд також є степеневим і
,
а останній ряд також є степеневим і
![]() – його радіус збіжності. Тому його сума
є обмеженою функцією в деякому околі
точки
– його радіус збіжності. Тому його сума
є обмеженою функцією в деякому околі
точки
![]() .
.
