
- •13 Числовые характеристики непрерывных случайных величин
- •14 Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
- •Функция и ряд распределения
- •Числовые характеристики положения о распределении Пуассона
- •Числовые характеристики разброса
- •Асимметрия и эксцесс распределения Пуассона
14 Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
|
|
Определение
Определение
1. Пусть
задано вероятностное
пространство ![]() ,
и на нём определена случайная величина
,
и на нём определена случайная величина ![]() .
В частности, по определению,
.
В частности, по определению, ![]() является измеримым
отображением измеримого
пространства
является измеримым
отображением измеримого
пространства ![]() в
измеримое пространство
в
измеримое пространство ![]() ,
где
,
где ![]() обозначает борелевскую
сигма-алгебру на
обозначает борелевскую
сигма-алгебру на ![]() .
Тогда случайная величина
индуцирует вероятностную
меру
.
Тогда случайная величина
индуцирует вероятностную
меру ![]() на
следующим
образом:
на
следующим
образом:
![]()
Мера
называется распределением случайной
величины
.
Иными словами, ![]() ,
таким образом
,
таким образом ![]() задаёт
вероятность того, что случайная
величина
попадает
во множество
задаёт
вероятность того, что случайная
величина
попадает
во множество ![]() .
.
[править]Способы задания распределений
Определение
2. Функция ![]() называется (кумулятивной)
функцией распределения случайной
величины
.
Из свойств вероятности вытекает
называется (кумулятивной)
функцией распределения случайной
величины
.
Из свойств вероятности вытекает
Теорема
1. Функция
распределения ![]() любой
случайной величины удовлетворяет
следующим трем свойствам:
любой
случайной величины удовлетворяет
следующим трем свойствам:
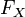 —
функция
неубывающая;
—
функция
неубывающая;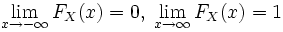 ;
;непрерывна слева.
Из
того факта, что борелевская
сигма-алгебра на
вещественной прямой порождается
семейством интервалов вида ![]() ,
вытекает
,
вытекает
Теорема
2. Любая
функция ![]() ,
удовлетворяющая трём свойствам,
перечисленным выше, является функцией
распределения для какого-то распределения
.
,
удовлетворяющая трём свойствам,
перечисленным выше, является функцией
распределения для какого-то распределения
.
Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания.
[править]Дискретные распределения
Определение
3. Случайная
величина называется простой или дискретной,
если она принимает не более, чем счётное число
значений. То есть ![]() ,
где
,
где ![]() —
разбиение
—
разбиение ![]() .
.
Распределение
простой случайной величины тогда по
определению задаётся: ![]() .
Введя обозначение
.
Введя обозначение ![]() ,
можно задать функцию
,
можно задать функцию ![]() .
Очевидно, что
.
Очевидно, что ![]() .
Используя счётную аддитивность
.
Используя счётную аддитивность ![]() ,
легко показать, что эта функция однозначно
определяет распределение
.
,
легко показать, что эта функция однозначно
определяет распределение
.
Определение 4. Функция , где часто называется дискретным распределением.
Пример
1. Пусть
функция ![]() задана
таким образом, что
задана
таким образом, что ![]() и
и ![]() .
Эта функция задаёт распределение
случайной величины
такой,
что
.
Эта функция задаёт распределение
случайной величины
такой,
что ![]() (распределение
Бернулли).
(распределение
Бернулли).
Теорема 3. Дискретное распределение обладает следующими свойствами:
1. ![]() ;
;
2. ![]() .
.
[править]Непрерывные распределения
Непрерывное распределение — распределение вероятностей, не имеющее атомов. Любое распределение вероятностей есть дискретное, непрерывное или смесь дискретного и непрерывного. В приложениях нередко не делают разницы между терминами непрерывное распределение и абсолютно непрерывное распределение (см. далее).
[править]Абсолютно непрерывные распределения
Основная статья: Плотность вероятности
Абсолютно непрерывными называют распределения, имеющие плотность вероятности. Кумулятивная функция таких распределений абсолютно непрерывна в смысле Лебега.
Определение
5. Распределение
случайной величины
называется
абсолютно непрерывным, если существует
неотрицательная функция ![]() ,
такая что
,
такая что 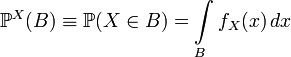 .
Функция
.
Функция ![]() тогда
называется плотностью распределения
случайной величины
.
тогда
называется плотностью распределения
случайной величины
.
Пример
2. Пусть ![]() ,
когда
,
когда ![]() ,
и
,
и ![]() —
в противном случае. Тогда
—
в противном случае. Тогда  ,
если
,
если ![]() .
.
Очевидно,
что для любой плотности распределения
верно
равенство 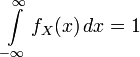 .
Верна и обратная
.
Верна и обратная
Теорема
4. Если
функция ![]() такая,
что:
такая,
что:
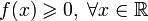 ;
;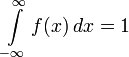 ,
,
то
существует распределение
такое,
что ![]() является
его плотностью.
является
его плотностью.
Просто применение формулы Ньютона-Лейбница приводит к простому соотношению между кумулятивной функцией и плотностью абсолютно непрерывного распределения.
Теорема 5. Если — непрерывная плотность распределения, а — его кумулятивная функция, то

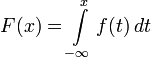 .
.
15. Распределение Пуассона в теории вероятностей
