3.3. Решение системы дифференциальных уравнений с помощью электронных таблиц Excel

Решим задачу при , , , , , .

В ячейки A2 запишем начальное значение времени – 0. В ячейку A3 запишем формулу

=A2+$H$2,

определяющую значение следующего момента времени (шаг по времени помещен в ячейке H2 – см. рис. 3.1). Распространим формулу по ячейку A1202. Значение ячейке A1202 должно быть равно 12.

В ячейки B2 и C2 запишем начальные значения (рис. 3.1), в ячейку B3 запишем формулу, соответствующую первому уравнению системы

=B2+$H$2*($D$2*B2-$F$2*B2*C2),

а в ячейку C3 запишем формулу, соответствующую второму уравнению системы

=C2+$H$2*(-$E$2*C2+$G$2*B2*C2)

Распространим формулы по ячейки B1202 и C1202.

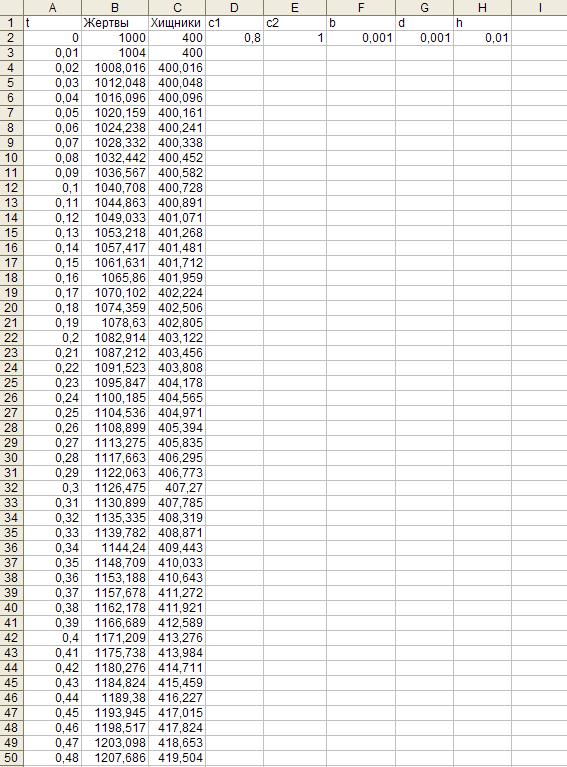
Рис. 3.1. Фрагмент заполненной таблицы

Построим график зависимости численности жертв и хищников от времени. Выделим ячейки A2:C1202,вызовем Мастер диаграмм (кнопка на инструментальной панели Excel). В первом шаге Мастера (рис. 3.2) выбираем тип диаграммы: стандартная, точечная и вид диаграммы: "Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров".

Рис. 3.2. Выбор вида диаграммы

Построим график зависимости численности хищников от численности жертв. График построим как точечную диаграмму для первого периода изменения численности жертв (из графика видно, что первому периоду соответствует интервал времени от 0 до 7,2). Вид в Мастере диаграмм: "Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров". Таблица с графиками представлена на рис. 3.3.

Рис. 3.4. Таблица с графиками

Численности популяций жертв и хищников совершают периодические колебания вокруг положения равновесия , . Колебания совершаются не в фазе: максимальному значению численности жертв соответствует стационарное значение численности хищников и наоборот. Это объясняется тем, что рост численности хищников приводит к уменьшению численности жертв. Вызванный этим дефицит пищи приводит к сокращению численности хищников, что способствует увеличению поголовья жертв и т. д. На фазовой плоскости зависимость численности хищников от численности жертв имеет вид, близкий к эллипсу с центром в точке ( ).

3.4. Контрольные вопросы

1. Объясните характер поведения графиков рис. 3.3.

2. Каким недостатком обладает модель Лотки‑Вольтерры, продемонстрируйте проявление этого недостатка.

3. Какие социальные явления описываются уравнениями, аналогичными ?

3.5. Задания

1. Исследуйте влияние на характер решения следующих факторов:

– начальная численность популяций;

– скорости прироста численности жертв и убыли хищников.

2. Постройте решение и графики при различных значениях.

4. ИССЛЕДОВАНИЕ МОДЕЛЕЙ ДИНАМИЧЕСКОГО ХАОСА

4.1. Цель работы

Исследование моделей динамического хаоса.

4.2. Постановка задачи

Рассмотрим логистическое разностное уравнение [5], описывающее распространение инноваций на рынке

.

В емкость рынка равна 1, , т. е. – доля рынка, завоеванная инновацией к моменту времени , – параметр скорости роста инноваций.

4.3. Исследование динамического хаоса с помощью электронных таблиц Excel

Исследуем решение уравнения с помощью электронных таблиц Excel. Примем, что время изменяется от 1 до 60 с шагом 1. Поэтому столбец времени в таблице отсутствует. В ячейке A2 запишем начальное значение (рис. 4.1). В ячейке C2 хранится значение параметра (на рис. 4.1 ). В ячейке A3 записана формула

=$C$2*A2*(1-A2).

Столбец B является вспомогательным, равным столбцу A со сдвигом на одну ячейку вниз (столбец B потребуется для построения графиков). Для этого в ячейке B3 записана формула =A2.

Рис. 4.1. Фрагмент таблицы

Выделим ячейки A3 и B3 и размножим в этих ячейках по строку 61.

Построим два вида графиков:

– график зависимости решения от времени ;

– график, описывающий поведение системы в фазовой плоскости .

Для построения графика выделим ячейки A2–A61 и построим стандартный график, отображающий развитие процесса по времени или по категориям.

Для построения второго графика выделим ячейки A2–B61 и построим точечную диаграмму со значениями, соединенными сглаживающими линиями. При построении графика обратите внимание на правильность выбора значений по осям X и Y(рис. 4.2).

Рис. 4.2. Построение зависимости на фазовой плоскости

Примеры графиков для приведены на рис. 4.3.

Рис. 4.3. Примеры графиков

Поведение решения уравнения зависит от значения параметра , которое может изменяться от 0 до 4 ( ). Зависимость типа поведения решения от параметра показана в табл. 4.1.

Таблица 4.1. Зависимость типа поведения решения от значения параметра

Тип поведения	Значение параметра	Примечания
Состояние равновесия		При решение стремится к состоянию равновесия . При решение стремится к .
Периодические колебания	точка бифуркации	– колебания с периодом 2 – колебания с периодом 4 – колебания с периодом 8 – колебания с периодом 16
Хаотический режим	точка бифуркации

Если , то решение стремится к стационарному состоянию , то есть аттрактором является точка , что видно на фазовой плоскости (рис. 4.3).

При решение стремится к (рис. 4.4).

Рис. 4.4. Пример поведения решения при c=2,600

При c=3,200 система переходит к колебаниям с периодом, равным 2 (рис. 4.5). Аттрактором является цикл, состоящий из 2 точек.

Рис. 4.5. Пример поведения решения при c=3,200

При c=3,900 поведение системы носит хаотический характер (рис. 4.6).

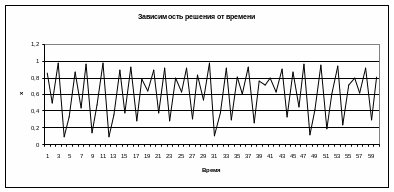
Рис. 4.6. Пример поведения решения при c=3,900

На рис. 4.6 мы видим странный аттрактор, в котором не видно никаких закономерностей. Но если тип графика в фазовой плоскости изменить на точечный (рис. 4.7), то видно, что состояния системы изменяются по вполне не случайной форме, близкой к параболе.

Рис. 4.7. Портрет странного аттрактора