- •Раздел 1 основные понятия навигации
- •Глава 1
- •Ориентирование на морской поверхности земли
- •§ 1. Форма земли и ее модели
- •§ 2. Основные точки и линии на земном эллипсоиде и на земном шаре
- •§ 3. Основные линии и плоскости наблюдателя для ориентирования в море
- •§ 4. Координаты точки на поверхности земли и ее моделях
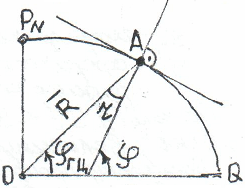
- •5.1Плоский угол между плоскостью гринвичского меридиана и линией dc, которая является проекцией вертикали точки а на плоскость земного экватора.
- •5.2Двугранный угол между плоскостью гринвичского меридиана и плоскостью астрономического меридиана точки а.
- •5.3Сферический угол fca между гринвичским меридианом и астрономическим меридианом точки а.
- •§ 5. Измерение географических координат на морской навигационной карте
- •§ 6. Разность широт и разность долгот двух точек
- •§ 7. Вычисление разности широт и разности долгот двух точек
- •§ 8. Кривизна земного эллипсоида
§ 4. Координаты точки на поверхности земли и ее моделях
Координаты точки (от лат. со – совместно и ordinates – упорядоченный, определенный) – это линейные и (или) угловые величины, которые определяют положение точки на плоскости, на поверхности объемной фигуры и в пространстве.
Д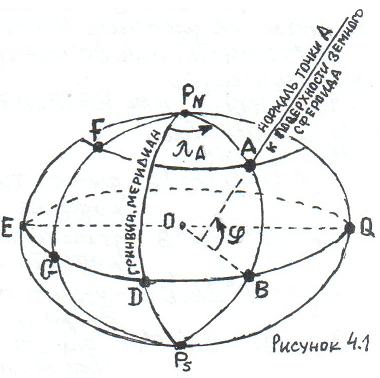 ля
определения положения точки на поверхности
Земли и ее моделях применяют следующие
координатные системы:
ля
определения положения точки на поверхности
Земли и ее моделях применяют следующие
координатные системы:
1. Географические координаты точки.
2. Сферические координаты точки.
3. Геоцентрические координаты точки.
4. Геодезические координаты точки.
5. Астрономические координаты точки.
6. Полярные координаты точки.
Географические координаты точки – это угловые величины – географическая широта и географическая долгота, которые определяют положение точки на поверхности земного сфероида относительно земного экватора и гринвичского меридиана.
Географическая широта точки А (рисунок 4.1) – это плоский угол φ (фи) между плоскостью земного экватора и нормалью этой точки к поверхности земного сфероида.
Географическую широту точки А измеряют
с помощью дуги меридиана точки А (![]() ),
которая заключена между земным экватором
и этой точкой (рисунок 4.1). Если провести
параллель точки А, то дуги всех меридианов,
заключенные между земным экватором и
параллелью этой точки, будут равны по
длине (
),
которая заключена между земным экватором
и этой точкой (рисунок 4.1). Если провести
параллель точки А, то дуги всех меридианов,
заключенные между земным экватором и
параллелью этой точки, будут равны по
длине (![]() ).
Поэтому географическую широту точки
можно измерить или вычислить с помощью
дуги любого меридиана, которая заключена
между земным экватором и параллелью
этой точки. Географическую широту точки
измеряют или вычисляют в следующих
угловых единицах:
).
Поэтому географическую широту точки
можно измерить или вычислить с помощью
дуги любого меридиана, которая заключена
между земным экватором и параллелью
этой точки. Географическую широту точки
измеряют или вычисляют в следующих
угловых единицах:
- в радианах;
- в градусах, минутах и секундах;
- в градусах, минутах и десятых долях минуты;
- в градусах, минутах и сотых долях минуты;
- в градусах, минутах и тысячных долях минуты.
Географическую широту точки измеряют в диапазоне 0º-90º в следующих направлениях:
- от нуля градусов на земном экваторе до девяноста градусов в сторону северного истинного полюса Земли (РN);
- от нуля градусов на земном экваторе до девяноста градусов в сторону южного истинного полюса Земли (РS).
Таким образом, точка А в северном полушарии и точка С в южном полушарии могут иметь равные числовые значения географической широты.
Для исключения неоднозначности - географической широте точки присваивают следующие наименования:
- северная (С) или нордовая (N) широта точки, если эта точка находится в северном полушарии;
- южная (Ю) или зюйдовая (S) широта точки, если эта точка находится в южном полушарии.
Например:
-
![]() – широта точки А пятьдесят три градуса,
четырнадцать минут и тридцать шесть
секунд северная;
– широта точки А пятьдесят три градуса,
четырнадцать минут и тридцать шесть
секунд северная;
-
![]() – широта точки С пятьдесят три градуса,
четырнадцать минут и тридцать шесть
секунд южная;
– широта точки С пятьдесят три градуса,
четырнадцать минут и тридцать шесть
секунд южная;
-
![]() – широта точки пять градусов, пять и
семь десятых минуты нордовая;
– широта точки пять градусов, пять и
семь десятых минуты нордовая;
-
![]() – широта точки двадцать четыре градуса,
восемь и три десятых минуты зюйдовая;
– широта точки двадцать четыре градуса,
восемь и три десятых минуты зюйдовая;
-
![]() –
широта точки сорок четыре градуса, одна
и четыре сотых минуты нордовая;
–
широта точки сорок четыре градуса, одна
и четыре сотых минуты нордовая;
-
![]() – широта точки три градуса, семь и восемь
тысячных минуты зюйдовая.
– широта точки три градуса, семь и восемь
тысячных минуты зюйдовая.
Г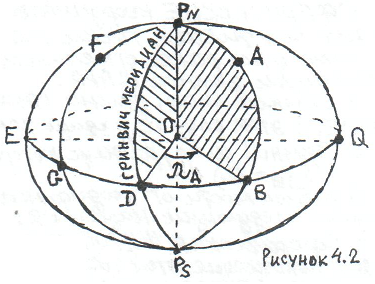 еографическая
долгота точки А (рисунок 4.2) – это
двугранный угол λ (лямбда) между плоскостью
гринвичского меридиана и плоскостью
меридиана этой точки А.
еографическая
долгота точки А (рисунок 4.2) – это
двугранный угол λ (лямбда) между плоскостью
гринвичского меридиана и плоскостью
меридиана этой точки А.
Плоскость гринвичского меридиана – это плоскость сечения земного сфероида DPNOPS (рисунок 4.2), которая проходит через гринвичский меридиан и ось вращения Земли.
Плоскость меридиана точки А – это плоскость сечения земного сфероида APNOPSB, которая проходит через меридиан точки А и ось вращения Земли.
Географическую долготу точки А можно измерить или вычислить в таких угловых единицах, как радианы, угловые градусы, минуты и секунды или градусы, минуты и десятые (сотые, тысячные) доли минуты двумя способами:
1. С помощью дуги земного экватора
(![]() рисунок
4.2), которая заключена между гринвичским
меридианом и меридианом точки А.
рисунок
4.2), которая заключена между гринвичским
меридианом и меридианом точки А.
2. С помощью сферического угла DPNAB при северном истинном полюсе Земли PN между гринвичским меридианом и меридианом точки А.
Географическую долготу точки измеряют в диапазоне 0º-180º в следующих направлениях:
- от нуля градусов на гринвичском меридиане до ста восьмидесяти градусов в сторону востока;
- от нуля градусов на гринвичском меридиане до ста восьмидесяти градусов в сторону запада.
Таким образом, точка А в восточном полушарии и точка F в западном полушарии могут иметь равные числовые значения географической долготы. Для исключения неоднозначности – географической долготе точки, присваивают следующие наименования:
- Восточная (В) или остовая (Е) долгота точки – если эта точка находится в восточном полушарии;
- Западная (З) или вестовая (W) долгота точки – если эта точка находится в западном полушарии.
Например:
-
![]() -
долгота точки А – тридцать шесть
градусов, сорок минут и тринадцать
секунд восточная;
-
долгота точки А – тридцать шесть
градусов, сорок минут и тринадцать
секунд восточная;
-
![]() -
долгота точки F – тридцать
шесть градусов, сорок минут и тринадцать
секунд западная;
-
долгота точки F – тридцать
шесть градусов, сорок минут и тринадцать
секунд западная;
-
![]() -
долгота точки і – сто
семьдесят шесть градусов, двадцать
четыре и шесть десятых минуты остовая.
-
долгота точки і – сто
семьдесят шесть градусов, двадцать
четыре и шесть десятых минуты остовая.
-
![]() -
долгота точки і – девяносто
семь градусов, две и пять тысячных
минуты вестовая.
-
долгота точки і – девяносто
семь градусов, две и пять тысячных
минуты вестовая.
Сферические координаты точки – это угловые величины – сферическая широта и сферическая долгота точки, которые определяют положение данной точки на поверхности земного шара относительно земного экватора и гринвичского меридиана.
|
Рисунок 4.3 |
Радиус земного шара в точке А – это радиус шара, проходящий через эту точку.
Сферическую широту точки А измеряют дугой любого меридиана, которая заключена между земным экватором и параллелью этой точки от нуля градусов на земном экваторе до девяноста градусов в сторону северного истинного полюса и в сторону южного истинного полюса.
Сферическая долгота точки А (рисунок 4.3) – это двугранный угол между плоскостью гринвичского меридиана и плоскостью меридиана точки.
Плоскость гринвичского меридиана – это плоскость сечения земного шара, проходящая через гринвичский меридиан и ось вращения Земли.
Плоскость меридиана точки А – это плоскость сечения земного шара, проходящая через меридиан точки А и ось вращения Земли.
Сферическую долготу точки А можно измерить или вычислить двумя способами:
1. С помощью дуги земного экватора ( рисунок 4.3), которая заключена между гринвичским меридианом и меридианом этой точки от нуля градусов на гринвичском меридиане до ста восьмидесяти градусов в сторону востока и в сторону запада.
2. С помощью сферического угла DPNB при северном истинном полюсе Земли PN между гринвичским меридианом и меридианом точки А.
|
Рисунок 4.4 |
Геоцентрическая широта точки А
(рисунок 4.4) – это плоский угол φгц
между плоскостью земного экватора и
радиусом-вектором земного эллипсоида
в этой точке. Радиус-вектор (![]() )
эллипсоида в какой-либо точке – это
отрезок прямой, соединяющий центр
эллипсоида с этой точкой. Разность между
географической и геоцентрической
широтами (
)
эллипсоида в какой-либо точке – это
отрезок прямой, соединяющий центр
эллипсоида с этой точкой. Разность между
географической и геоцентрической
широтами (![]() )
называется редукцией широты, величину
которой можно вычислить по формуле:
)
называется редукцией широты, величину
которой можно вычислить по формуле:
![]() ,
(4.1)
,
(4.1)
где
![]() -
редукция широты, секунды;
-
редукция широты, секунды;
- степень полярного сжатия земного эллипсоида;
![]() - географическая широта произвольной
точки і;
- географическая широта произвольной
точки і;
![]() - величина одной угловой
секунды (
- величина одной угловой
секунды (![]() ),
выраженная в радианах:
),
выраженная в радианах:
![]()
Согласно формуле (4.1) редукция широты
достигает максимального значения на
широте 45º (![]() ).
Так, например, если точка і
находится на эллипсоиде Красовского,
то
).
Так, например, если точка і
находится на эллипсоиде Красовского,
то
![]() .
Тогда:
.
Тогда:
![]()
Геоцентрическая долгота точки (λгц) равна географической долготе этой точки (λгц = λ), т.к. радиус-вектор земного эллипсоида в какой-либо точке находится в плоскости меридиана этой точки.
Геоцентрические координаты
применяются для решения некоторых
математических задач астрономии
(от греч. astron – звезда и
nomos – закон), картографии
(от греч. chartёs
– лист или свиток папируса и
![]() - пишу) и гироскопии (от греч.
- пишу) и гироскопии (от греч.
![]() –
кружусь, вращаюсь и
–
кружусь, вращаюсь и
![]() – смотрю – наука о быстровращающемся
теле).
– смотрю – наука о быстровращающемся
теле).
Геодезические координаты точки – это угловые величины – геодезическая широта и геодезическая долгота точки, а также линейная величина – геодезическая высота точки, которые определяют положение этой точки на поверхности планеты Земля относительно поверхности земного сфероида.
|
Рисунок 4.5 |
1. Фигуру планеты Земля совмещают с земным сфероидом так, чтобы малая ось земного сфероида совпала с осью вращения Земли, а плоскость земного экватора этого сфероида совпала с земным экватором планеты Земля.
2. Через точку А земной поверхности проводят нормаль к поверхности земного сфероида (АВ).
3. Измеряют географические координаты точки С, которая является проекцией точки А планеты Земля на поверхность земного сфероида:
3.1 Географическую широту точки С
(![]() ).
).
3.2 Географическую долготу точки С
(![]() ).
).
4. С помощью отрезка АС измеряют геодезическую высоту точки А относительно поверхности земного сфероида.
Астрономические координаты точки – это угловые величины – астрономическая широта точки и астрономическая долгота точки, которые определяют положение этой точки на поверхности геоида и на небесной сфере.
Для измерения астрономических координат точки А на поверхности геоида производят следующие геометрические построения (рисунок 4.6):
1. Проводят вертикаль точки А до пересечения с плоскостью земного экватора в точке В. Поскольку вертикаль точки обычно отклонена от плоскости географического (истинного) меридиана, то точка В расположена на некотором удалении от линии ОЕ, которая является линией пересечения плоскости истинного меридиана точки А с плоскостью земного экватора (линия пересечения плоскости PNAEO с плоскостью OEF).
|
Рисунок 4.6 |
3. Плоский угол АВС между плоскостью
земного экватора и вертикалью точки А
называется астрономической широтой
точки А (![]() ).
).
4. Через вертикаль точки А, через линию ВС и через линию АС проводят плоскость ACDK, которая является вертикальной плоскостью и называется плоскостью астрономического меридиана точки А. Поскольку плоскость ACDK проходит через линию АС, которая является перпендикуляром к плоскости земного экватора и поэтому параллельна оси вращения геоида PN-PS, то плоскость астрономического меридиана точки А в отличии от плоскости истинного меридиана этой точки не проходит через ось вращения геоида, а параллельна этой оси. Кривая АК является линией пересечения плоскости астрономического меридиана с поверхностью геоида и называется астрономическим меридианом точки А.
5. Астрономическую долготу точки А определяют три угла: