
- •3.1. Границя числової послідовності
- •Дійсно, згідно означення границі
- •3.2. Основні положення про границі числових послідовностей
- •3.3. Нескінченні границі
- •3.4. Число е. Натуральні логарифми
- •3.5. Границя функції на нескінченності і в точці
- •Нерівність еквівалентна подвійній нерівності .
- •3.6. Нескінченно малі та нескінченно великі величини
- •3.7. Зв’язок між нескінченно малими і нескінченно великими
- •3.8. Порівняння нескінченно малих та нескінченно великих величин
- •Аналогічні порівняння мають місце і для нескінченно великих величин.
- •3.9. Основні теореми про границі функції
- •3.10. Розкриття деяких невизначеностей
- •Невизначеність вигляду , задана відношенням двох многочленів
- •Невизначеність вигляду , задана ірраціональними виразами
- •Невизначеність вигляду , задана відношенням двох многочленів
- •Невизначеність вигляду , задана ірраціональними виразами
- •3.11. Дві важливі границі Перша важлива границя
- •3.12. Задача про неперервне нарахування відсотків
- •3.13. Неперервність функції
- •3.13.2. Розрив функції. Класифікація точок розриву
- •3 Рис. 7 .13.3. Властивості неперервних функцій
Невизначеність вигляду , задана ірраціональними виразами
Приклад.
Знайти
![]() .
.
Розв’язання.
При
![]() маємо невизначеність
,
отже
маємо невизначеність
,
отже
![]() – критичний множник. Позбудемося
ірраціональності в чисельнику. Маємо
– критичний множник. Позбудемося
ірраціональності в чисельнику. Маємо

![]() .
.
Невизначеність вигляду , задана відношенням двох многочленів
Нехай потрібно знайти границю дробово-раціональної функції
 .
.
Розглянемо такі випадки:
а)
Нехай
![]() ,
тоді, розділивши чисельник і знаменник
на
,
тоді, розділивши чисельник і знаменник
на
![]() ,
знаходимо
,
знаходимо
 .
.
Якщо
тепер перейти до границі у кожному
доданку чисельника і знаменника, то у
чисельнику дістанемо число
![]() ,
а у знаменнику – нескінченність.
Відношення скінченого числа до
нескінченної величини є нескінченно
мала величина, тобто
,
а у знаменнику – нескінченність.
Відношення скінченого числа до
нескінченної величини є нескінченно
мала величина, тобто
![]() .
.
б)
Нехай
![]() ,
тоді, розділивши чисельник і знаменник
на
,
тоді, розділивши чисельник і знаменник
на
![]() ,
дістанемо
,
дістанемо
 .
.
в)
Нехай
![]() ,
тоді, розділивши чисельник і знаменник
на
,
тоді, розділивши чисельник і знаменник
на
![]() ,
знаходимо
,
знаходимо
 .
.
Якщо
тепер перейти до границі у кожному
доданку чисельника і знаменника, то у
чисельнику дістанемо нескінченність,
а у знаменнику – число
![]() .
Таке відношення дає нескінченно велику
величину, тобто
.
Таке відношення дає нескінченно велику
величину, тобто
![]() .
.
Таким чином,
 .
.
Приклад.
Знайти
![]() .
.
Розв’язання.
Маємо
невизначеність
![]() .
Поділимо чисельник і знаменник дробу
на
.
Поділимо чисельник і знаменник дробу
на
![]() .
.
 .
.
Невизначеність вигляду , задана ірраціональними виразами
Приклад.
Знайти
![]() .
.
Розв’язання. Маємо невизначеність . Для розкриття невизначеності потрібно позбутись ірраціональності в чисельнику:

 .
.
3.11. Дві важливі границі Перша важлива границя
![]() .
.
Доведення.
Функція
![]() визначена в області
визначена в області
![]() .
Оскільки має місце рівність
.
Оскільки має місце рівність
![]() ,
то функція парна, з чого випливає, що
вона симетрична відносно осі ординат.
Тому, якщо в точці
існують однобічні границі, то вони рівні
між собою, тобто:
,
то функція парна, з чого випливає, що
вона симетрична відносно осі ординат.
Тому, якщо в точці
існують однобічні границі, то вони рівні
між собою, тобто:
![]()
Розглянемо границю цієї функції в точці справа і доведемо, що .
Рис.
4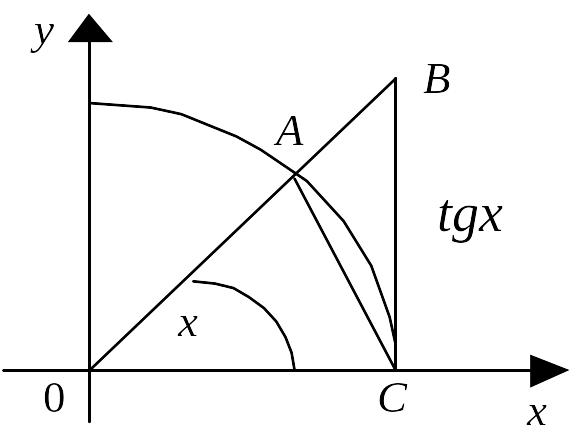
![]() коло одиничного радіуса (рис. 4) і візьмемо
кут х
коло одиничного радіуса (рис. 4) і візьмемо
кут х
![]() ,
який дорівнює аргументу функції.
,
який дорівнює аргументу функції.
Тоді:
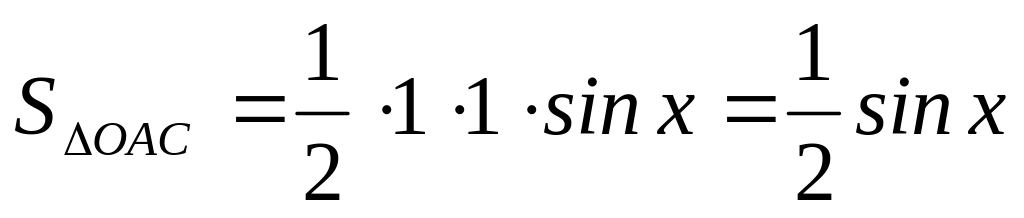 ;
; ;
; .
.
Порівнюючи площі трикутників ОАС, ОВС і колового сектора ОАС, дістанемо
![]() ,
,
звідки
![]() .
.
Розділивши
останні нерівності на
![]() ,
дістанемо
,
дістанемо
![]() або
або
![]() .
.
Оскільки
![]() ,
то згідно теореми “про два міліціонери”,
маємо
.
,
то згідно теореми “про два міліціонери”,
маємо
.
Приклад
1.
Знайти
![]() ,
при
,
при
![]() .
.
Розв’язання.
Зведемо розглядувану границю до першої
важливої границі, помноживши та поділивши
дріб на а
та ввівши позначення
![]() :
:
![]() .
.
Друга важлива границя
![]() ,
,
![]() . (6) Доведення.
Вище було показано, що
,
де
. (6) Доведення.
Вище було показано, що
,
де
![]() – натуральне число.
– натуральне число.
Спочатку доведемо, що має місце рівність
![]() . (7)
. (7)
Нехай
х
дійсне число, ціла частина якого![]() .
Тоді
.
Тоді
![]() або
або
![]() з чого випливає, що
з чого випливає, що
![]() .
.
Враховуючи,
що
![]() ,
дістанемо нерівності
,
дістанемо нерівності
![]() . (8)
. (8)
Знайдемо
границі лівої і правої частини нерівності
(8) при
![]() :
:
![]() ,
,
![]() .
.
Оскільки
з нерівності
при
випливає, що
![]() ,
а у нерівності (8) ліва і права частини
при
прямують до однієї і тієї самої границі,
що дорівнює е,
то за теоремою Гур’єва
,
а у нерівності (8) ліва і права частини
при
прямують до однієї і тієї самої границі,
що дорівнює е,
то за теоремою Гур’єва
.
Покажемо, що
![]() .
(9)
.
(9)
Для
доведення введемо змінну
![]() .
Оскільки при
.
Оскільки при
![]() ,
то
,
то

де
![]() .
.
Об’єднавши випадки (7) і (8), дістанемо границю (6).
Поклавши
![]() і врахувавши, що при
і врахувавши, що при
![]() ,
дістанемо
,
дістанемо
![]() . (10)
. (10)
Одержана границя співпадає з точністю до позначення змінної із другою формулою (6).
Зауваження. При обчисленні границь, пов’язаних з числом, часто користуються таким твердженням:
Якщо
існують границі
![]() ,
,
![]() ,
причому
,
причому
![]() ,
то існує також границя
,
то існує також границя
![]() ,
яка обчислюється за формулою
,
яка обчислюється за формулою
![]() . (11)
. (11)
Приклад
1.
Знайти
![]() .
.
Скориставшись формулою (6), дістанемо
 .
.
Приклад
2. Знайти
![]() .
.
Скориставшись формулами (6) та (11), дістанемо


