6.6. Векторное и смешанное произведение. Площади и объемы

Векторным произведением [a  b] векторов a и b называется вектор c, который равен определителю, в первой строке которого стоят стандартные базисные орты, а во второй и третьей строке координаты векторов-сомножителей

(57)

Векторное произведение обозначается также [ab] или a  b.

Свойства векторного произведения:

1. [a  b] = [b  a] в отличие от скалярного произведения, векторное произведение антикоммутативно.

2. [a  b] = [a  b] = [ab] числовой множитель можно выносить за знак векторного произведения.

3. [a  (b + с)] = [a  b] + [a  с] для векторного произведения справедлив распределительный (дистрибутивный) закон

4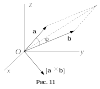 . [a  b] = 0 тогда и только тогда, когда векторы a и b параллельны. В частности, [a  0] = 0 a (т. о., нуль-вектор параллелен любому вектору).

С войства 14 векторного произведения есть очевидные следствия свойств определителей, приведенных в пункте 3.3. Так свойство 1 следует из свойства 4 п. 3.3, свойство 2  из свойства 2 п. 3.3 и т. д.

Можно показать, что модуль векторного произведения не изменяется при переходах от одного ортонормированного базиса к другому. Направление векторного произведения изменится на противоположное, если один из векторов базиса изменит направление на противоположное.

Подобно скалярному, векторному произведению можно дать геометрическое, то есть, не зависящее от выбора системы координат, определение. Векторным произведением [a  b] векторов a и b называется вектор c, который:

1) перпендикулярен плоскости векторов a и b;

2) направлен так, что если смотреть из его конца, то для совмещения сомножителей первый сомножитель ко второму следует поворачивать против часовой стрелки;

3) модуль векторного произведения равен площади параллелограмма, построенного на векторах-сомножителях, т. е. произведению длин векторов-сомножителей на синус угла между ними:

|[a  b]|= |a| |b|sin, (58)

в частности, модуль векторного произведения взаимно перпендикулярных векторов равен произведению длин векторов-сомножителей.

Легко убедиться, что орты стандартного базиса связаны соотношением [i  j] = k. Такие системы координат (базисы), третий орт которых есть векторное произведение первого орта на второй, называются левоориентированными или просто левыми, если же [i  j] =  k, то такие системы координат (базисы) называются правоориентированными или же правыми. При переходах между базисами различной ориентации векторное произведение меняет направление на противоположное (меняет знак).

Векторное произведение естественно использовать в задачах, связанных с вычислением площадей. Как следует из (57) и (58), площадь параллелограмма, построенного на векторах a и b равна:

|[ab]|= . (60)

6.6.1. Смешанное произведение и вычисление объемов

Умножим векторное произведение векторов a и b скалярно на некоторый третий вектор с: (с [a  b])  такое произведение трех векторов называется скалярно-векторным или смешанным произведением

. (61)

Сумма, стоящая в правой части (61), получилась как сумма попарных произведений координат сомножителей, с учетом того, что координаты [a  b] есть коэффициенты при i, j, k в выражении (57). Правая часть (61) есть правая часть (57), в которой векторы i, j, k заменили координатами вектора с: c_x, c_y, c_z. Значит правая часть выражения (61) представляет собой разложение по элементам первой строки определителя

. (62)

Смешанное произведение трех векторов равно определителю, по строкам которого стоят координаты векторов в том порядке, как они записаны в смешанном произведении.

Смешанное произведение наследует общие свойства векторного и скалярного произведения, а именно:

 множитель, стоящий перед любым из сомножителей, можно выносить за знак смешанного произведения;

 смешанное произведение дистрибутивно: «произведение суммы равно сумме произведений», т. е. если один из сомножителей представлен в виде суммы, то смешанное произведение равно сумме соответствующих смешанных произведений, например: (с [a + d  b]) = (с [a  b]) + (с [d  b])

 модуль смешанного произведения трех взаимно ортогональных векторов равен произведению их длин (проверьте!);

 если поменять местами любые два сомножителя, смешанное произведение сменит знак (очевидное следствие свойств определителей).

В ыясним вопрос о геометрическом смысле смешанного произведения. Пусть для наглядности сомножители a и b, входящие в векторное произведение, расположены в плоскости xOу, а вектор c расположен под некоторым углом к плоскости xOу (см. рис.12). Тогда векторное произведение [a  b] параллельно оси z, а величина смешанного произведения равна произведению |[a  b]| на проекцию вектора с на вектор [a  b], т. е. на ось z: |(с[a  b])| = |[a  b]|Пр_zс. Если построить на векторах a,b,c параллелепипед, то Пр_zс будет его высотой, а |[a  b]|  площадью параллелограмма, лежащего в основании. Но произведение площади основания на высоту есть объем параллелепипеда. Таким образом, модуль смешанного произведения равен объему параллелепипеда, построенного на векторах-сомножителях.

Полученный нами результат допускает обобщение. В самом деле, если векторы a и b расположены в плоскости xOу, то, учитывая, что a_z = b_z = 0, площадь параллелограмма, построенного на этих векторах, равна⁸⁰:

|[ab]| = .

Значит, объем трехмерного параллелепипеда, построенного на трех векторах, равен модулю определителя, по строкам которого стоят координаты трех образующих векторов, а объем (площадь) двумерного параллелепипеда (параллелограмма), построенного на двух векторах, равен модулю аналогично сконструированного определителя второго порядка. Естественное обобщение: геометрический смысл модуля определителя n-го порядка  это объем n-мерного параллелепипеда, построенного на строках (столбцах) определителя. Знак определителя позволяет различать «левые» и «правые» ориентации систем векторов⁸¹.