3.3 Расчет подогревателя

3.3.1 Постановка задачи

Н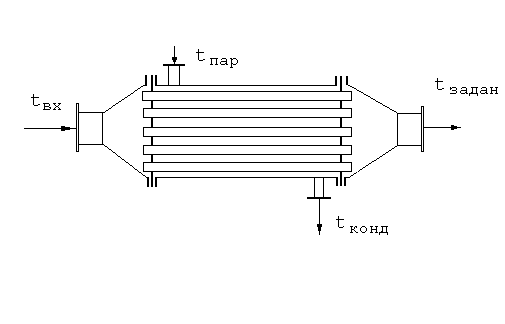 агревание технологических веществ производится чаще всего в кожухотрубчатых аппаратах (подогревателях).

Рис. 3.4 – Схема подогревателя.

Требуемая поверхность нагрева определяется количеством тепла Q, которое необходимо передать от конденсирующегося пара через трубки потоку газа (или жидкости), находящемуся в трубках. При заданном диаметре трубок и их количестве поверхность F теплопередачи линейно зависит от длины трубок:

F=π∙d∙l∙n,

где d – средний диаметр трубок, м;

l – длина трубок, м;

n – количество трубок .

Структура потоков в трубках подогревателя (рис. 3.4) близка к модели идеального вытеснения, а в межтрубном пространстве температура постоянна и равна температуре конденсации пара (t_п).

3.3.2 Вывод математического описания

Вывод математического описания для подогревателя ничем не отличается от теплообменника, поэтому приведем лишь конечное выражение с учетом того, что поверхность теплообмена в этом случае будет определяться количеством трубок в аппарате:

F = П∙d∙l∙n_тр, (11)

где F – поверхность теплообмена;

П – смоченный периметр, м;

d – диаметр внутренней трубы, м;

l – длина аппарата, м;

n_тр – количество трубок.

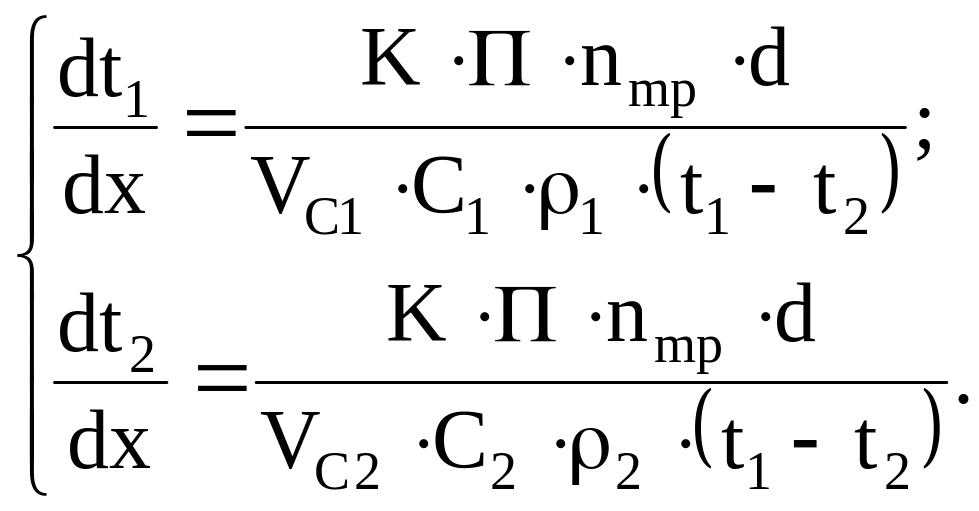(12)

где C₁,C₂ – теплоемкости теплоносителей, Дж/кг·К;

ρ₂, ρ₂– плотности теплоносителей, кг/м³;

К – коэффициент теплопередачи,Вт/(м²· °С);

Vc₁, Vc₂ – объемные расходы горячего и холодного теплоносителей, м³/c;

Следует отметить, что температура горячего теплоносителя постоянна по длине подогревателя, поэтому второе уравнение обращается в нуль и теряет смысл:

(13)

Эта задача может быть решена не только методом RK-4, но также и аналитическим методом. Для установившегося режима работы подогревателя математическое описание теплопереноса имеет вид:

, (14)