3.2 Расчет теплообменника

3.2.1 Постановка задачи

С целью использования вторичных энергоресурсов на химических заводах находит широкое применение теплообменная аппаратура. В теплообменниках различной конструкции происходит передача тепла от горячего технологического вещества к холодному.

Целью работы является составление математической модели аппарата и её дальнейшее исследование с получением зависимости распределения температуры по длине при различных расходах теплоносителей и вида их движения (прямоток и противоток).

3.2.2 Вывод математического описания

Для теплообменника типа „труба в трубе” (рис. 3.3), структура потока близка к идеальному вытеснению (для обоих теплоносителей). Тогда математическое описание можно записать в виде:

(8)

где W₁,W₂ – линейные скорости движения горячего и холодного теплоносителей, м/c (векторные величины, знак которых зависит от направления движения);

Q – количество переданного тепла, Вт;

V₁,V₂ – объемы горячего и холодного теплоносителей в теплообменнике, м³;

C₁,C₂ – теплоемкости теплоносителей, Дж/кг·К;

ρ₂, ρ₂ – плотности теплоносителей, кг/м³.

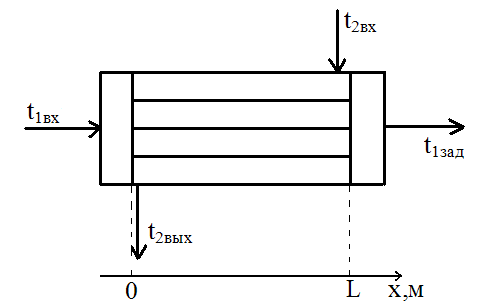
Рис. 3.3 – Схема теплообменника.

Если направление движения противоположно направлению оси X, то знак W – отрицательный.

Без учета потерь в установившемся режиме, уравнения принимают следующий вид:

(9)

Введя известные соотношения:

Q=K·F·(t₁ – t₂);

F=П·d·l;

W=Vc/S;

V=S·l,

где S – площадь сечение для прохода теплоносителя, м²;

l – длина теплообменника, м;

К – коэффициент теплопередачи,Вт/(м²·К);

П – смоченный периметр, м;

Vc – объемный расход теплоносителя, м³/c;

d – диаметр внутренней трубы, м,

получим математическое описание теплообменника (для противотока):

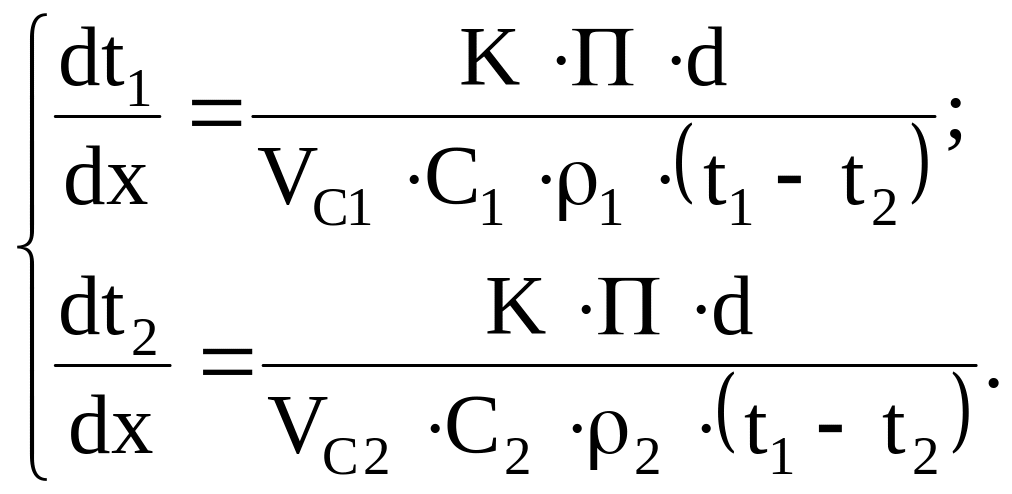(10)

Решая эту систему дифференциальных уравнений при соответствующих условиях однозначности, можно получить распределение температур теплоносителей по длине теплообменника. Для случая прямотока во втором уравнении следует в правой части поставить знак плюс.

3.2.3 Условия однозначности

1. Начальные условия характеризуют значения технологических параметров в начальный момент времени (при τ=0) в любой точке объекта. При этом значение технологических параметров зависит от способа запуска или останова объекта. Так, например, если перед началом работы аппарат был пуст, и в момент времени τ=0 одновременно подали оба теплоносителя, то распределение температур будет следующим (прямоток):

t₁(τ=0, х=0) = 120, ºС t₂(τ=0, х=0) = 30, ºС

t₁(τ=0, х=L) = t_ср, ºС t₂(τ=0, х=L) = t_ср, ºС

В стационарном режиме, который рассматривается в данной задаче, эти условия не имеют смысла.

2. Граничные условия первого рода (ГУ-I) характеризуют значение технологических параметров на границах объекта в любой момент времени. При прямотоке:

t₁(τ, х=0) = 120, ºС t₂(τ, х=0) = 25, ºС

t₁(τ, х=L) = t_зад, ºС t₂(τ, х=L) = 60, ºС

При противотоке:

t₁(τ, х=0) = 120, ºС t₂(τ, х=0) = 60, ºС

t₁(τ, х=L) = t_зад, ºС t₂(τ, х=L) = 25, ºС

где (х=L) определяет координату выхода из аппарата.

3. Граничные условия второго рода (ГУ-II) определяют значения плотностей потоков энергии на границах объекта, характеризующихся законом Фурье:

q_λ = - ,

где λ – коэффициент теплопроводности, Вт/(м·К)

– градиент температур, ºС/м.

Поскольку потери в окружающую среду не учтены в математическом описании, то для рассматриваемого процесса в связи с отсутствием градиента, ГУ-II не имеют смысла.

4. Граничные условия третьего рода (ГУ-III) определяют равенство плотностей потоков тепла на границах раздела двух разнородных фаз.

Как известно, на границе соприкосновения фаз возникает псевдонеподвижный слой теплоносителя. Внутри этого слоя тепло передаётся на молекулярном уровне (теплопроводностью):

q_λ = -

В движущемся слое перенос тепла происходит на молярном уровне по закону Ньютона (плотность потока пропорциональна движущей силе):

q_α = α(t-t_пл)

При равенстве потоков можно записать:

= α(t- t_пл),

где t_пл –значение температуры в приведенной пленке, ºС.

Граничные условия третьего рода позволяют получить при формальном делении правой части равенства на левую безразмерное соотношение (число Нуссельта), показывающее соотношение интенсивностей конвективного и кондуктивного переноса тепла. Следовательно, число Нуссельта также может быть отнесено к граничным условиям третьего рода.

5. Граничные условия четвертого рода (ГУ-IV) характеризуются равенством плотностей потоков тепла на границе раздела двух одинаковых фаз (газ-газ, жидкость-жидкость, твердое-твердое), передаваемых на молекулярном уровне. Форма записи ГУ-IV следующая:

λ₁ dt₁ /dx = λ₂ dt₂ /dx.

6. Геометрические условия задают размеры аппарата и отдельных его элементов (диаметр сечения, по которому движется поток технологического вещества, длина пути, размеры трубок и т.д.).

7. Теплофизические условия определяют свойства технологических веществ: плотности (кг/м³), теплопроводности (Вт/(м*ºС)), теплоемкости (Дж/(кг*ºС)).

8. Кинетические условия определяют линейные скорости движения технологических веществ (W), массовые и объемные скорости (Vc), коэффициенты скоростей процессов (K), коэффициенты теплопроводности (λ).