3.1.2 Вывод математического описания

Математическое описание для нестационарных условий проведения процесса имеет вид:

(1)

где R_i,j – суммарная скорость по j-му компоненту в i-м реакторе;

n – количество реакторов в каскаде;

m – количество реагирующих веществ.

Допустим, в каскаде реакторов в изотермических условиях протекает химическая реакция:

А ^к1 В ^к2 С

Необходимо для установившегося режима определить количество реакторов в каскаде, при котором выход продукта В был бы максимальным, а выход побочного продукта С возможно меньшим.

Для данного химического процесса в стационарных условиях работы математическое описание будет иметь вид:

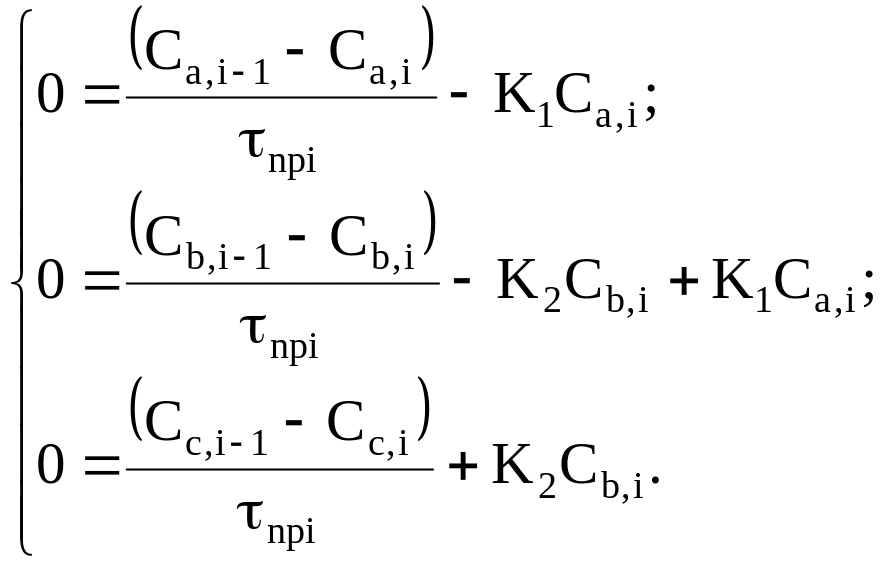(2)

Преобразуем систему (2), разделив дроби почленно:

(3)

Решаем эту систему относительно концентраций реагирующих веществ:

(4)

Таким образом может быть вычислена концентрация реагирующих веществ вначале в первом реакторе, а затем во втором и т.д. Сравнивая концентрацию компонента В в очередном реакторе с концентрацией в предыдущем можно найти такое количество реакторов в каскаде, при котором выход продукта В будет наибольшим. Варьируя величиной констант K₁ и K₂, а также временем пребывания (τ_{пр i}) в реакторах каскада, можно провести исследования работы ячеечной модели и найти наилучший вариант работы.

Систему линейных уравнений (3) можно решить методом Гаусса, но для этого надо привести её к виду:

A · X = B, (5)

где А – двумерный массив коэффициентов при неизвестных;

Х – одномерный массив текущих концентраций;

В – одномерный массив свободных членов.

(6)

Сгруппируем слагаемые, содержащие одинаковые концентрации и получим:

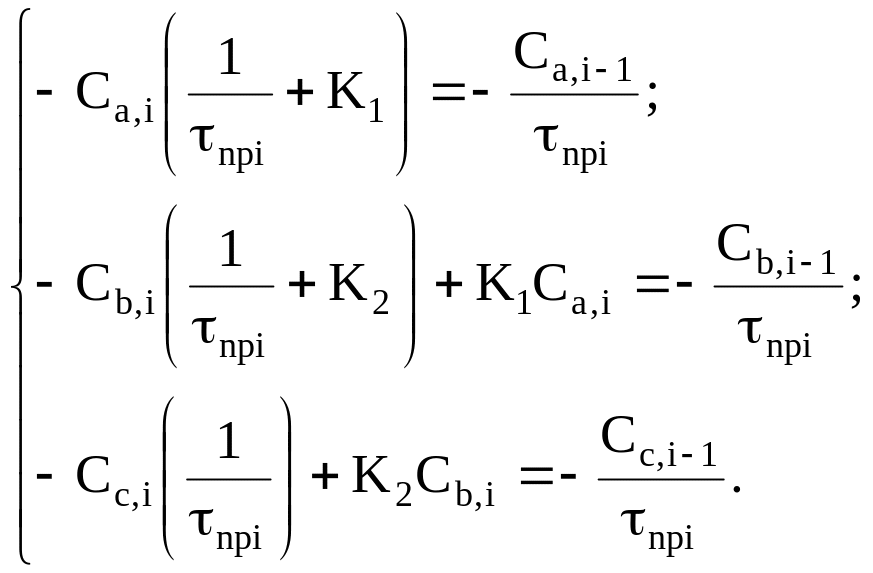(7)

Представим полученную систему линейных уравнений в виде табл. 3.1.

Таблица 3.1 – Таблица массивов

Массив А			Массив В	Массив Х
Ca	Cb	Cc
	0	0		Ca,i
K1		0		Cb,i
0	K2			Cc,i

3.1.3 Условия однозначности

Для „привязки” математического описания к реальному объекту необходимо определить значения многих переменных, в соответствии с конструкцией конкретного аппарата и условиями его работы. Для этих целей используют условия однозначности (УО), состоящие из:

1. Начальные условия характеризуют значения технологических параметров в начальный момент времени (при τ=0) в любой точке объекта. При этом значение технологических параметров зависит от способа запуска или останова объекта. Так, например, если перед началом работы ячеечный реактор был заполнен реакционной смесью и в момент времени τ=0 созданы условия для протекания реакции (например, температурные условия), то распределение концентраций будет следующим:

С_a(τ=0, х=0) = 100 % С_a(τ=0, х>0) = 100 %

C_b(τ=0, х=0) = 0 % C_b(τ=0, х>0) = 0 %

C_c(τ=0, х=0) = 0 % C_c(τ=0, х>0) = 0 %

Если же вначале аппарат был пуст, а в момент времени τ=0 в него подали реакционную смесь и создали условия для протекания реакции, то распределение концентраций будет следующим:

С_a(τ=0, х=0) = 100 % С_a(τ=0, х>0) = 0 %

C_b(τ=0, х=0) = 0 % C_b(τ=0, х>0) = 0 %

C_c(τ=0, х=0) = 0 % C_c(τ=0, х>0) = 0 %

2. Граничные условия первого рода (ГУ-I) характеризуют значение технологических параметров на границах объекта в любой момент времени:

С_a(τ, х=0) = 100 % С_a(τ, х=L) = 0 %

C_b(τ, х=0) = 0 % C_b(τ, х=L) = 0 %

C_c(τ, х=0) = 0 % C_c(τ, х=L) = 0 %

где (х=L) определяет координату выхода из аппарата.

3. Граничные условия второго рода (ГУ-II) определяют значения плотностей потоков масс или энергии на границах объекта, характеризующихся соответственно законами Фика и Фурье:

q_D = -D , q_λ = - ,

где D – коэффициент диффузии, м/с ;

λ – коэффициент теплопроводности, м² ºС/м.

, – соответственно градиенты концентраций и температур.

Для рассматриваемого процесса в связи с отсутствием градиента ГУ-II не имеют смысла.

4. Граничные условия третьего рода (ГУ-III) определяют равенство плотностей потоков масс или энергии на границах раздела двух разнородных фаз (см. рис. 3.2).

Как известно, на границе соприкосновения фаз возникает псевдонеподвижный слой теплоносителя или газа в абсорбере (приведенный слой). Внутри этого слоя тепло или масса передаются на молекулярном уровне (теплопроводностью или диффузией):

q_D = -D , q_λ = -

В движущемся слое перенос тепла или массы происходит на молярном уровне по закону Ньютона (плотность потока пропорциональна движущей силе):

q_β = β(С-С^*), q_α = α(t-t_пл)

При равенстве потоков можно записать:

D = β(С- С^*), = α(t- t_пл) ,

где С^* и t_пл –значение концентрации и температуры в приведенной пленке.

Граничные условия третьего рода позволяют получить при формальном делении правой части равенства на левую безразмерное соотношение (число Нуссельта), показывающее соотношение интенсивностей конвективного и кондуктивного переноса тепла. Следовательно, число Нуссельта также может быть отнесено к граничным условиям третьего рода. Для данного процесса в связи с отсутствием процесса массопереноса ГУ-III не имеют смысла.

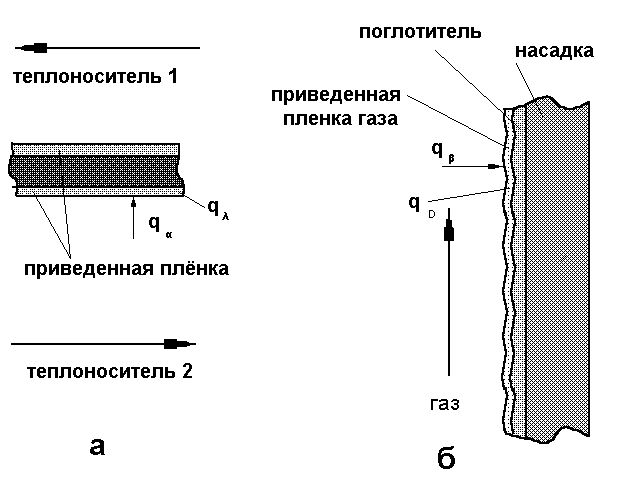
Рис 3.2. – Иллюстрация к граничным условиям третьего рода (а – теплообменные процессы; б – массообменные процессы).

5. Граничные условия четвертого рода (ГУ-IV) характеризуются равенством плотностей потоков массы или энергии на границе раздела двух одинаковых фаз (газ-газ, жидкость-жидкость, твердое-твердое), передаваемых на молекулярном уровне. Форма записи ГУ-IV следующая:

D₁ ¹ = D₂ ², λ₁ dt₁ /dx = λ₂ dt₂ /dx.

Для рассматриваемого процесса ГУ-IV не имеют смысла.

6. Геометрические условия задают размеры аппарата и отдельных его элементов (диаметр сечения, по которому движется поток технологического вещества, длина пути, размеры трубок, насадки и т.д. и т.п.).

7. Теплофизические условия определяют свойства технологических веществ: плотности (кг/м³), теплоемкости (Дж/кг град), теплопроводности (Дж/(м² град/м)), коэффициенты диффузии (м²/с) и т.д.

8. Кинетические условия определяют линейные скорости движения технологических веществ, массовые и объемные скорости, коэффициенты скоростей процессов (коэффициенты тепло- и массообмена, коэффициенты скоростей химических реакций и т.д.).