3.5.2 Вывод математического описания

Математическое описание процесса абсорбции в стационарных условиях может быть представлено системой уравнений:

(36)

где W₁– скорость движения газа по свободному сечению насадки, м/c;

W₂ – скорость стекания жидкого поглотителя по насадке, м/c;

V₁– свободный объем насадки, м³;

V₂ – суммарный объем стекающей жидкости (объем всех пленок), м³;

G – количество поглощаемого компонента, кг/с;

y – концентрация компонента в газовой фазе, г/м³;

x – концентрация компонента в жидкой фазе, г/л.

В связи со сложностью определения объема стекающей жидкости и скорости её стекания производим ряд преобразований. Так, объем поглотителя, стекающего по насадке, может быть представлен:

V₂=S_ж.пл*H, (37)

где S_ж.пл – площадь сечения всех пленок по насадке, м²;

H – рабочая высота насадки, м.

Объем газа в свободном пространстве рабочей части абсорбера:

V₁ =S_св*H, (38)

где S_св – площадь свободного сечения насадки, м².

Количество поглощаемого компонента:

G=K_yF(y-y*), (39)

где K_y – коэффициент массообмена;

F – поверхность насадки, м² (F=PH);

y*- равновесная концентрация компонента на границе раздела фаз, г/м3.

y*=mx, (40)

где m – константа фазового равновесия.

Подставив все принятые обозначения в систему уравнений (36), получим:

(41)

Но, так как вектор скорости направлен навстречу потоку газа, то знак у скорости будет отрицательный, поэтому после деления уравнений системы 1-го на W₁, а 2-го на W₂ и, учитывая, что произведение скорости на сечение потока дает нам объемный расход (V₁ и V₂ соответственно), то система уравнений (41) будет иметь вид:

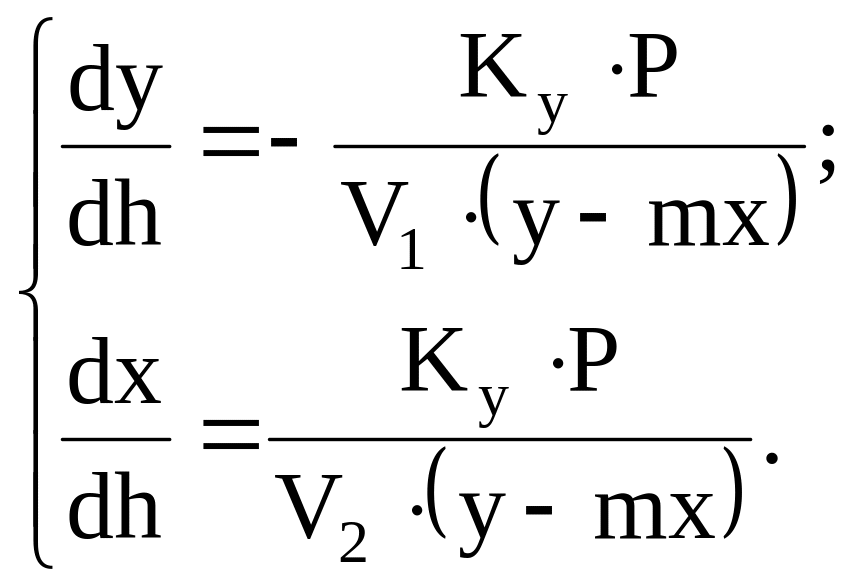(42)

при принятых условиях:

y(h=0)=y_вх – концентрация компонента в газе на входе в абсорбер;

x(h=0)=x_вых – концентрация компонента в насыщенном поглотителе.

3.5.3 Условия однозначности

1. Начальные условия характеризуют значения технологических параметров в начальный момент времени (при τ=0) в любой точке объекта. При этом значение технологических параметров зависит от способа запуска или останова объекта.

В стационарном режиме, который рассматривается в данной задаче, эти условия не имеют смысла.

2. Граничные условия первого рода (ГУ-I) характеризуют значение технологических параметров на границах объекта в любой момент времени.

y₁(τ, х=0) = y_вх, г/м³ x₂(τ, х=0) = x_вых, г/л

y₁(τ, х=H) = y_вых, г/м³ x₂(τ, х=H) = x_вх, г/л

где (х=H) определяет координату выхода из аппарата.

3. Граничные условия второго рода (ГУ-II) определяют значения плотностей потоков вещества на границах объекта, характеризующихся законом Фурье:

q_D= - ,

где D – коэффициент диффузии, м²/с;

– градиент концентрации, кг/м³.

Поскольку потери в окружающую среду не учтены в математическом описании, то для рассматриваемого процесса в связи с отсутствием градиента, ГУ-II не имеют смысла.

4. Граничные условия третьего рода (ГУ-III) определяют равенство плотностей потоков вещества на границах раздела двух разнородных фаз.

Как известно, на границе соприкосновения фаз возникает псевдонеподвижный слой вещества. Внутри этого слоя вещество передаётся на молекулярном уровне (диффузией):

q_D= - ,

В движущемся слое перенос вещества происходит на молярном уровне по закону Ньютона (плотность потока пропорциональна движущей силе):

q_β = β(y-y^*).

При равенстве потоков можно записать:

- = β(y-y^*),

где y^* – значение равновесной концентрации в приведенной пленке г/м³.

Граничные условия третьего рода позволяют получить при формальном делении правой части равенства на левую безразмерное соотношение (число Нуссельта), показывающее соотношение интенсивностей конвективного и кондуктивного переноса тепла. Следовательно, число Нуссельта также может быть отнесено к граничным условиям третьего рода.

5. Граничные условия четвертого рода (ГУ-IV) характеризуются равенством плотностей потоков вещества на границе раздела двух одинаковых фаз (газ-газ, жидкость-жидкость, твердое-твердое), передаваемых на молекулярном уровне. Форма записи ГУ-IV следующая:

=

6. Геометрические условия задают размеры аппарата и отдельных его элементов (высота и диаметр аппарата, высота яруса насадки).

7. Теплофизические условия определяют свойства технологических веществ: концентрация компонента в газе, жидкости.

8. Кинетические условия: объемные скорости (V, L), коэффициент массообмена (K_у), коэффициент фазового распределения (m).