3.4.7 Варианты заданий
Таблица 3.9 – Варианты заданий
№ |
L, м |
H, м |
tвозд, °С |
tпечи, °С |
δст1, мм |
δст2, мм |
λст1, Вт м·К |
λст2, Вт м·К |
λиз, Вт м·К |
λ, Вт м·К |
μ·106, Па·с |
ρ, кг м3 |
1 |
5 |
2 |
-10 |
400 |
5 |
20 |
46.5 |
0.80 |
0.098 |
0.030 |
12 |
0.40 |
2 |
10 |
3 |
-5 |
500 |
6 |
60 |
40.8 |
0.80 |
0.200 |
0.028 |
9 |
0.34 |
3 |
12 |
4 |
0 |
600 |
7 |
12 |
45.0 |
0.65 |
0.150 |
0.032 |
10 |
0.34 |
4 |
20 |
5 |
5 |
650 |
7 |
40 |
46.3 |
0.70 |
0.110 |
0.035 |
11 |
0.35 |
5 |
25 |
2 |
10 |
700 |
5 |
53 |
43.6 |
0.65 |
0.130 |
0.033 |
12 |
0.37 |
6 |
30 |
3 |
15 |
750 |
5 |
80 |
41.2 |
0.75 |
0.090 |
0.029 |
10 |
0.36 |
7 |
35 |
4 |
20 |
800 |
400 |
50 |
1.05 |
0.50 |
0.140 |
0.037 |
11 |
0.33 |
8 |
40 |
5 |
-15 |
850 |
270 |
40 |
1.58 |
0.75 |
0.170 |
0.036 |
13 |
0.34 |
9 |
45 |
3 |
-10 |
950 |
350 |
60 |
1.32 |
0.80 |
0.150 |
0.033 |
9 |
0.35 |
10 |
50 |
2 |
-5 |
1000 |
400 |
65 |
1.30 |
0.73 |
0.120 |
0.031 |
11 |
0.37 |
11 |
50 |
4 |
0 |
1100 |
045 |
50 |
0.95 |
0.81 |
0.100 |
0.029 |
12 |
0.30 |
12 |
40 |
4 |
5 |
1200 |
500 |
55 |
0.90 |
0.77 |
0.130 |
0.030 |
10 |
0.29 |
По технике безопасности температура на поверхности изоляции не должна превышать 40°С.
7 Расчет насадочного абсорбера
7.1 Постановка задачи
В химической технологии абсорбция широко применяется для выделения из газовых смесей ценных компонентов (например, для извлечения из коксового газа аммиака, бензольных углеводородов, сероводорода и др.), для очистки технологических и горючих газов от вредных примесей, для санитарной очистки газов и т.д.
Насадочные абсорберы (рис.3.6) представляют собой цилиндрические колонны, заполненные (с целью увеличения поверхности контакта газа и жидкого поглотителя) насадкой. В качестве насадки часто используются тонкостенные кольца, деревянные доски, собранные в пакеты, и др.
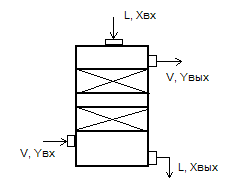
Рис 3.6 – Схема насадочного абсорбера
Жидкий поглотитель стекает по поверхности насадочного абсорбера тонкой пленкой. Следовательно, структура потока его близка к модели идеального вытеснения.
Газ поступает в колонну снизу и движется вверх по свободному сечению насадки противотоком по отношению к жидкости. Структура потока газа по узким каналам также может быть принята как модель идеального вытеснения.