
- •Введение
- •Литература
- •Свойства операций над множествами
- •2.2 Законы логики
- •1. Закон исключённого третьего:
- •Соответствия
- •Отношения
- •3.1. Отношение эквивалентности
- •3. 2. Отношения порядка
- •4. Бесконечные множества
- •4.1.Теоремы о счётных множествах
- •4.2. Несчётные множества
- •4.4. Трансфинитная индукция
- •6. Проблемы наивной теории множеств
- •6.1. Кризисы в математике
- •6.2. Проблема континуума и континуум-гипотеза
- •6.3. Аксиома выбора и парадоксы наивной теории множеств.
- •Культурный минимум.
- •Вопросы.
- •Задачи.
Отношения
Не относитесь к себе слишком всерьёз.
Пятое правило Черчилля.
(первых четырёх не существует)
Комментарий. Соотношения между элементами одного и того же множества называются отношениями. Отношения характеризуются иным перечнем свойств, нежели соответствия.
Определение
1.
На некотором множестве
задано отношение 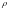 ,
если для любых двух элементов
,
если для любых двух элементов
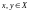 можно сказать, находятся ли они в
отношении
или нет.
можно сказать, находятся ли они в
отношении
или нет.
Комментарий.
Можно
сказать, что отношение
есть отображение
: 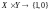 ,
где значение 1 соответствует «истине»,
а значение 0 — «лжи» (здесь важен
порядок, в котором берутся элементы
,
где значение 1 соответствует «истине»,
а значение 0 — «лжи» (здесь важен
порядок, в котором берутся элементы
 и
и
 ).
).
Определение
2.
Отношение
рефлексивно, если
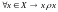 .
.
Комментарий. То есть отношение применимо к самому объекту. Например, отношение включения. Поскольку любое множество включено само в себя, то отношение включения обладает свойством рефлексивности. Отношение «спасения» на множестве утопающих – рефлексивно.
Определение 3. Отношение антирефлексивно, если к самому объекту оно всегда неприменимо.
Например,
«перпендикулярность» на множестве
прямых. Прямая не может быть перпендикулярна
самой себе.
Определение
4.
Отношение
симметрично, если
 .
.
Если
Иванов «учится в одной группе» с Петровым,
то справедливо и обратное.
Определение
5.
Отношение
асимметрично, если
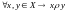 ,
но неверно, что
,
но неверно, что
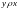 .
Если стольник можно “разменять”
десятками, то обратное сложно.
Определение
6.
Отношение
антисимметрично, если из
.
Если стольник можно “разменять”
десятками, то обратное сложно.
Определение
6.
Отношение
антисимметрично, если из
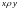 и
следует, что
и
следует, что
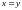 .
Определение
7.
Полнота
отношения означает, что для любой пары
разных элементов данного множества
данное отношение выполнимо на всём
множестве.
.
Определение
7.
Полнота
отношения означает, что для любой пары
разных элементов данного множества
данное отношение выполнимо на всём
множестве.
Например,
отношение “больше или равно” полно
на множестве действительных чисел и не
полно на множестве комплексных.
Определение
8.
Отношение
транзитивно, если из
и
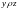 следует, что
следует, что
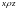 .
.
Комментарий. Если Иванов “учится в одной группе” с Петровым, а Петров с Сидоровым, то Иванов “учится в одной группе” с Сидоровым. Отношение включения тоже транзитивно. Если группа «включена» в множество студентов университета, а это множество «включено» в множество студентов страны, то множество студентов группы «включено» в множество студентов страны. Но если студенческую группу рассматривать как элемент университета, понимаемого как множества, состоящего из групп, а университет рассматривать как элемент высшей школы – множества, состоящего из университетов, то группа не является элементом высшей школы (там элементы университеты). То есть отношение “принадлежности” не транзитивно.
Комментарий. Каждое конкретное отношение обладает совокупностью свойств. Рассмотрим важнейшие группы отношений, у которых совокупности свойств одинаковые.
3.1. Отношение эквивалентности
Определение 1. Отношение, обладающее свойствами рефлексивности, симметричности и транзитивности называется отношением эквивалентности.
Комментарий.
Это,
например, отношение “равенства” чисел,
или отношение “учиться в одной
студенческой группе”, или отношение
изоморфизма. Это
определение избыточно потому, что любое
симметричное и транзитивное отношение
рефлексивно. В самом деле, пусть
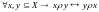 (в силу симметричности). Тогда, в силу
транзитивности, имеет место
(в силу симметричности). Тогда, в силу
транзитивности, имеет место
 .
.
Теорема 1. Отношение эквивалентности разбивает множество на непересекающиеся подмножества классы эквивалентности.

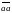 Пусть
Пусть
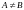 и
и
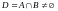 .
То есть
.
То есть
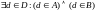 .
Тогда
.
Тогда
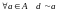 и
и
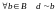 .
Отсюда в силу транзитивности
.
Отсюда в силу транзитивности
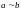 ,
но тогда
,
но тогда
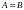 .■
.■
Определение 2. Множество классов эквивалентности данного множества называется фактор-множеством, а операция построения фактор - множества называется факторизацией.
