Методы решения логарифмических неравенств (задания с3 егэ)
Корянов А.Г., Прокофьев А.А.
Основой для написания данной статьи явился анализ заданий материалов МИОО, предлагавшихся в течение двух лет в качестве подготовки к итоговому экзамену, и результаты проверки авторами в качестве экспертов работ ЕГЭ 2010 и 2011 гг.
Надо отдать должное составителям заданий, поскольку при решении логарифмических неравенств в заданиях С3 в диагностических, тренировочных, репетиционных работах и в итоговых вариантах ЕГЭ 2010 и 2011 в основном было достаточно использования стандартных методов. К таковым методам можно отнести:
метод равносильных переходов;
решение неравенства на промежутках;
метод замены;
обобщенный метод интервалов;
Кроме того, в ряде репетиционных работ для решения неравенств использовались нестандартные методы:
метод рационализации;
метод оценки, в частности, использование классических неравенств.
Остановимся на перечисленных выше методах решения.
Метод равносильных переходов
При решении неравенств используют преобразования, при которых множество решений неравенства либо не меняется, либо расширяется (можно получить посторонние решения). Поэтому важно знать, какие преобразования неравенства являются равносильными и при каких условиях.
Начнем с примеров, в которых используются логарифмы с постоянными основаниями.
Неравенства вида
Пусть логарифмическое неравенство удалось свести к виду
,
тогда для дальнейшего решения применяется одна из схем.
Если число
,
то
(1)
Если число
,
то
(2)
При выводе этих схем решения неравенства
используется свойство монотонности
функции
на множестве
.
При
функция возрастающая, при
– убывающая.
Замечание. При решении строгого
неравенства
в схемах (1) и (2) нестрогие неравенства
заменяются строгими.
Пример 1. Решить неравенство
.
Решение. Так как функция
строго возрастает на множестве
,
то данное неравенство можно заменить
равносильной системой
Ответ:
.
Рассмотрим неравенства, в которых присутствуют логарифмы с переменным основанием.
Неравенства вида
Из предыдущего пункта следует, что неравенство указанного вида равносильно совокупности систем неравенств.
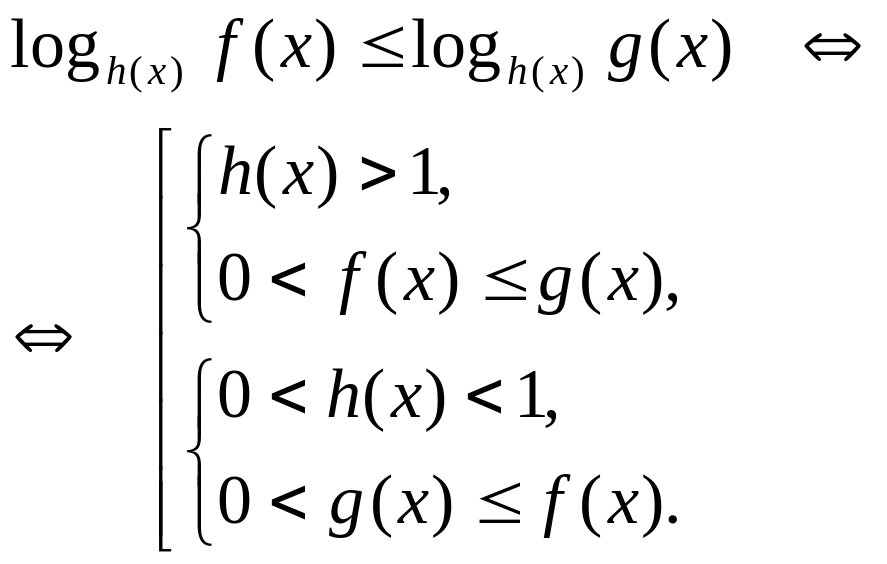(3)
Замечание. При решении строгого
неравенства
в схеме (3) нестрогие неравенства
заменяются строгими.
Пример 2. Решить неравенство
.
Решение. Запишем неравенство в виде
и заменим его равносильной совокупностью двух систем
Р
Рис. 2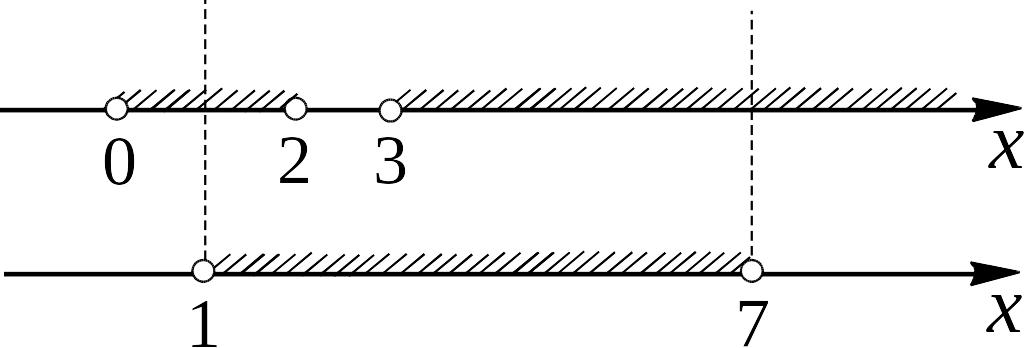
Имеем
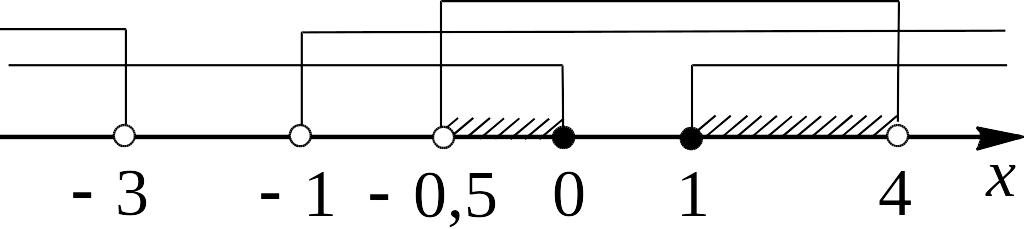
Рис. 1
Отсюда получаем (см. рис. 1) решение (I):
.
Решим систему (II):
Имеем
.
Получаем, что система (II) решений не имеет.
Ответ:
.
Пример 3. (МИОО, 2009). Решить неравенство
.
Решение. Выполняя равносильные переходы, получим, что данное неравенство равносильно следующей системе неравенств
Необходимо рассмотреть только случай, когда основание больше единицы, поэтому полученная система равносильна следующей
На рис. 2 представлена графическая интерпретация получения решения последней системы неравенств.
Ответ:
.