Тема 1.8: " Решение дифференциальных уравнений с разделяющимися переменными первого порядка "

Цель: Решать дифференциальные уравнения с разделяющимися переменными первого порядка.

Теоретический материал:

Дифференциальным уравнением (ДУ) называется такое уравнение, которое содержит производные или дифференциалы от искомой функции, а также может содержать саму искомую функцию и независимые переменные. ДУ называется обыкновенным, если искомая функция зависит только от одной переменной. Говорят, что ДУ имеет порядок n , если в него входят производные (дифференциалы) порядка n и не входят производные (дифференциалы) высших порядков. Общим решением ДУ порядка n называется функция y =y(x, c₁, ..., c_n) от независимой переменной x с n параметрами (константами) c₁, ..., c_n такая, что при любых фиксированных значениях параметров эта функция при подстановке в уравнение обращает последнее в тождество. Задачей Коши называется задача нахождения таких фиксированных значений констант, что в результате искомая функция будет удовлетворять начальным условиям y(x₀) = y₀, y'(x₁) = y₁, ..., Такая функция с фиксированными значениями констант называется частным решением ДУ. ДУ возникают в исследованиях в различных областях человеческой деятельности: в физике, технике, экономике, — практически везде, где применяется дифференциальное исчисление.

Уравнение (1)

где функции f(x), g(y) непрерывны при рассматриваемых значениях x и y, называется ДУ с разделяющимися переменными.

Алгоритм решения.

1. Уравнение (1) может быть записано в виде (2)

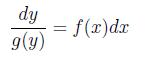
Случай, когда функция g(y) = 0 привел бы нас к уравнению y' = 0, решением которого является y = C.

2. Интегрируем обе части уравнения (2):

получаем общее решение y уравнения (1) (возможно в виде неявной функции).

3. Если дана задача Коши, подставляем начальные условия в формулу общего решения и находим соответствующее частное решение.

Примеры вычисления

Пример 1. Найти общее решение ДУ

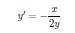
Разделяя переменные, получим:

Затем интегрируем:

откуда

Пример 2. Найти общее решение ДУ

ydx + xdy = 0

Делим обе части равенства на xy:

Интегрируем обе части равенства и получаем

откуда ln |x| + ln|y| = ln|C|.

ln |y| = ln|C| − ln |x|

Потенцируя и избавляясь от модулей, получаем:

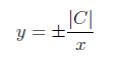
Пример 3. Решить задачу Коши для ДУ

при начальном условии y(0) = π/2 .

Делим обе части уравнения на e^x/sin y (очевидно e^x/sin y# 0):

По определению производной y'= dy/dx :

Домножим обе части равенства на dx:

и проинтегрируем:

_

откуда общее решение (общий интеграл — то есть запись решения в виде неявной функции)

Найдем решение задачи Коши, для чего подставим в общее решение значения x = 0 и y = π/2 :

0 − 1 = C,

откуда

C = −1.

Искомое частное решение (в виде неявной функции):

−cos y + e^−x = −1

или

−cos y + e^−x + 1 = 0.

Задание для практической работы по теме " Решение дифференциальных уравнений с разделяющимися переменными первого порядка "

1. Найти общее решение дифференциального уравнения.

2. Найти частное решение дифференциального уравнения, решив задачу Коши при заданных начальных условиях.

Вариант 1. 1). y' = x²y,

2). y³dx = x²dy, y(1) = 2.

Вариант 2. 1). x²dy + y²dx = 0,

2). y’=(1+y²)/(1+x²), y(0)=1.

Вариант 3. 1). y' = 2y e^x,

2). e^xyy' = e^x+1, y(0) = 1.

Вариант 4. 1). (1 + y²)dx + (1+x²)dy = 0,

2). xy’-(x+1)/y=0, y(1)=0.

Практическое занятие №9