Тема 4.4: "Вычисление интегралов по формулам прямоугольников".

Цель: Вычислять определенный интеграл приближенно методом прямоугольников.

Теоретический материал:

Введение. Пусть требуется найти определенный интеграл от непрерывной функции ƒ(х). Если можно найти первообразную F(x) функции ƒ(х), то интеграл вычисляется по формуле Ньютона-Лейбница:

Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция у = ƒ(х) задана графически или табличнo) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.

Рассмотрим две наиболее употребительные формулы приближенного вычисления определенного интеграла — формулу прямоугольников и формулу трапеций, основанные на геометрическом смысле определенного интеграла.

Формула прямоугольников. Пусть на отрезке [а; b], а < b, задана непрерывная функция ƒ(х). Требуется вычислить интеграл, численно равный площади соответствующей криволинейной трапеции.

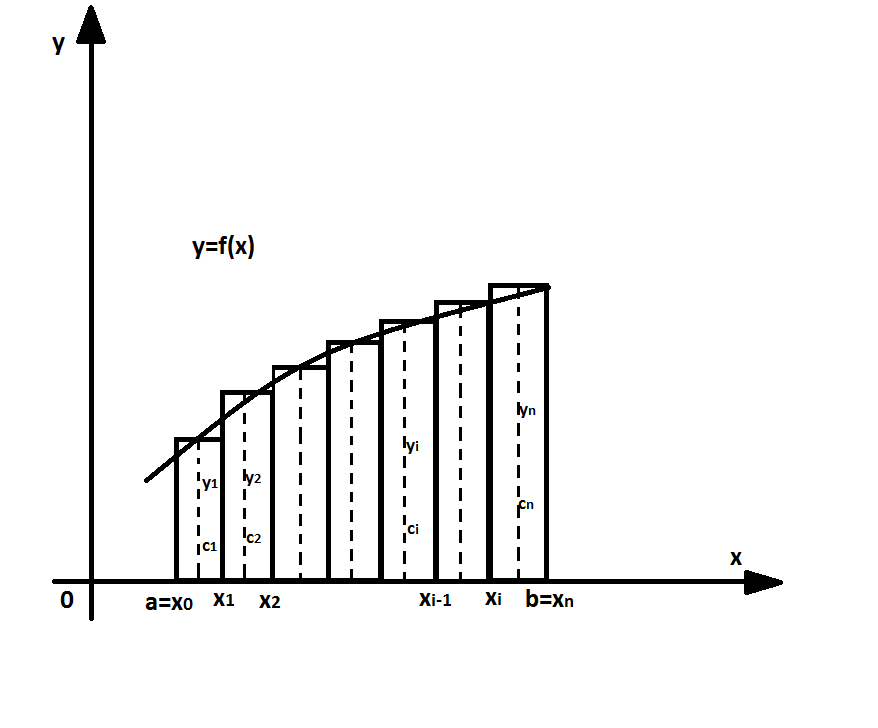
Разобьем основание этой трапеции, т. е. отрезок [а; b], на n равных частей (отрезков) длины (шаг разбиения) с помощью точек х₀= а, x₁, х₂,..., х_n = b. Можно записать, что х_i= х₀+h·i, где i = 1,2,..., n

В середине каждого такого отрезка построим ординату ŷ_i =ƒ(с_i) графика функции у = ƒ(х). Приняв эту ординату за высоту, построим прямоугольник с площадью h · ŷ_i.

Тогда сумма площадей всех n прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла

Эта формула называется формулой средних прямоугольников

Пример вычисления

Вычислить методом прямоугольников интеграл , разбив отрезок интегрирования [0; 2] на 4 части.

Решение: Имеем: ƒ(х) = х^3,

по формуле прямоугольников:

Точное значение интеграла

А бсолютная погрешность равна 0,125.

Задание для практической работы по теме «Вычисление интегралов по формулам прямоугольников».

Дан интеграл . Вычислить:

1). интеграл методом прямоугольников, где a- порядковый № студента по журналу, b=a+2. Разбить отрезок интегрирования на 8 частей.

2). интеграл точно.

3). абсолютную погрешность.

Практическая работа № 20

Тема 4.5: " Вычисление интегралов по формулам трапеций ".

Цель: Вычислять определенный интеграл приближенно методом трапеций.

Теоретический материал:

Формула трапеций. Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Разобьем отрезок [а; b] на n равных частей длины Абсциссы точек деления а = х₀, x₁,х₂,...,b = х_n.

Пусть у₀,у₁...,у_n —соответствующие им ординаты графика функции. Тогда расчетные формулы для этих значений примут вид х_i = a+h*i, у_i=ƒ(x_i), i= 0,1,2,..., n; Заменим кривую у=ƒ(х) ломаной линией, звенья которой соединяют концы ординат y_i и y_i+1 (i = 0,1,2,.. .,n). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями у_i, y_i+1 и высотой

или

Эта формула называется формулой трапеций.

Пример вычисления.

Вычислить методом трапеций интеграл , разбив отрезок интегрирования [0; 2] на 4 части.

Решение: Имеем: ƒ(х) = х^3,

Т очное значение интеграла

Абсолютная погрешность равна 0,25.

Задание для практической работы по теме «Вычисление определенного интеграла приближенно методом трапеций»

Дан интеграл . Вычислить:

1). интеграл методом трапеций, где a- порядковый № студента по журналу, b=a+2. Разбить отрезок интегрирования на 8 частей.

2). интеграл точно.

3). абсолютную погрешность.