
- •131018.51 « Разработка и эксплуатация нефтяных и газовых месторождений»
- •Аннотация
- •Введение
- •Раздел 1. Дифференциальное и интегральное исчисление.
- •Тема 1.1: «Вычисление производных функций».
- •Теоретический материал.
- •Правила дифференцирования:
- •Примеры вычисления производных.
- •Тема 1.2: «Нахождение углового коэффициэнта касательной к графику функции в указанной точке. Составление уравнения касательной.»
- •Теоретический материал:
- •Геометрический смысл производной функции в точке.
- •Составление уравнения касательной прямой
- •Тема 1.3: «Вычисление производных сложных функций».
- •Теоретический материал:
- •Примеры вычисления производных сложных функций.
- •Тема 1.4:«Вычисление производных высших порядков функции нескольких переменных».
- •Теоретический материал: Производные высшего порядка.
- •Тема 1.5:«Нахождение табличных интегралов. Вычисление интегралов с использованием их свойств и таблицы интегралов».
- •Теоретический материал:
- •Тема 1.6: «Применение формулы Ньютона-Лейбница, свойства определенного интеграла при вычислениях. Методы интегрирования по частям и подстановкой».
- •Теоретический материал: Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.
- •Формула интегрирования по частям:
- •Определенный интеграл
- •Примеры вычисления
- •Тема 1.7: «Геометрический смысл определенного интеграла. Вычисление площади плоской фигуры с помощью определенного интеграла»
- •Теоретический материал:
- •Тема 1.8: " Решение дифференциальных уравнений с разделяющимися переменными первого порядка "
- •Теоретический материал:
- •Примеры вычисления
- •Тема 1.9: "Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами"
- •Теоретический материал:
- •Алгоритм решения
- •Примеры вычисления
- •Тема 1.10: «Нахождение решения дифференциальных уравнений Бернулли».
- •Теоретический материал:
- •Примеры вычисления.
- •Раздел 2. Числовые ряды
- •Тема 2.1: «Вычисление членов числового ряда. Вычисление частичных сумм».
- •Теоретический материал:
- •Примеры вычисления
- •Задание для практической работы по теме «Вычисление членов числового ряда. Вычисление частичных сумм».
- •Тема 2.2: «Применение необходимого и достаточного признаков сходимости числовых рядов и признака Даламбера»
- •Теоретический материал:
- •Примеры вычисления
- •Тема 2.3: «Выделение знакоположительного, знакочередующегося и степенного ряда. Разложение элементарных функций по формуле Тейлора».
- •Теоретический материал:
- •Примеры вычислений
- •Понятие функционального ряда
- •Примеры вычислений
- •Разложение элементарных функций в ряд Маклорена
- •Раздел 3. ОСновы дискретной математики.
- •Тема 3.1: «Выполнение операций над множествами».
- •Тема 3.2: «определение основных характеристик графа».
- •Теоретический материал:
- •Раздел 4. Численное дифференцирование и интегрирование.
- •Теоретический материал
- •Теоретический материал:
- •Примеры вычислений
- •Тема 4.3: "Приближенное вычисление значения функции y(X) в точке с помощью производной".
- •Теоретический материал:
- •Пример вычисления
- •Тема 4.4: "Вычисление интегралов по формулам прямоугольников".
- •Теоретический материал:
- •Пример вычисления
- •Тема 4.5: " Вычисление интегралов по формулам трапеций ".
- •Теоретический материал:
- •Список литературы
Примеры вычислений
Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
Пример1.
![]() ;
;
Решение.
Члены данного ряда по абсолютной величине монотонно убывают:
![]() и
и
![]()
Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
Ряд
![]() ,
составленный из абсолютных величин
данного ряда, является гармоническим
рядом, который, расходится. Поэтому
данный ряд сходится условно.
,
составленный из абсолютных величин
данного ряда, является гармоническим
рядом, который, расходится. Поэтому
данный ряд сходится условно.
Пример
2.
![]()
Решение.
Члены данного ряда по абсолютной величине монотонно убывают:
![]() ,
но
,
но
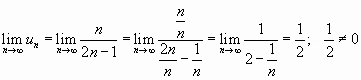 .
.
Ряд расходится, так как признак Лейбница не выполняется.
Пример
3.
![]() ;
;
Решение.
Используя признак Лейбница, получим
![]() ;
;![]() ,
,
т.е. ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
![]() .
.
Это геометрический
ряд вида![]() ,
где
,
где![]() ,
который сходится. Поэтому данный ряд
сходится абсолютно.
,
который сходится. Поэтому данный ряд
сходится абсолютно.
Пример
4.
![]() ;
;
Решение.
Используя признак Лейбница, имеем
![]() ;
;
![]() ,
т.е. ряд сходится.
,
т.е. ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
![]() ,
или
,
или
 .
.
Это обобщенный
гармонический ряд, который расходится,
так как![]() .
Следовательно, данный ряд сходится
условно.
.
Следовательно, данный ряд сходится
условно.
Понятие функционального ряда
Ряд, членами которого являются функции от х, называется функциональным:
![]() .
.
Придавая х
определенное
значение
![]() ,
получим числовой ряд
,
получим числовой ряд
![]() ,
,
который может быть как сходящимся, так и расходящимся.
Если полученный числовой ряд сходится, то точка называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда.
Совокупность
числовых значений аргумента
![]() ,
при которых функциональный ряд сходится,
называется его областью
сходимости.
,
при которых функциональный ряд сходится,
называется его областью
сходимости.
В области сходимости
функционального ряда его сумма является
некоторой функцией от
:![]() .
.
Определяется она в области сходимости равенством
![]() ,
где
,
где
![]() -
частичная сумма ряда.
-
частичная сумма ряда.
Пример 5.
Найти область сходимости ряда
![]() .
.
Решение.
Данный ряд является рядом геометрической
прогрессии со знаменателем
![]() .
Следовательно, этот ряд сходится при
.
Следовательно, этот ряд сходится при
![]() ,
т.е. при всех
,
т.е. при всех
![]() ;
сумма ряда равна
;
сумма ряда равна
![]() ;
;
![]() ,
при
.
,
при
.
Степенным рядом называется ряд вида
![]() ,
,
где числа
![]() называются
коэффициентами
ряда, а
член
называются
коэффициентами
ряда, а
член
![]() -
общим членом ряда.
-
общим членом ряда.
Областью сходимости степенного ряда называется множество всех значений , при которых данный ряд сходится.
Число![]() называется радиусом
сходимости
степенного ряда, если при
называется радиусом
сходимости
степенного ряда, если при
![]() ряд
сходится и притом абсолютно, а при
ряд
сходится и притом абсолютно, а при
![]() ряд
расходится.
ряд
расходится.
Радиус сходимости найдем, используя признак Даламбера:
 (
не
зависит от
),
(
не
зависит от
),
 ,
,
т.е. если степенной
ряд сходится при любых
,
удовлетворяющих данному условию и
расходится при
 .
.
Отсюда следует, что если существует предел

![]() ,
,
то радиус сходимости
ряда![]() равен
этому пределу и степенной ряд сходится
при
,
т.е. в промежутке
равен
этому пределу и степенной ряд сходится
при
,
т.е. в промежутке
![]() ,
который называется промежутком
(интервалом) сходимости.
,
который называется промежутком
(интервалом) сходимости.
Если
![]() ,
то степенной ряд сходится в единственной
точке
,
то степенной ряд сходится в единственной
точке
![]() .
.
На концах промежутка ряд может сходиться (абсолютно или условно), но может и расходиться.
Сходимость
степенного ряда при
![]() и
и
![]() исследуется
с помощью какого-либо из признаков
сходимости.
исследуется
с помощью какого-либо из признаков
сходимости.
