
- •Раздел 1, Элементы общей теории сигналов.
- •Раздел 2. Преобразование Фурье.
- •2.1.2 Спектральное представления последовательности
- •2.1.2 Спектральное представления последовательности
- •Раздел 3. Корреляционный анализ.
- •Лекции по рцс.
- •Раздел 1, Элементы общей теории сигналов. Классификация сигналов
- •Ряд Фурье
- •Синусно-косинусная форма
- •Вещественная форма
- •Комплексная форма
- •Раздел 2. Преобразование Фурье. Примеры разложения сигналов в ряд Фурье
- •Последовательность прямоугольных импульсов
- •Пилообразный сигнал
- •Последовательность треугольных импульсов
- •Преобразование Фурье
- •Примеры расчета преобразования Фурье
- •Прямоугольный импульс
- •Несимметричный треугольный импульс
- •Симметричный треугольный импульс
- •Односторонний экспоненциальный импульс
- •Двусторонний экспоненциальный импульс
- •Гауссов импульс
- •Сигнал вида sin(X)/X
- •Свойства преобразования Фурье
- •Линейность
- •Задержка
- •Дифференцирование сигнала
- •Интегрирование сигнала
- •Спектр свертки сигналов
- •Спектр произведения сигналов
- •Умножение сигнала на гармоническую функцию
- •Связь преобразования Фурье и коэффициентов ряда Фурье
- •Фурье-анализ неинтегрируемых сигналов
- •Дельта-функция
- •Постоянный во времени сигнал (константа)
- •Функция единичного скачка
- •Гармонический сигнал
- •Раздел 3. Корреляционный анализ. Корреляционный анализ
- •Взаимная корреляционная функция
- •Связь между корреляционными функциями и спектрами сигналов
- •Энергетические расчеты в спектральной области
- •Комплексная огибающая
- •Преобразование Гильберта
- •Спектр аналитического сигнала
- •Случайные сигналы
- •Ансамбль реализаций
- •Модели случайных процессов
- •Гармонический сигнал со случайной начальной фазой
- •Вероятностные характеристики случайных процессов
- •Функциональные характеристики
- •Числовые характеристики
- •Корреляционные функции случайных процессов
- •Некоррелированность и статистическая независимость
- •Стационарные и эргодические случайные процессы
- •Стационарные случайные процессы
- •Эргодические случайные процессы
- •Спектральные характеристики случайных процессов
- •Случайный телеграфный сигнал
- •Вероятностные характеристики случайных процессов
Сигнал вида sin(X)/X
Следующий пример призван продемонстрировать дуальность преобразования Фурье. Если сравнить формулы прямого и обратного преобразования Фурье, можно заметить, что они отличаются друг от друга лишь знаком в показателе комплексной экспоненты и множителем перед интегралом. Отсюда следует, что если четной функции времени f(t) соответствует спектральная функция g(ω) (она будет также четной), то функции времени g(t) будет соответствовать спектральная функция 2πf(ω). Проверим это на конкретном примере. В начале этого раздела мы выяснили, что прямоугольному импульсу соответствует спектральная функция вида sin(ω)/ ω. Теперь же рассмотрим временной сигнал вида sin(t)/t и проверим, будет ли его спектральная функция прямоугольной. Итак, задаем временной сигнал (используем параметр Г для обозначения полупериода функции sin) (рис. 1.24):
![]()
Рассчитываем спектр и строим график (рис. 1.25):


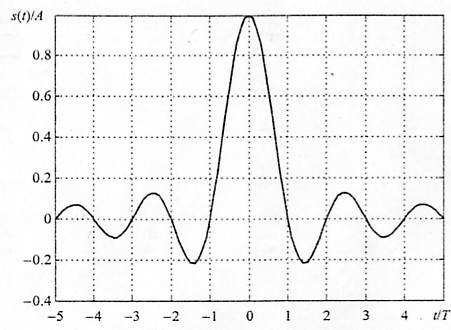
Рис. 1.24. Сигнал вида sin(at)/(at)

Рис. 1.25. Сигнал вида sin(at)/(at) имеет прямоугольный спектр
Значение каждого из двух получившихся интегралов равно ±п в зависимости от знака множителей (ω ± π/Т). Поэтому результат суммирования интегралов зависит от частоты следующим образом:

Как видите, дуальность (симметрия) преобразования Фурье получила наглядное подтверждение.
Сигнал данного вида имеет идеальный низкочастотный спектр — спектральная функция постоянна в некоторой полосе частот, начинающейся от нулевой частоты, и равна нулю за пределами этой полосы. Мы вновь встретимся с этим сигналом в главе 3 при обсуждении разложения сигналов в ряд Котельникова.
Свойства преобразования Фурье
Под свойствами преобразования Фурье подразумевается взаимное соответствие Трансформаций сигналов и их спектров. Хорошее знание свойств преобразования Фурье позволяет предсказывать примерный (а иногда и точный) вид спектра анализируемого сигнала и таким образом контролировать правдоподобность результата, выдаваемого компьютером.
В этом разделе мы будем рассматривать два абстрактных сигнала, f(t) и g(t), и считать, что их спектральные функции равны F(ω) и G(ω).
Линейность
Преобразование Фурье является линейным интегральным преобразованием. Смысл свойства линейности можно сформулировать так: спектр суммы равен сумме спектров. Говоря математическим языком, линейная комбинация сигналов имеет спектр в виде такой же (с темп же коэффициентами) линейной комбинации их спектральных функций:
если ![]() , то
, то ![]() .
.
Задержка
А теперь посмотрим, как сказывается на спектральной функции задержка сигнала во времени. Итак, пусть τ — время задержки:
![]() ,
,
тогда спектральная функция .изменится следующим образом:
![]()
Результат показывает, что спектр исходного сигнала оказался умноженным на
комплексную экспоненту вида e-jωτ. Таким образом, амплитудный спектр сигнала не меняется (ведь модуль такой комплексной экспоненты равен 1; к тому же здравый смысл подсказывает, что соотношение между амплитудами спектральных составляющих из-за сдвига сигнала во времени измениться не должно). Фазовый спектр приобретает дополнительное слагаемое -ωτ, линейно зависящее от частоты.
ЗАМЕЧАНИЕ
Если в результате какого-либо преобразования сигнала его спектр умножившем на некоторую функцию, не зависящую от преобразуемого сигнала, это означает, что данное преобразование может быть выполнено линейной системой с постоянными параметрами. Речь о системах данного класса пойдет в главе 2.
