
- •Раздел 1, Элементы общей теории сигналов.
- •Раздел 2. Преобразование Фурье.
- •2.1.2 Спектральное представления последовательности
- •2.1.2 Спектральное представления последовательности
- •Раздел 3. Корреляционный анализ.
- •Лекции по рцс.
- •Раздел 1, Элементы общей теории сигналов. Классификация сигналов
- •Ряд Фурье
- •Синусно-косинусная форма
- •Вещественная форма
- •Комплексная форма
- •Раздел 2. Преобразование Фурье. Примеры разложения сигналов в ряд Фурье
- •Последовательность прямоугольных импульсов
- •Пилообразный сигнал
- •Последовательность треугольных импульсов
- •Преобразование Фурье
- •Примеры расчета преобразования Фурье
- •Прямоугольный импульс
- •Несимметричный треугольный импульс
- •Симметричный треугольный импульс
- •Односторонний экспоненциальный импульс
- •Двусторонний экспоненциальный импульс
- •Гауссов импульс
- •Сигнал вида sin(X)/X
- •Свойства преобразования Фурье
- •Линейность
- •Задержка
- •Дифференцирование сигнала
- •Интегрирование сигнала
- •Спектр свертки сигналов
- •Спектр произведения сигналов
- •Умножение сигнала на гармоническую функцию
- •Связь преобразования Фурье и коэффициентов ряда Фурье
- •Фурье-анализ неинтегрируемых сигналов
- •Дельта-функция
- •Постоянный во времени сигнал (константа)
- •Функция единичного скачка
- •Гармонический сигнал
- •Раздел 3. Корреляционный анализ. Корреляционный анализ
- •Взаимная корреляционная функция
- •Связь между корреляционными функциями и спектрами сигналов
- •Энергетические расчеты в спектральной области
- •Комплексная огибающая
- •Преобразование Гильберта
- •Спектр аналитического сигнала
- •Случайные сигналы
- •Ансамбль реализаций
- •Модели случайных процессов
- •Гармонический сигнал со случайной начальной фазой
- •Вероятностные характеристики случайных процессов
- •Функциональные характеристики
- •Числовые характеристики
- •Корреляционные функции случайных процессов
- •Некоррелированность и статистическая независимость
- •Стационарные и эргодические случайные процессы
- •Стационарные случайные процессы
- •Эргодические случайные процессы
- •Спектральные характеристики случайных процессов
- •Случайный телеграфный сигнал
- •Вероятностные характеристики случайных процессов
Несимметричный треугольный импульс
Далее рассмотрим несимметричный треугольный импульс (рис. 1.14):


Рис. 1.14. Несимметричный треугольный импульс
Рассчитываем спектр и строим графики (рис. 1.15):
![]() .
.

Рис. 1.15. Амплитудный (слева) и фазовый (справа) спектры
несимметричного треугольного импульса
На сей раз амплитудный спектр не содержит ярко выраженных лепестков, поэтому для определения его эффективной ширины необходим иной критерий. Будем определять эффективную ширину спектра по уровню 0,1 от максимума. Из графика видно, что эта ширина (она показана стрелкой) составляет примерно 6π/Т. База сигнала, таким образом, равна 6π.
Симметричный треугольный импульс
Следующий сигнал — симметричный треугольный импульс (рис. 1.16):


Рис. 1.16. Симметричный треугольный импульс
Рассчитываем спектральную функцию:
![]()
Далее строим график амплитудного спектра (рис. 1.17). Спектральная функция оказывается не только вещественной (это сразу же следует из четности сигнала), но и неотрицательной, поэтому фазовый спектр в данном случае чисто нулевой и строить его график не имеет смысла.

Рис. 1.17. Амплитудный спектр симметричного треугольного импульса
Из графика видно, что спектр опять имеет лепестковую структуру и ширина главного лепестка составляет 2π/Т, как и в случае прямоугольного импульса. Однако длительность сигнала в данном случае вдвое больше (2T), и база оказывается равной 4π.
Далее перейдем от сигналов конечной длительности к бесконечно протяженным сигналам.
Односторонний экспоненциальный импульс
Первым из сигналов бесконечной длительности будет рассмотрен односторонний экспоненциальный импульс (рис. 1.18):
![]()
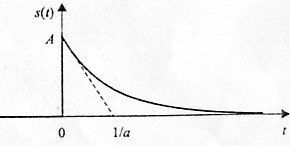
Рис. 1.18. Односторонний экспоненциальный импульс
Рассчитываем преобразование Фурье:
![]()
Далее строим графики амплитудного и фазового спектров (рис 1.19).

Рис. 1.19. Амплитудный (слева) и фазовый (справа) спектры
одностороннего экспоненциального импульса
Двусторонний экспоненциальный импульс
Теперь пусть экспоненциальный импульс будет двусторонним (симметричным, рис. 1.20):
![]()
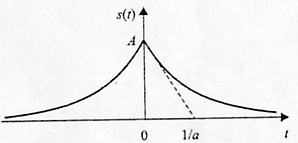
Рис. 1.20. Двусторонний экспоненциальный импульс

Рис. 1.21. Амплитудный спектр двустороннего экспоненциального импульса
Рассчитываем преобразование Фурье:
![]()
Спектр в данном случае чисто вещественный, поэтому строить график фазового
спектра нет смысла (рис. 1.21).
Гауссов импульс
Следующий очень важный сигнал — гауссов импульс (рис. 1.22). Как и предыдущий, он имеет бесконечную протяженность в обоих направлениях временной оси:
![]()

Рис. 1.22. Гауссов импульс
Вычисляем спектр:
![]()
Поскольку сигнал является четной функцией, его спектр чисто вещественный. Поэтому строим график только /1ля амплитудного спектра (рис. 1.23).
Важным свойством гауссова импульса является то, что его спектр тоже описывается гауссовой функцией.
Гауссов импульс имеет бесконечную протяженность как во временной, так и в частотной области. Определим его эффективную длительность и ширину спектра по уровню 1/е от максимума: τ=2/а, ∆ω=2а. База сигнала, таким образом, равна четырем.
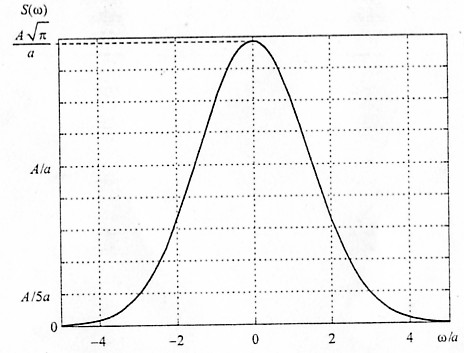
Рис. 1.23. Амплитудный спектр гауссова импульса
