Пилообразный сигнал

Следующий сигнал, который мы рассмотрим, — пилообразный (рис. 1.7). В пре­делах периода он описывается линейной функцией:

Данный сигнал является нечетной функцией, поэтому его ряд Фурье в синусно-косинусной форме (1.6) будет содержать только синусные слагаемые:

.

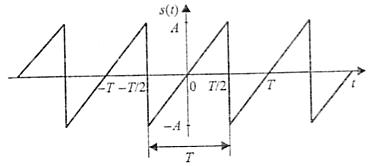
Рис. 1.7. Пилообразный сигнал

Сам ряд Фурье для пилообразного сигнала выглядит следующим образом:

У рассмотренных выше спектров прямоугольного и пилообразного периодиче­ских сигналов есть одна общая черта — амплитуды гармоник с ростом их номе­ров убывают пропорционально к. У следующего сигнала скорость затухания спектра будет иной, а почему, мы обсудим после расчета коэффициентов ряда Фурье для него.

Последовательность треугольных импульсов

Очередной сигнал, для которого мы получим разложение в ряд Фурье, представ­ляет собой периодическую последовательность треугольных импульсов. Строго говоря, импульсы в предыдущем сигнале тоже были треугольными, но в данном случае они будут иметь не пилообразную, а симметричную форму (рис. 1.8):

, .

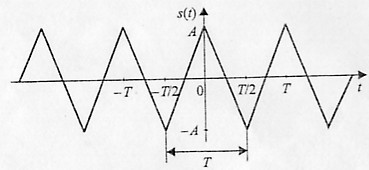
Рис. 1.8. Последовательность треугольных импульсов

Вычислим коэффициенты ряда Фурье (сигнал является четной функцией, по­этому в синусно-косинусной форме ряда Фурье (1.6) будут присутствовать толь­ко косинусные слагаемые):

.

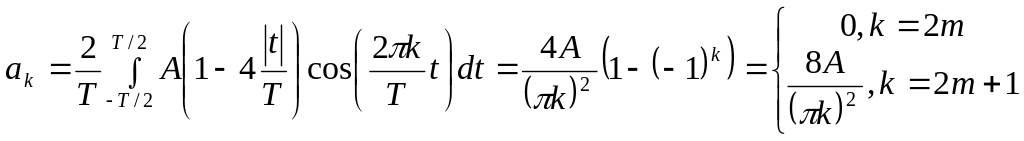Как и в случае меандра, здесь присутствует только нечетные гармоники. Сам ряд Фурье имеет следующий вид:

Как видите, в отличие от последовательностей прямоугольных и пилообразных импульсов, для треугольного периодического сигнала амплитуды гармоник убы­вают пропорционально второй степени номеров гармоник k. Это проявление об­щего правила, гласящего, что скорость убывания спектра зависит от степени гладкости сигнала. Прямоугольный и пилообразный сигналы имеют разрывы первого рода (скачки), и в их спектрах присутствует множитель 1/k. Треуголь­ный сигнал является непрерывной функцией (но ее первая производная содер­жит разрывы), и амплитуды гармоник его ряда Фурье содержат множитель 1/k² . Экстраполировав эту зависимость, получим следующее правило: если N — номер последней непрерывной производной сигнала, то спектр этого сигнала будет убывать со скоростью 1/k^N-2 , Предельным случаем является гармонический сиг­нал, дифференцировать который без потери непрерывности можно бесконечно. Согласно общему правилу, это даст бесконечную скорость убывания спектра, что вполне соответствует действительности (ряд Фурье для гармонического сиг­нала содержит только одну гармонику).

Преобразование Фурье

Преобразование Фурье (Fourier transform) является инструментом спектрально­го анализа непериодических сигналов. Впрочем, чуть позже мы увидим, что его можно применять и к сигналам периодическим, но это потребует использования аппарата обобщенных функций.

Для наглядной иллюстрации перехода от ряда Фурье к преобразованию Фурье часто используется не вполне строгий математически, но зато понятный подход. Представим себе периодическую последовательность импульсов произвольно­го вида и сформируем ряд Фурье для нее. Затем, не меняя формы одиночных импульсов, увеличим период их повторения (заполнив промежутки нулевым значением) и снова рассчитаем коэффициенты ряда Фурье. Формула (1.9) для расчета коэффициентов ряда показывает, что нам придется вычислить morn же самый интеграл, но для более тесно расположенных частот . Изменение пределов интегрирования не играет роли — ведь на добавившемся между им­пульсами пространстве сигнал имеет нулевое значение. Единственное дополни­тельное изменение будет состоять в уменьшении общего уровня гармоник из-за деления результата интегрирования на увеличившийся период Т.

На рис. 1.9 описанные изменения иллюстрируются на примере двукратного уве­личения периода следования прямоугольных импульсов. Обратите внимание на то, что горизонтальная ось спектральных графиков проградуирована в значени­ях частот, а не номеров гармоник.

Итак, с ростом периода следования импульсов гармоники располагаются ближе друг к другу по частоте, а общий уровень спектральных составляющих становит­ся все меньше. При этом вид вычисляемого интеграла (1.9) не меняется.

Наконец, если устремить период к бесконечности (превратив тем самым перио­дическую последовательность в одиночный импульс), гармоники спектра будут плотно занимать всю частотную ось, а их амплитуды упадут до нуля (станут бес­конечно малыми). Однако взаимное соотношение между уровнями гармоник ос­тается неизменным и определяется все тем же интегралом (1.9). Поэтому при спектральном анализе непериодических сигналов формула для расчета коэффи­циентов комплексного ряда Фурье модифицируется следующим образом:

• частота перестает быть дискретно меняющейся и становится непрерывным параметром преобразования (то есть 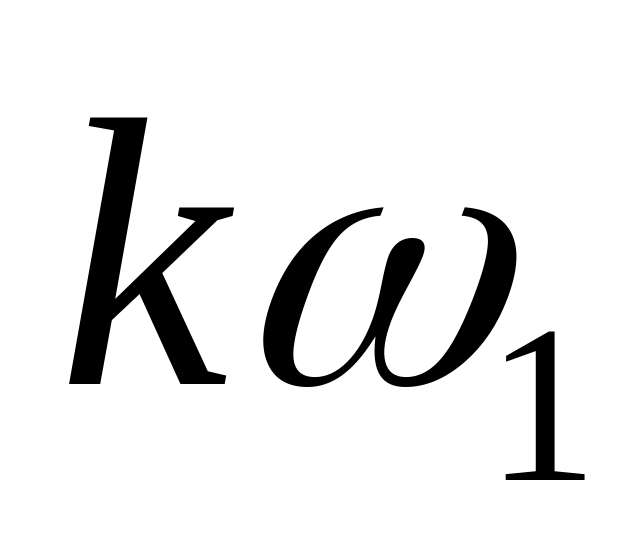в формуле (1.9) заменяется на ω);

• удаляется множитель 1/Т;

• результатом вычислений вместо нумерованных коэффициентов ряда Си явля­ется функция частоты S(ω) — спектральная функция сигнала s(t). Иногда ее называют также спектральной плотностью.

Рис. 1.9. Изменение спектра последовательности импульсов

при двукратном увеличении периода их следования

В результате перечисленных модификаций формула (1.9) превращается в фор­мулу прямого преобразования Фурье:

(1.11)

В формуле самого ряда Фурье суммирование, естественно, заменяется интегри­рованием (и, кроме того, перед интегралом появляется деление на 2π;). Получаю­щееся выражение называется обратным преобразованием Фурье:

. (1.12)

ЗАМЕЧАНИЕ

Если использовать не круговую частоту w, а обычную частоту/ = (о/(2я), формулы прямо­го и обратного преобразования Фурье становятся еще более симметричными, отличаясь лишь знаком в показателе экспоненты:

,

.

Чтобы преобразование Фурье было применимо, сигнал должен удовлетворять следующим требованиям:

• должны выполняться условия Дирихле (см. раздел «Ряд Фурье»);

• сигнал должен быть абсолютно интегрируемым. Это означает, что интеграл от его модуля должен быть конечной величиной:

.

Однако с привлечением математического аппарата обобщенных функций воз­можно выполнение Фурье-анализа и для некоторых сигналов, не удовлетворяю­щих этим требованиям (речь об этом пойдет далее, в разделе «Фурье-анализ неинтегрируемых сигналов»).

Если анализируемый сигнал s(t) — вещественная функция, то соответствующая спектральная функция S(ω) является «сопряженно-симметричной» относитель­но нулевой частоты. Это означает, что значения спектральной функции на часто­тах ω и -ω являются комплексно-сопряженными по отношению друг к другу:

.

Если s(t) — четная функция, то, как и в случае ряда Фурье, спектр будет чисто вещественным (и, следовательно, будет являться четной функцией). Если, на­против, s(t) — функция нечетная, то спектральная функция S(ω) будет чисто мнимой (и нечетной).

Модуль спектральной функции часто называют амплитудным спектром, а ее ар­гумент — фазовым спектром. Легко показать, что для вещественного сигнала ам­плитудный спектр является четной, а фазовый — нечетной функцией частоты:

,

.

Примеры расчета спектральных функции конкретных сигналов и соответствую­щие графики будут приведены далее.

Итак, преобразование Фурье (1.11) ставит в соответствие сигналу, заданному во времени, его спектральную функцию. При этом осуществляется переход из вре­менной области в частотную. Преобразование Фурье является взаимно-одно­значным, поэтому представление сигнала в частотной области (спектральная функция) содержит ровно столько же информации, сколько и исходный сигнал, заданный во временной области.