
- •Раздел 1, Элементы общей теории сигналов.
- •Раздел 2. Преобразование Фурье.
- •2.1.2 Спектральное представления последовательности
- •2.1.2 Спектральное представления последовательности
- •Раздел 3. Корреляционный анализ.
- •Лекции по рцс.
- •Раздел 1, Элементы общей теории сигналов. Классификация сигналов
- •Ряд Фурье
- •Синусно-косинусная форма
- •Вещественная форма
- •Комплексная форма
- •Раздел 2. Преобразование Фурье. Примеры разложения сигналов в ряд Фурье
- •Последовательность прямоугольных импульсов
- •Пилообразный сигнал
- •Последовательность треугольных импульсов
- •Преобразование Фурье
- •Примеры расчета преобразования Фурье
- •Прямоугольный импульс
- •Несимметричный треугольный импульс
- •Симметричный треугольный импульс
- •Односторонний экспоненциальный импульс
- •Двусторонний экспоненциальный импульс
- •Гауссов импульс
- •Сигнал вида sin(X)/X
- •Свойства преобразования Фурье
- •Линейность
- •Задержка
- •Дифференцирование сигнала
- •Интегрирование сигнала
- •Спектр свертки сигналов
- •Спектр произведения сигналов
- •Умножение сигнала на гармоническую функцию
- •Связь преобразования Фурье и коэффициентов ряда Фурье
- •Фурье-анализ неинтегрируемых сигналов
- •Дельта-функция
- •Постоянный во времени сигнал (константа)
- •Функция единичного скачка
- •Гармонический сигнал
- •Раздел 3. Корреляционный анализ. Корреляционный анализ
- •Взаимная корреляционная функция
- •Связь между корреляционными функциями и спектрами сигналов
- •Энергетические расчеты в спектральной области
- •Комплексная огибающая
- •Преобразование Гильберта
- •Спектр аналитического сигнала
- •Случайные сигналы
- •Ансамбль реализаций
- •Модели случайных процессов
- •Гармонический сигнал со случайной начальной фазой
- •Вероятностные характеристики случайных процессов
- •Функциональные характеристики
- •Числовые характеристики
- •Корреляционные функции случайных процессов
- •Некоррелированность и статистическая независимость
- •Стационарные и эргодические случайные процессы
- •Стационарные случайные процессы
- •Эргодические случайные процессы
- •Спектральные характеристики случайных процессов
- •Случайный телеграфный сигнал
- •Вероятностные характеристики случайных процессов
Преобразование Гильберта
Для выделения амплитуды п. фазы
произвольный сигнал s(t)
представляется как вещественная часть
комплексного сигнала
![]() (он называется аналитическим сигналом):
(он называется аналитическим сигналом):
![]() .
.
Вещественная часть аналитического
сигнала, естественно, должна совпадать
с исходным сигналом s(t).
Мнимая же часть
![]() называется сопряженным сигналим
пли квадратурным дополнением:
называется сопряженным сигналим
пли квадратурным дополнением:
![]()
Сопряженный сигнал получается из исходного с помощью преобразования Гиль-берта. Вычисляется преобразование Гильберта следующим образом:
![]() (1.26)
(1.26)
Данный интеграл представляет собой свертку сигнала s(t) и функции 1/(πt). Это означает, что преобразование Гильберта может быть выполнено линейной системой с постоянными параметрами (такие системы будут описаны в главе 2; забегая вперед, скажем, что система, осуществляющая преобразование Гильберта, является физически нереализуемой, поскольку ее импульсная характеристика имеет бесконечную протяженность в обоих направлениях временной оси). Из этого, в свою очередь, следует, что мы можем определить частотную характеристики преобразования Гильберта:
 (1.27)
(1.27)
Итак, АЧХ преобразования Гильберта равна единице всюду, кроме нулевой частоты, то есть преобразование Гильберта не меняет амплитудных соотношений в спектре сигнала, лишь удаляя из него постоянную составляющую. Фазы всех спектральных составляющих в области положительных частот уменьшаются на 90е. в области отрицательных частот — увеличиваются на 90°.
Таким образом, устройство, осуществляющее преобразование Гильберта, должно представлять собой идеальный фазовращатель, вносящий на всех частотах фазовый сдвиг, равный 90°.
Очевидно, что обратное преобразование Гильберта должно вносит!) такой же фазовый сдвиг, по с обратным знаком, опять же при сохранении амплитудных соотношений в спектре преобразуемого сигнала. Математически это будет выглядеть так:

Сравнение это]] формулы с коэффициентом передачи прямого преобразования
Гильберта (1.27) показывает, что
![]()
Следовательно, формулы обратного и прямого преобразований Гильберта различаются лишь знаком:
![]()
Спектр аналитического сигнала
Ранее уже было сказано, что аналитический сигнал получается путем добавления к вещественному сигналу s(t) мнимой части в виде его преобразования Гильберта:
![]()
Теперь вычислим спектр аналитического сигнала, учитывая, что преобразование Гильберта является линейным и его коэффициент передачи определяется формулой (1.27):

Полученный результат довольно любопытен. В области положительных частот спектры вещественного сигнала и добавленной мнимой части (с учетом дополнительного 90-градусного (разового сдвига, вносимого множителем j) складываются, давая удвоенный результат. В области же отрицательных частот эти спектры оказываются противофазными и взаимно уничтожаются. В результате спектр аналитического сигнала оказывается односторонним (рис. 1.28, а, 6). Итак, чтобы для произвольного сигнала определить амплитудную огибающую и фазовую функцию, необходимо прежде всего сформировать аналитический сигнал, получив его мнимую часть с помощью преобразования Гильберта. Далее амплитудная огибающая находится как модуль аналитического сигнала:
![]()
Полная фаза представляет собой аргумент комплексного аналитического сигнала:
![]()
Чтобы получить начальную фазу сигнала, нужно выделить из полной фазы линейное слагаемое ω0t. Для этого, в свою очередь, нужно знать значение нейтральной частоты ω0. После этого можно будет получить начальную фазу и комплексную огибающую:
![]()
![]()
Спектр комплексной огибающей представляет собой сдвинутый на ω0 спектр аналитического сигнала:
![]()
В общем случае спектр комплексной, огибающей не является симметричным относительно нулевой частоты (рис. 1.28, в).
Выбор центральной частоты ω0, вообще говоря, является произвольным. Для узкополосных сигналов существует «разумное» значение ω0, при использовании которого оказывается наиболее простой аналитическая запись комплексной огибающей. Например, для гармонического сигнала
![]()
аналитический сигнал имеет вид
![]()
Амплитудная огибающая равна А, полная фаза — Ω/ +φ. В общем случае, произвольное значение «средней» частоты ω0, мы получаем начальную фазу
![]()
и комплексную огибающую
![]()
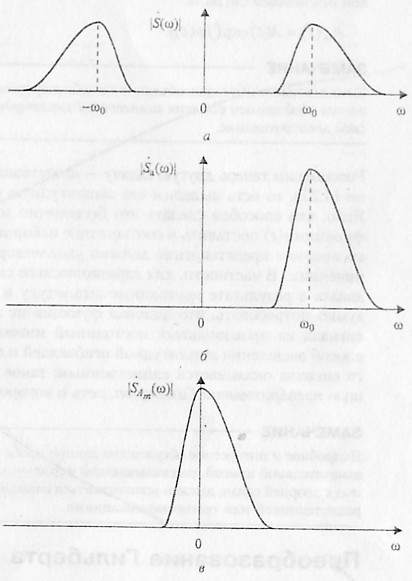
Рис. 1.28. Амплитудные спектры вещественного сигнала (а),
соответствующего ему аналитического сигнала (б) и его комплексной огибающей (в)
Если выбранная «средняя» частота ω0 будет совпадать с частотой гармонического сигнала (ω0 = Ω), комплексная огибающая станет константой:
![]()
Метод замены исходных функций их комплексными огибающими для анализа Прохождения сигналов через различные цепи называется методом низкочастотного эквивалента. При этом принципиально то, что все комплексные огибающие должны вычисляться относительно одной и той же центральной частоты ω0, далее если ее значение для некоторых сигналов будет выглядеть «неестественным».
В целом же следует помнить, что понятие комплексной огибающей имеет смысл только при указании частоты ω0 относительно которой эта комплексная огибающая вычислена.
