1.5. Решение задач [2]

1. В бочку заливается вода со скоростью 200 см³/с. На дне бочки образовалось отверстие площадью поперечного сечения 0,8 см. Пренебрегая вязкостью воды, определите уровень воды в бочке, /2/.

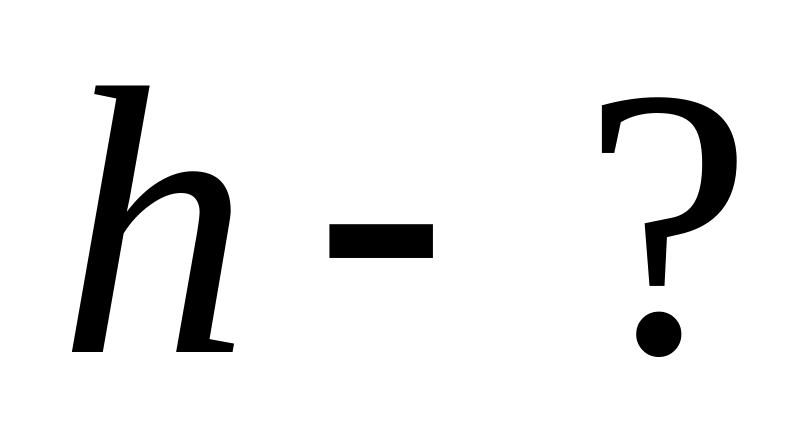2. Д ано: 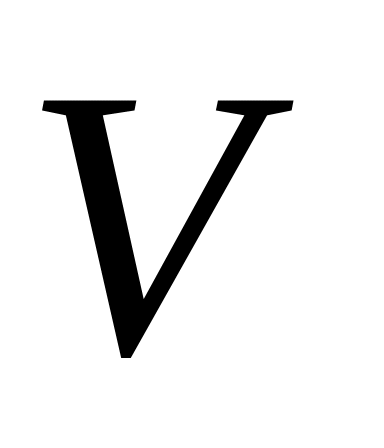=200 см³=2*10^-4 м³, 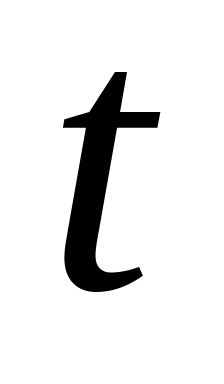=1 с,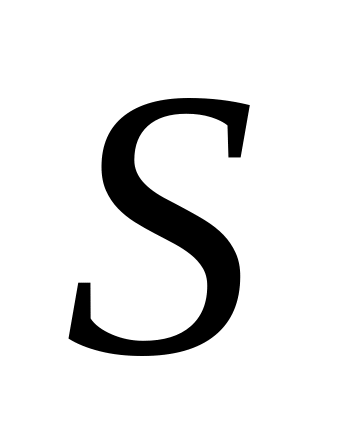 = 0,8 см²=8*10^-5 м².

Найти:

Решение:

Скорость истечения жидкости из малого отверстия (4) имеет вид:

, (6).

З десь: - ускорение свободного падения, - высота уровня воды в бочке над отверстием, которую можно выразить из выражения (6) в виде:

, (7).

Д ля определения величины , учтем, что . Отсюда

, (8).

Подставим в (8) исходные данные и получим

Ответ: .

3. По горизонтальной трубе в направлении, указанном на рисунке 8 стрелкой, течет жидкость. Размер уровней жидкости в манометрических трубках 1 и 2 одинакового диаметра составляет 8 см. Определите скорость течения жидкости по трубе, /2/.

Дано: = 8 см = 8*10^-2м, .

Найти: -?

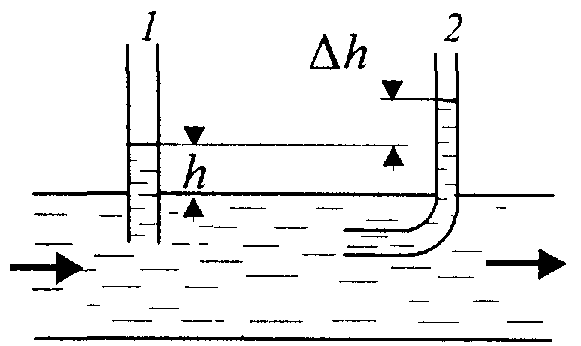
Рис. 8

Решение:

Гидростатическое давление столба жидкости в манометрических трубках уравновешивается давлением в соответствующем месте трубы, чем и определяется высота столба жидкости в этих трубках. В трубке 1 с горизонтальным срезом высота столба жидкости определяется только статическим давлением т.е. . Трубка Пито 2 имеет срез, позволяющий воде затекать в нее, поэтому высота столба жидкости в ней определяется суммой не только статического, но и динамического давления, . Следовательно, с одной стороны . С другой стороны .

Таким образом, ,

, (9).

В этих формулах - плотность жидкости, - ускорение свободного падения. Подставим в (9) исходные данные и получим

= 1,25 м/с.

Ответ: = 1,25 м/с.

4. Вдоль оси горизонтальной трубки диаметром 3 см, по которой течет углекислый газ, ( =7,5 кг/м³) установлена трубка Пито. Пренебрегая вязкостью, определите объем газа, проходящего за 1 секунду через сечение трубы, если разность уровней в жидкостном манометре составляет

=0,5 см. Плотность жидкости принять равной =1000 кг/м³ , /2/.

Дано: =7.5 кг/м³, =1000 кг/м³, d=3 см =3*10^-2 м, =0,5 см = 5*10^-2м,

t=1 c.

Найти:

Решение:

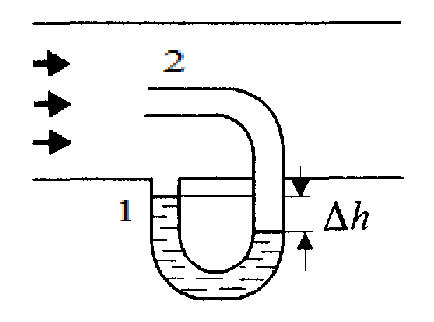
Рис. 9

Объем углекислого газа, протекающего за 1 секунду через сечение трубы выражается в виде: , (10).

Площадь поперечного сечения трубы равна . Разность уровней воды в трубке Пито обусловлена тем, что трубка 1 измеряет только статическое давление, а трубка 2 - сумму статического и динамического давления, следовательно , (рис. 9). С другой стороны , поэтому . Скорость течения углекислого газа по трубе выражается в виде . Подставим выражения для величин и в (10) и получим

, (11).

Рассчитаем искомую величину

=2,25*10^-3 м³.

Ответ: =2,25*10^-3 м³.

5. Пренебрегая вязкостью жидкости, определите скорость истечения жидкости из малого отверстия в стенке сосуда, если высота уровня жидкости над отверстием составляет 1,5м, /2/.

Дано: h=1,5м.

Найти: -?

Решение:

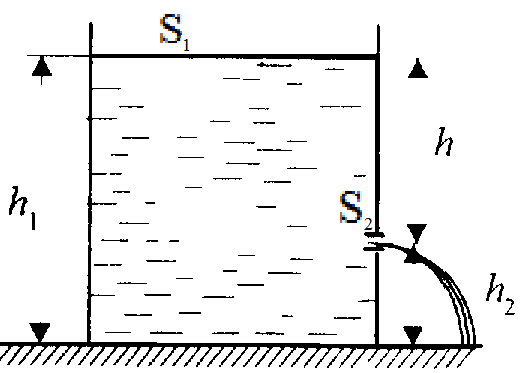Рис.10

Запишем уравнение Бернулли (12) и уравнение неразрывности (13) для трубки тока с сечениями S₁ и S₂ в виде

, (12),

, (13).

Так как (отверстие малое) из (13) следует, что и скоростью по сравнению со скоростью истечения жидкости из отверстия можно пренебречь. Следовательно и уравнение (12) приобретает вид . Отсюда скорость истечения жидкости из малого отверстия выражается в виде:

, (13).

Подставим в (13) числовые данные и получим

=5,42 м/с.

Ответ: =5,42 м/с.