МУ к практическим занятиям

1. Кинематика и динамика поступательного и вращательного движения. – Павлов

1.13, 1.14., 1.26, 1.39, 1.47, 1.153

2. Механические колебания и волны. – Мощенко

4.3, 4.25, 4.28, 4.118

3. Механика жидкости. – Ларина

1.214, 1.225, 1.229, 1.231

4. Молекулярная физика и термодинамика. – Снежков

2.7, 2.15, 2.30, 2.54, 2.58, 2.61

5. Электростатика и электромагнетизм. – Гольцов

3.10, 3.17, 3.75, 3.120, 3.143, 3.179

6. Геометрическая и волновая оптика. – Чебанова

5.7, 5.29, 5.45, 5.68, 5.88

7. Корпускулярные свойства света и тепловое излучение. – Чебанова

5.200, 5.212, 5.228, 5.178

8. Физика атома и атомного ядра. – Бугаян

6.5, 6.11, задачи 1, 2, 3 со стр. 351 (примеры решения задач)

МУ к практическим занятиям

1. Кинематика и динамика поступательного и вращательного движения. – Павлов

1.13, 1.14., 1.26, 1.39, 1.47, 1.153

2. Механические колебания и волны. – Мощенко

4.3, 4.25, 4.28, 4.118

3. Механика жидкости. – Ларина

1.214, 1.225, 1.229, 1.231

4. Молекулярная физика и термодинамика. – Снежков

2.7, 2.15, 2.30, 2.54, 2.58, 2.61

5. Электростатика и электромагнетизм. – Гольцов

3.10, 3.17, 3.75, 3.120, 3.143, 3.179

6. Геометрическая и волновая оптика. – Чебанова

5.7, 5.29, 5.45, 5.68, 5.88

7. Корпускулярные свойства света и тепловое излучение. – Чебанова

5.200, 5.212, 5.228, 5.178

8. Физика атома и атомного ядра. – Бугаян

6.5, 6.11, задачи 1, 2, 3 со стр. 351 (примеры решения задач)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено

на заседании кафедры физики

08 февраля 2012 г.

Методические указания

к практическим занятиям

«Механика жидкости»

Методические указания для всех специальностей и

для всех профилей всех направлений бакалавриата

очной и заочной форм обучения

Ростов-на-Дону

2012

УДК 531.383

Методические указания к практическим занятиям «Механика жидкости». – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 11 с.

Методические указания содержат краткую теорию по разделу «Механика жидкости», а также пояснения к решению серии задач данного раздела физики.

Предназначены для проведения практического занятия по теме «Механика жидкости» программы курса физики для студентов всех специальностей и всех профилей всех направлений бакалавриата очной и заочной форм обучения.

.

УДК 531.383

Составитель доц. Т.Н. Ларина

Рецензент доц. Ю.И. Гольцов

Редактор н.Е. Гладких

Темплан 2012 г., поз. ___

Подписано в печать ____). Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л 0,5. Тираж 100 экз. Заказ

Редакционно-издательский центр

Ростовского государственного строительного университета.

334022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2012

Краткая теория по теме «Динамика жидкостей»

1. Уравнение неразрывности [1]

Гидроаэромеханика использует единый подход к изучению жидкостей и газов, пренебрегающий сжимаемостью жидкости и газа и пользующийся единым понятием несжимаемой жидкости — жидкости, плотность которой всюду одинакова и не изменяется со временем.

Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 1).

Густота линии тока, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет

медленнее. Картина линий тока характеризует

направление и модуль скорости в разных точках

пространства.

Рис.1. Линии тока

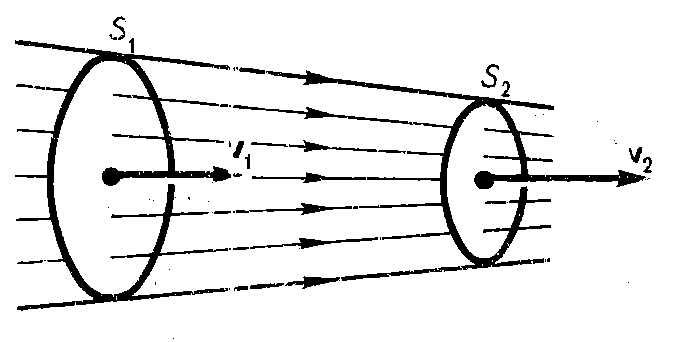Часть жидкости, ограниченную линиями тока,

называют трубкой тока. Течение жидкости

называется установившимся (или стационар-

ным), если форма и расположение линий тока, а

также значения скоростей в каждой ее точке со

Рис. 2. Трубка тока временем не изменяются. Рассмотрим какую-

либо трубку тока. Выберем два ее сечения и

, перпендикулярные направлению скорости (рис.2). Если жидкость несжимаема , то через сечение пройдет такой же объем жидкости, как и через сечение, т. е.

, (1) . Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока является величиной постоянной для данной трубки тока. Соотношение (1) называется уравнением неразрывности для несжимаемой жидкости.