Работа № 2 исследование структуры электромагнитного поля в резонаторах волноводного типа

Теоретическая часть

В диапазонах ультракоротких и более длинных волн в качестве колебательной системы обычно применяется контур, состоящий из ин­дуктивности , емкости и сопротивления потерь . Основными параметрами колебательных систем являются резонансная частота и добротность . С целью увеличения резонансной частоты контура приходится уменьшать его индуктивность, так как ми­нимальная величина емкости, как правило, ограничивается другими элементами устройства. В пределе катушка индуктивности вырождается в один виток, размеры которого имеют тот же порядок, что и длина волны, и контур интенсивно излучает электромагнитную энергию в ок­ружающее пространство. Вместе с тем увеличиваются и тепловые потери вследствие сильного поверхностного эффекта в проводниках. Все это приводит к тому, что добротность колебательного контура по мере укорочения резонансной длины волны уменьшается и уже на волнах де­циметрового диапазона становится недопустимо низкой.

Рис. 1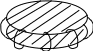

Дальнейший рост резонансной частоты может быть осуществлен пу­тем параллельного соединения витков , , …, , образующих результирующую индуктивность (рис. 1). При достаточно большом числе витков получится замкнутая поверхность, которая вместе с пластинами конденсатора полностью ограничит диэлектрический объем. В таких ко­лебательных системах, называемых резонаторами, потери энергии на излучение практически отсутствуют и, кроме того, значительно снижа­ются тепловые потери, т. к. проводники с током имеют весьма боль­шие поверхности. Вследствие этого резонаторы СВЧ обладают высокой добротностью.

Существует большое количество различных типов резонаторов, отличающихся друг от друга формой металлической поверхности.

Прямоугольный и цилиндрический резо­наторы представляют собой отрезки соответствующих волноводов, ограни­ченные с двух сторон плоскими прово­дящими стенками.

Задача о собственных колебаниях в резонаторах волноводного типа без потерь сводится к интегрирова­нию уравнений Максвелла:

;

в диэлектрическом объеме при граничных условиях . Из решения этой задачи следует, что в отсутствие вынуждающих источни­ков электромагнитное поле в идеальном резонаторе изменяется по гар­моническому закону с угловой частотой , называемой собственной частотой, а между векторами и имеется фазовый сдвиг, равный .

Рассмотрим происходящий в резонаторе волноводного типа процесс подробнее [3]. Пусть в волноводе с поперечным сечением произвольной формы вдоль оси распространяется бегущая волна, любая составляющая поля которой описывается уравнением

,

где  амплитуда произвольной составляющей поля, зависящая от поперечных координат и ;  круговая частота;  коэффициент распространения.

В результате отражения от поперечной стенки возникает отраженная волна, распространяющаяся в обратном направлении:

,

причем знак перед амплитудой волны зависит от граничных условий для составляющей поля на поперечной стенке.

Найдем сумму этих волн при условии, что они однотипны и их амплитуды одинаковы, т.е.

,

откуда находим два выражения для суммарного поля:

;

.

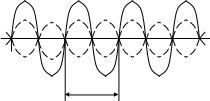
Это поле представляет собой в обоих случаях стоячую волну. На рис. 2 приведен график зависимости поля от координаты в разные моменты времени.

Картина поля не перемещается вдоль волновода. Меняется только значение поля во времени по гармоническому закону. Вдоль оси выделяются неподвижные точки, в которых поле равно нулю (уз- лы), и точки, в которых существует удвоенная амплитуда поля (пучности). При переходе через узел фаза поля меняется скачком на 180⁰, а в интервале между двумя соседними узлами фаза неизменна.

Рис. 2

Так как карти­на поля неподвижна и есть точки с нулевыми значениями поля, то пе­редача энергии вдоль волновода в стоячей волне отсутствует. Поэтому в случае стоячих волн в волноводе появляется принципиальная возможность установки поперечных стенок там, где равна нулю поперечная составляющая электрического поля и есть только поперечная составля­ющая магнитного поля. Очевидно, ^:что расстояние между этими стенками должно быть кратно половине длины волны в волноводе , при этом поле стоячей волны в волноводе не изменяется, т. к. выполне­ны все граничные условия, т.е.

, (1)

где =0, 1, 2,...

Поле в объемном резонаторе волноводного типа такое же, как и в волноводе со стоячей волной. Поэтому как в волноводе может сущест­вовать бесконечное число волн типа и , так и в резонаторе может существовать соответственно бесконечное количество колебаний типа и , каждое из которых имеет свою резонансную частоту.

Резонансные частоты и структура полей [1], [3]

Для определения резонансной частоты объемного резонатора используем условие резонанса (1), откуда длина волны в волноводе, со­ответствующая резонансу

. (2)

Длина волны в волноводе связана с длиной волны генератора следую­щим соотношением:

, (3)

где  критическая длина волны.

Из (3) находим

. (4)

Подставляя в (4) длину волны , соответствующую резонансу (2), получаем резонансную длину волны и частоту:

(5)

где ,  параметры заполнения резонатора.

Прямоугольные объемные резонаторы

В этом случае критическая длина волны определяется формулой

,

и формула резонансной длины волны приобретает вид

.

Резонансная длина волны и структура поля зависят от трех ин­дексов, поэтому различают колебания типа и ; это относится и к резонаторам на основе круглого волновода.

Из требования соответствия граничным условиям следует, что ко­лебания в резонаторе существуют, если нулю равен не более чем один индекс.

Картины полей колебаний в резонаторах соответствуют картинам полей стоячих волн в волноводах аналогичных типов. Основным типом колебаний прямоугольных резонаторов является колебание (рис. 3).

+

+ + +

+

Рис. 3

Цилиндрические объемные резонаторы

В этих резонаторах, как и в прямоугольных, существует беско­нечный ряд резонансных полей и частот, резонансная длина волны оп­ределяется соотношением (5), в котором для колебаний типа

, (6)

где  -й корень функции Бесселя -го порядка;  радиус основания резонатора.

Для волны типа

, (7)

где  -й корень первой производной функции Бесселя -го порядка.

Значения корней и для некоторых типов колебаний приве­дены в табл. 1 и 2.

Таблица l

Номер корня
	=0	=1	=2
1	2,405	3,832	5,135
2	5,52	7,016	8,417
3	8,654	10,173	11,650

Таблица 2

Номер корня
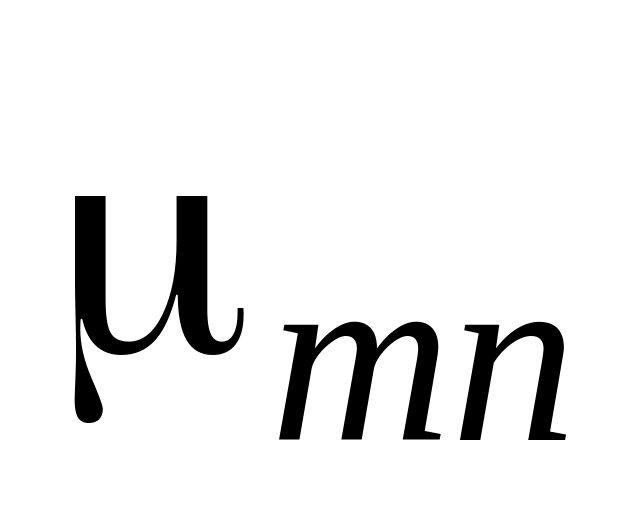
	=0	=1	=2
1	3,832	1,840	3,054
2	7,016	5,335	6,705
3	10,173	8,536	9,965

Колебания типа являются основными и соответствуют основной волне типа (рис. 4).

Колебания типа соответствуют волне типа (рис. 5).

Добротность резонаторов

Добротность  один из основных параметров объемного резонатора, характеризующий его резонансные свойства. Величина добротности определяется отношением энергии , запасенной в резонаторе, энергии , рассеиваемой за период колебаний , т.е.

.

Рис. 4

+ + + + +

. . . . .

Рис. 5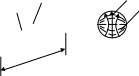

Рассеивание энергии происходит как в самом резонаторе, так и в связанных с ним внешних цепях. В связи с этим существует три различных понятия добротности:

 собственная (ненагруженная) добротность резонатора, учитывающая потери энергии только в самом резонаторе;

 внешняя добротность, учитывающая потери энергии во внешних цепях, связанных с резонатором;

 нагруженная добротность, учитывающая потери энергии как в самом резонаторе, так и во внешних цепях.

Значения собственной, внешней и нагруженной добротности связаны уравнением

.

Нагруженная добротность резонатора может в общем случае резко отличаться от собственной добротности . Величина одного и того же резонатора мажет изменяться в широких пределах за счет изменения связи с нагрузкой и возбуждающим генератором, который для резонатора также является нагрузкой. Очевидно, что при этом всегда выполняется неравенство < .

Расчет добротности по строгим уравнениям обычно затруднен из-за сложности определения потерь в стенках и органах механической настройки. Поэтому невысокая точность теоретических расчетов вели­чин делает особенно важным вопрос об ее экспериментальном определении.

Практически добротность резонаторов с двумя элементами связи, включенных по схеме четырехполюсника, обычно определяется по ширине резонансной кривой проходящей мощности. В основе метода измерения добротности резонаторов по ширине резонансной кривой лежит извест­ное соотношение

, (8)

где  резонансная частота;  полоса пропускания по уровню 0,5 от максимального пока­зания прибора.

Метод пробного тела

Исследование структуры поля объемного резонатора волноводного типа в данной лабораторной работе производится методом, основанным на изменении резонансной частоты резонатора под действием пробного тела.

Пусть резонатор 2 объема , заполненный воздухом с диэлектри­ческой проницаемостью и магнитной проницаемостью , возбуждает­ся от источника электромагнитных колебаний 1 (рис. 6) ( =1/120 Ф/м; =120 /с Гн/м; =310⁸ М/с).

Часть энергии из него отводится на детектор 3. Выпрямленный сигнал регистрируется измерительным прибором 4.

Собственная частота объемного резонатора  . На резонансной частоте запасенная в резонаторе максимальная энергия электрического поля равна максимальной энергии магнитного поля . Это энергетическое условие резонанса.

Генератор

1

Исследуемый резонатор

2

Детектор

3

Индикатор

4

Рис. 6

Если в резонатор ввести небольшое пробное диэлектрическое тело с параметрами > , = , то энергия электрического поля из­менится, т. к. диэлектрик запасает электрическую энергию.

Условие = теперь будет выполняться на некоторой другой частоте. Исследования показали, что изменение частоты про­порционально изменению запасенной электрической энергии:

,

где  коэффициент пропорциональности.

Запасенная диэлектриком энергия пропорциональна квадрату поля в точке, в которой находится пробное тело.

1

0,5

Рис. 7

Таким образом, перемещая по резонатору, в котором возбуждены колебания, пробное тело и измеряя , можно определить относитель­ную величину электрического поля.

Но непосредственное измерение величины затруднительно, поскольку пробное тело малых размеров приводит к малым изменениям . Поэтому можно поступить следующим образом.

Частотная характеристика резонатора (рис. 7) может быть описана зависимостью

,

где  показание измерительного прибора 7 (см. рис. 7) на частоте резонанса , когда пробное тело выведено; ,  полоса пропускания резонатора.

Если частоту генератора выбрать на середине линейного участка частотной характеристики невозмущенного резонатора, что соответствует показанию измерительного прибора , то введение пробного тела изменит частоту резонатора, а следовательно, и показания прибора на величину .

Относительная напряженность электрического поля

 .

Таким образом, используя тот факт, что изменения показаний индика­тора функционально связаны с изменением собственной частоты резона­тора, а следовательно, и с величиной напряженности электрического поля в месте нахождения пробного тела, можно снять картину распре­деления поля в резонаторе, перемещая пробные тела в заданных направлениях.

Более подробно метод пробного тела изложен в [2].

В данной лабораторной работе используются два пробных диэлект­рических ( > , = ) тела, одно из которых перемещается вдоль цилиндрического резонатора, а другое  по его диаметру.

Цель работы

1. Снятие резонансной характеристики и определение добротности резонатора.

2. Экспериментальное исследование распределения электричес­кого поля в цилиндрическом резонаторе.

3. Определение типа колебаний на базе экспериментальных данных.

Программа работы

В работе исследуются цилиндрический резонатор, его резонансные свойства и структура поля.

Размеры резонатора =9 см, =7,5 см. Способ возбуждения  петля связи, плоскость которой параллельна основанию цилиндра.

Расчетное задание (выполняется при подготовке)

1. Взять из приведенной ниже табл. 3 в соответствии с номером бригады два типа колебаний для цилиндрического и прямоугольного ре­зонаторов; принять =10 см.

Таблица 3

Тип и размеры резонатора	Номер бригады
	1	2	3	4	5	6
Цилиндрический =7,5 см
Прямоугольный =12 6 см2

2. Рассчитать:

а) величину критической длины волны ;

б) длину волны в волноводе , соответствующую заданному типу колебаний в резонаторе.

3. Найти длину резонатора 1 для этих типов колебаний.

4. Построить картины полей этих колебаний.

Порядок выполнения эксперимента

1. Снятие частотной характеристики и определение добротности резонатора (рис. 6):

а) включить приборы в сеть;

б) установить пробные тела в крайние положения;

в) найти резонансную частоту по максимуму показаний индикато­ра 4, перестраивая генератор 1;

г) записать значение резонансной частоты;

д) снять график зависимости показаний индикатора от частоты генератора;

е) построить частотную характеристику резонатора ;

ж) отметить на характеристике полосу пропускания резонатора;

з) вычислить добротность по формуле (8).

2. Определение структуры поля:

а) установить частоту генератора, соответствующую резонансной частоте исследуемого резонатора; зафиксировать показание индикатора;

б) ввести расстройку частоты генератора до значения, соответствующего положению рабочей точки ( );

в) снять зависимость показаний индикатора при перемещении пробного тела по диаметру;

г) снять зависимость показаний индикатора от положения пробного тела вдоль резонатора;

д) определить тип колебаний в резонаторе на основании полученных распределений поля (п. 2 в,г), используя соотношения (2)(7) (принять во внимание способ возбуждения).

Содержание отчета

1. Результаты выполнения расчетного задания.

2. Частотная характеристика.

3. Расчет добротности исследуемого резонатора.

4. Графики экспериментальных распределений в радиальном и продольном направлениях.

5. Определение типа колебания.

6. Построение структуры поля этого колебания.

7. Выводы.

Контрольные вопросы

1. Сформулировать условие резонанса в объемном резонаторе.

2. Назвать основные типы резонаторов.

3. Рассказать о добротности объемного резонатора.

4. Показать, как повлияет на добротность резонатора заполне­ние его диэлектриком без потерь при сохранении типа колебаний.

5. Назвать возможные типы колебаний в объемном резонаторе пря­моугольной и цилиндрической формы.

6. Объяснить смысл индексов , и в обозначении типа поля в резонаторе.

7. Показать, как изменится собственная резонансная частота прямоугольного резонатора с волной типа при изменении его дли­ны вдвое.

8. Рассказать о методе пробного тела для определения структуры поля в резонаторе,

9. Объяснить, почему на СВЧ невозможно применение контуров с сосредоточенными параметрами.

10. Назвать возможные области применения объемных резонаторов.

11. Показать, что в резонаторе без потерь нет переноса энергии в продольном направлении.

12. Пояснить принципиальную возможность объемных резонаторов (из уравнения баланса энергии электромагнитного поля).

13. Объяснить, почему резонаторы имеют множество резонансных частот.

14. Назвать способы возбуждения резонаторов.

15. Показать преимущества колебаний типа в круглом резо­наторе перед другими типами колебаний.

16. Рассказать о методике снятия частотной характеристики ре-зонатора.

17. Привести функциональную схему установки для измерения структуры поля методом пробного тела.

Библиографический список

1. Лебедев И. В. Техника и приборы СВЧ. Ч. 1. М.: Высшая школа, 1970. С. 342-349.

2. Гинзтон Э.Д. Измерения на сантиметровых волнах. М.: Иност­ранная литература, 1960. С. 534-552.

3. Ардабьевский А.И. Теория электромагнитного поля и распрост­ранения радиоволн. Ч.II. М.: МАИ, 1970. С. 136-146.