3. Характерні швидкості розподілу Максвела

Середня арифметична швидкість молекул v_сер. Використовуючи вираз для функції розподілу Максвела Fv, можна знайти значення середньої арифметичної швидкості молекул v_сер.

За означенням середня швидкість дорівнює відношенню суми швидкостей усіх молекул в одиниці об’єму до числа усіх молекул n у цьому об’ємі. Кількість молекул dn в одиниці об’єму, швидкості яких знаходяться в інтервалі (v, v+dv),

dn = n Fvdv

Тоді сума швидкостей усіх dn таких молекул дорівнюватиме:

vdn = v n F(v)dv

Але v змінюється від v = 0 до v = . Це означає, що сума швидкостей усіх молекул газу, які мають швидкості в інтервалі від v = 0 до v = , буде дорівнювати:

Нарешті, середня арифметична швидкість запишеться так:

(4)

Знайдемо значення середньої швидкості. Підставимо у вираз (4) замість F(v) її значення. Отримаємо:

(5)

Позначимо   .

Підставимо ці значення у вираз (5):

Проінтегрувавши вираз частинами, отримаємо одиницю. Таким чином, запишемо:

Вираз для знаходження середньої швидкості молекул газу:

. (6)

Середню квадратичну швидкість можна отримати з виразу:



Але для отримання даних формул можна використати і поняття функції розподілу:

.

Інтеграл у цій формулі знайдемо інтегруванням частинами:

,

звідси:

, . (7)

Як вже було відзначено раніше, функція розподілу Максвела F(v) приймає максимальне значення при деякому значенні vv_н, де v_н – найбільш ймовірна швидкість молекул.

Для її знаходження продиференцюємо F(v) за v² і похідну прирівняємо до нуля:

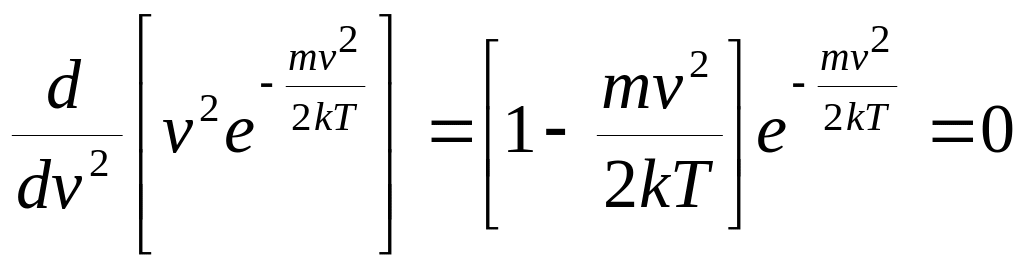
. (8)

П орівнюючи вирази (6), (7) і (8), отримаємо співвідношення між , і :

= 1,09 = 1,22

Оскільки ці швидкості відрізняються лише множником, то кожна з цих швидкостей може бути використана для характеристики теплового руху.

4. Експериментальна перевірка закону розподілу Максвела

Вперше експериментальна задачу про визначення швидкостей була вирішена в 1920 р. Отто Штерном, який вперше використав метод молекулярних пучків (м.п. - це вузькі потоки молекул, які літають у вакуумі без зіткнень прямолінійно). Але точність його методу була недостатньою.

В 1947 р. Штерн разом із Істерманом і Сімпсоном для перевірки закону розподілу закону молекул за швидкостями поставили інший більш складний і кропіткий дослід із використанням того ж методу молекулярних пучків. В цьому досліді спостерігались вільне падіння молекул пучка в полі сил тяжіння.

Д жерелом атомів являвся розплавлений цезій (температура його плавлення 301.1 К або 28.5 ^оС), який випаровувався із певної точки А. В ній цезій нагрівався до 450 К. З пічки атоми цезію вилітають через вузьку щілину шириною 0.02 мм . На відстані 1 мм від розташовується друга щілина такої ж ширини, як і перша. Мішень - тонкий вольфрамовий дріт товщиною 0.02 мм знаходиться на відстані 1 м від (дріт перпендикулярний до площині рисунка). Повний шлях пучку – 2 м. Весь пристрій розміщувався в посудині із високим вакуумом. Щілини , та мішень розташовувались на одній горизонтальній прямій.

Дріт-мішень нагрівають до такої температури, при якій атоми цезію, що попадають на неї, іонізуються і перетворюються на позитивні іони. Іони тут же лишають мішень і попадають на від’ємно заряджений циліндр, в якому власне дріт і розміщується (зрозуміло, що в ньому є прорізи для проходження атомів). Між дротом і циліндром тече струм, який після підсилення і вимірюється. Сила струму безпосередньо визначається кількістю іонів, а отже і кількістю атомів, що попали на дріт.

Атом цезію під дією сили тяжіння рухається за параболою. Отже навішень попадуть тільки частинки, що вилетіли під деяким кутом .

Для координат та будь-якої точки траєкторії можна записати

,

і - це рівняння параболи.

В точці траєкторії атомів , а рівняння параболи отримує вигляд

.

Звідси вираз для :

Тепер ми підставимо цю величину в рівняння параболи при x = L

.

Остаточно, зміщення атомів вздовж визначаються лише значенням , які при малих взагалі близькі до самої швидкості.

Якщо переміщувати дріт по висоті і вимірювати струм, то можна визначити кількість атомів, які мають різні швидкості. Тобто в такий спосіб можна переварити розподіл молекул за швидкостями.

Відзначимо, вимірявши кількість атомів на певній висоті, ми визначимо кількість атомів, які лежать у деякому інтервалі швидкостей, оскільки товщина дроту конечна і на неї попадають атоми з близькими, а не однаковими швидкостями.

В експерименті навіть найповільніші атоми зміщуються лише на 0.2 мм. Але ж товщина дроту складала 0.02 мм! Тобто вимірювання були проведені із достатньо великою точністю.

Вимірювання підтвердили розподіл Максвела.