Інтерполяція поліномами найменшого ухилення

У структурі виразу для оцінки похибки

(2.24)

перший множник головним чином залежить від поведінки функції в межах інтервалу інтерполювання. Другий множник - функція залежить суто від розташування вузлів. Розглянемо як поводить себе ця функція при рівномірній сітці вузлів і різній їх кількості.

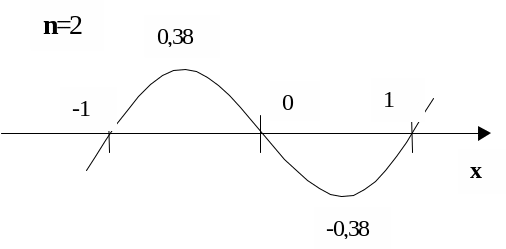
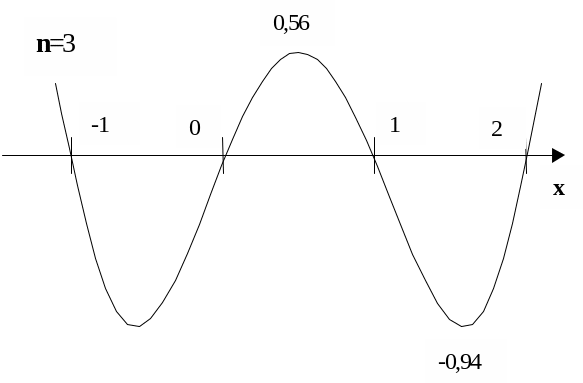
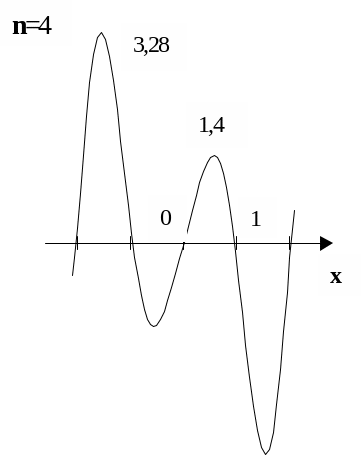
Як видно, зі збільшенням кількості вузлів, на яких визначається інтерполяційний поліном, тобто зі зростанням його степеня, зростають екстремальні значення функції . Це може привести до зростання похибки інтерполяції, якщо значення першого множника у (2.24) зі зростанням порядку не зменшується обернено пропорційно до .

З малюнку також видно, що найбільші значення знаходяться між ближніми до країв вузлами, а біля середини інтервалу інтерполювання вони значно менші. Це означає, що (при малому змінені похідної ) в межах інтервалу інтерполяції похибка зростає біля його кінців.

Мінімізувати максимальну можливу похибку можна за рахунок зміщення вузлів від центру до країв. При цьому можлива похибка у центрі зросте, а біля країв зменшиться. Оптимальний ефект буде досягнуто коли всі екстремальні значення будуть рівними. Інтерполяційні поліноми, які мають такі властивості, звуть поліномами найменшого ухилення. Щоб визначити відповідне до цього розташування вузлів, використовують поліноми Чебишова.

Поліноми Чебишова визначаються наступним чином:

. . при . (2.25)

Очевидно при =0 , при =1 .

Використовуючи відому тригонометричну формулу для косинуса суми:

,

при отримаємо:

,

що у свою чергу при порівнянні з (2.25) дає рекурентну формулу для визначення поліномів Чебишова:

. (2.26)

З використанням цієї формули та визначених вище поліномів і можна отримати поліноми Чебишова наступних степенів:

;

;

; . . . . . . .

З (2.25) очевидно, що ектремальні значення поліномів Чебишова при задовольняють умову:

. (2.27)

Це відповідає поведінці функції у випадку полінома найменшого ухилення. Тобто, для побудови інтерполяційного поліному найменшого ухилення на інтервалі , треба щоб вузли інтерполяції співпадали з нулями поліномів Чебишова відповідного степеня.

Нулі поліномів Чебишова є розв’язками рівняння

,

які визначаються наступною формулою:

, . (2.28)

Для довільного інтервалу інтерполяції вузлові значення аргументу можна отримати лінійним перетворенням значень за (2.28) з інтервалу на цей інтервал:

, .

Оцінка похибки при інтерполяція поліномами найменшого ухилення

Для вузлів за (2.28) на інтервалі :

.

Звідси, враховуючи (2.27),

.

Для інтервалу , тобто у рази більшого:

. (2.29)

Це дає оцінку для похибки аналогічно (2.14):

,

де як у (2.14) , .