
- •Введение
- •Глава 1 топологические пространства
- •1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества
- •2. Топология и топологическое пространство. База топологии
- •3. Структура открытых множеств и окрестности
- •4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств
- •5. Операция замыкания множества в топологическом пространстве
- •6. Внутренние точки множества, внутренность. Граница множества
- •7. Сепарабельные топологические пространства
- •8. Индуцированные топологии и фактортопология
- •9. Непрерывное отображение. Гомеоморфизм
- •10. Компактные пространства
- •Глава 2 свойства метрических пространств
- •1. Сходящиеся последовательности в метрических пространствах и полные метрические пространства
- •2. Теорема о пополнении метрического пространства
- •3. Критерий полноты пространства
- •4. Компактные множества в метрическом пространстве. Теорема Хаусдорфа
- •5. Критерии компактности в пространствах с[0, 1], lp. Теорема Арцела
- •6. Теорема Вейерштрасса о равномерном приближении и сепарабельность с[0, 1]
- •7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией
- •8. Принцип сжимающих отображений и его применение
- •9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра
- •Глава 3 мера и измеримые множества
- •1. Системы множеств
- •2. Системы множеств в евклидовом пространстве
- •3. Функция множеств
- •4. Мера и ее простейшие свойства. Мера в евклидовом пространстве
- •5. Внешняя мера
- •6. Измеримые множества
- •7. Мера Лебега на Rn
- •Глава 4 измеримые функции
- •1. Измеримые функции и их свойства
- •2. Сходимость почти всюду
- •3. Сходимость по мере и ее свойства
- •4. Сравнение сходимости почти всюду и по мере
- •5. Почти равномерная сходимость. Теоремы Егорова и Лузина
- •Глава 5 интеграл лебега
- •1. Интеграл Лебега для простых и ограниченных функций на пространстве с конечной мерой
- •2. Основные свойства интеграла от ограниченной функции
- •3. Определение интеграла Лебега в произвольном случае
- •4. Предельный переход под знаком интеграла
- •5. Сравнение интегралов Римана и Лебега
- •6. Заряды. Теорема Радона—Никодима
- •Глава 6 нормированные и гильбертовы пространства
- •2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности.
- •3. Скалярное произведение. Гильбертово пространство. Аксиомы и свойства. Ортонормированные системы. Ортогонализация по Шмидту. Тождество параллелограмма.
- •4. Ортогональность и ортогональное дополнение
- •5. Ряды Фурье в гильбертовом пространстве. Коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Полные и замкнутые ортонормированные системы
- •Глава 7 линейные операторы в нормированных пространствах
- •2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов
- •3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости
- •4. Ядро оператора. Критерий ограниченности обратного оператора. Теоремы об обратном операторе
- •5. Примеры обратных операторов. Обратимость операторов вида (I - a) и (a - c).
- •6. График оператора и замкнутые операторы. Критерий замкнутости. Теорема Банаха о замкнутом графике. Теорема об открытом отображении
- •Xn(t)X(t) равномерно на [a, b],.
- •X'n(t) y(t) равномерно на [а, b].
- •Глава 8 линейные функционалы в нормированных пространствах
- •1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха
- •2. Сопряженные пространства
- •3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций
- •4. Пространства Лебега и сопряженные к ним
- •5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера.
- •6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма.
- •Глава 9 спектральная теория операторов
- •1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта
- •2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора
- •3. Альтернативы Фредгольма. Теорема Шаудера о неподвижной точке.
- •Предметный указатель
2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора
Оказывается, АL(X, Y) и сопряженный к нему оператор A* L(Y*, X*) одновременно вполне непрерывны или нет. Точнее, имеет место следующая теорема Шаудера.
Теорема 3 (Шаудера). Пусть АL(X, Y), где Y – полное. Оператор А вполне непрерывен тогда и только тогда, когда А* вполне непрерывен.
Необходимость. Пусть S и S* – замкнутые единичные шары с центром в начале координат пространств X и Y* соответственно. Рассмотрим АK(X, Y). Возьмем произвольную последовательность функционалов {fn} S* и рассмотрим последовательность функций n (y) = fn(y), n=1, 2, ... На любом ограниченном в Y множестве эти функции равномерно ограничены (по n), так как |n (y)| = |fn(y)| ||fn||||y|| ||y|| и равностепенно непрерывны: |n (y1) - n (y2)| = |n (y1 - y2)| = |fn(y1 – y2)| ||fn||||y1 – y2||.
Будем рассматривать {n (y)} на множестве AS, которое компактно (ведь А вполне непрерывен) и замкнуто. По теореме Арцела найдется подпоследовательность {nk(Ax)} = {A*fnk(x)}, сходящаяся на S равномерно. Это означает, что {A*fnk} сходится в метрике X*. Следовательно, А* вполне непрерывен.
Достаточность. Пусть А* вполне непрерывен. Тогда по доказанному выше А** = (А*)* также вполне непрерывен. Пусть S** – замкнутый единичный шар в X**. Множество A**S** Y** относительно компактно. Так как пространство Y Y**, то в соответствии с этим вложением AS A**S** и, значит, AS относительно компактно в Y. Это и означает, что А вполне непрерывен. Теорема доказана.
Пусть А вполне непрерывный линейный оператор, действующий в банаховом пространстве X. Линейное уравнение вида (у Х)
х - Ах = у (3)
будем называть уравнением 2-го рода. Линейное уравнение Ах = у с вполне непрерывным оператором А будем называть уравнением 1-го рода. Как ни странно, теория линейных уравнений 2-го рода (3) намного проще по сравнению с теорией уравнений 1-го рода.
Перейдем к ее изложению. Наряду с уравнением (3) будем рассматривать соответствующее ему однородное уравнение
z – Az = 0, (4)
а также сопряженное уравнение
f – A*f = (3*)
и сопряженное однородное уравнение
f – A*f = 0 (4*)
Заметим, согласно теореме Шаудера оператор A* вполне непрерывен, так что все уравнения (3), (3*), (4), (4*) являются уравнениями 2-го рода. Докажем сначала следующее вспомогательное предложение.
Теорема 4. Пусть А – линейный вполне непрерывный оператор. Тогда множества значений операторов I – А и I – А* замкнуты и, значит, являются подпространствами в X и в X* соответственно.
Доказательство. Пусть {уn} принадлежит R(I – A) – множеству значений оператора I – А. Тогда найдутся xn X такие, что хn – Ахn = уn. Пусть уn у0 при n . Покажем, что y0 R(I – A). Рассмотрим ряд случаев. Если {хn} ограничена, то {Ахn} относительно компактна, откуда следует, что {хn} также относительно компактна. Достаточно заметить, что хn = уn + Ахn, где {yn} сходится, а {Ахn} относительно компактна. Вследствие компактности из {хn} можно выделить {хn(k)} – подпоследовательность, сходящуюся к х0; тогда, переходя к пределу при n(k) в равенстве хn(k) – Ахn(k) = уn(k) получим вследствие непрерывности А, что х0 – Ах0 = у0, т. е. у0 R (I – А).
Если {хn} не ограничена, то поступим следующим образом. Пусть N – подпространство нулей оператора I – A, т. е. множество всех решений уравнений (4). Введем расстояние dn = d(xn, N) = infz N ||xn – z||. Согласно определению нижней грани в N найдется элемент zn такой, что dn ||xn – zn|| (1 + 1/n)dn. Далее, (I – A) (хn – zn) = yn. Если {dn} ограничена, то, как и выше, с заменой хn на xn – zn получаем, что y0 R(I – A).
Оказывается, случай неограниченности {dn} невозможен. В самом деле, если {dn} не ограничена, то, переходя, если нужно, к подпоследовательности, можно считать, что dn , при n . Рассмотрим элементы
![]() .
.
Тогда
||un||
= 1 и (I – A)un
=
![]()
0, n
,
так как
0, n
,
так как
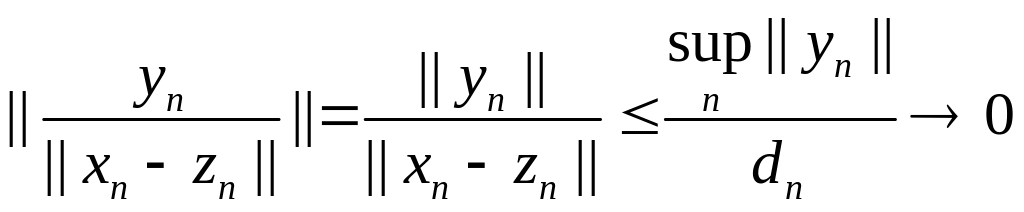 .
.
Как и выше, отсюда следует, что найдется подпоследовательность иn(k) u0, причем u0N. Но xn(k) – zn(k) – || xn(k) – zn(k)||u0 = (un(k) – u0) || xn(k) – zn(k)||. Причем zn(k) + || xn(k) – zn(k)||u0 N. Следовательно, по неравенству (3) имеем
||un(k) – u0||(1 + 1/nk)dn(k) || (un(k) – u0)||xn(k) – zn(k)|| || =
= ||xn(k) – {zn(k) + ||xn(k) – zn(k)||u0}|| dn(k)
откуда ||un(k) – u0|| n(k)/(n(k) + 1), а это противоречит тому, что ||un(k) – u0|| 0 при n(k) . Итак, {dn} ограничена и замкнутость R(I – A) доказана. Замкнутость R(I – A*) является следствием вышеизложенного, ибо А* также вполне непрерывен. Теорема доказана.
