
- •Введение
- •Глава 1 топологические пространства
- •1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества
- •2. Топология и топологическое пространство. База топологии
- •3. Структура открытых множеств и окрестности
- •4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств
- •5. Операция замыкания множества в топологическом пространстве
- •6. Внутренние точки множества, внутренность. Граница множества
- •7. Сепарабельные топологические пространства
- •8. Индуцированные топологии и фактортопология
- •9. Непрерывное отображение. Гомеоморфизм
- •10. Компактные пространства
- •Глава 2 свойства метрических пространств
- •1. Сходящиеся последовательности в метрических пространствах и полные метрические пространства
- •2. Теорема о пополнении метрического пространства
- •3. Критерий полноты пространства
- •4. Компактные множества в метрическом пространстве. Теорема Хаусдорфа
- •5. Критерии компактности в пространствах с[0, 1], lp. Теорема Арцела
- •6. Теорема Вейерштрасса о равномерном приближении и сепарабельность с[0, 1]
- •7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией
- •8. Принцип сжимающих отображений и его применение
- •9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра
- •Глава 3 мера и измеримые множества
- •1. Системы множеств
- •2. Системы множеств в евклидовом пространстве
- •3. Функция множеств
- •4. Мера и ее простейшие свойства. Мера в евклидовом пространстве
- •5. Внешняя мера
- •6. Измеримые множества
- •7. Мера Лебега на Rn
- •Глава 4 измеримые функции
- •1. Измеримые функции и их свойства
- •2. Сходимость почти всюду
- •3. Сходимость по мере и ее свойства
- •4. Сравнение сходимости почти всюду и по мере
- •5. Почти равномерная сходимость. Теоремы Егорова и Лузина
- •Глава 5 интеграл лебега
- •1. Интеграл Лебега для простых и ограниченных функций на пространстве с конечной мерой
- •2. Основные свойства интеграла от ограниченной функции
- •3. Определение интеграла Лебега в произвольном случае
- •4. Предельный переход под знаком интеграла
- •5. Сравнение интегралов Римана и Лебега
- •6. Заряды. Теорема Радона—Никодима
- •Глава 6 нормированные и гильбертовы пространства
- •2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности.
- •3. Скалярное произведение. Гильбертово пространство. Аксиомы и свойства. Ортонормированные системы. Ортогонализация по Шмидту. Тождество параллелограмма.
- •4. Ортогональность и ортогональное дополнение
- •5. Ряды Фурье в гильбертовом пространстве. Коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Полные и замкнутые ортонормированные системы
- •Глава 7 линейные операторы в нормированных пространствах
- •2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов
- •3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости
- •4. Ядро оператора. Критерий ограниченности обратного оператора. Теоремы об обратном операторе
- •5. Примеры обратных операторов. Обратимость операторов вида (I - a) и (a - c).
- •6. График оператора и замкнутые операторы. Критерий замкнутости. Теорема Банаха о замкнутом графике. Теорема об открытом отображении
- •Xn(t)X(t) равномерно на [a, b],.
- •X'n(t) y(t) равномерно на [а, b].
- •Глава 8 линейные функционалы в нормированных пространствах
- •1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха
- •2. Сопряженные пространства
- •3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций
- •4. Пространства Лебега и сопряженные к ним
- •5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера.
- •6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма.
- •Глава 9 спектральная теория операторов
- •1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта
- •2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора
- •3. Альтернативы Фредгольма. Теорема Шаудера о неподвижной точке.
- •Предметный указатель
2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности.
Пусть даны два линейных нормированных пространства Е1 и Е2. Мы будем называть эти пространства изоморфными, если существует взаимнонепрерывное (гомеоморфизм) биективное отображение Е1 на Е2. Имеет место следующая важная теорема:
Теорема 3. Все конечномерные линейные нормированные пространства данного числа измерений n изоморфны евклидову n-мерному пространству Rn и, следовательно, изоморфны друг другу.
Доказательство. Пусть Е есть n – мерное линейное нормированное пространство с нормой |||E|| и е1,…,еn - базис этого пространства. Тогда любой элемент однозначно представим в виде
x= ξ1e1+ …+ ξnen.
Поставим
элементу
![]() в соответствие элемент
в соответствие элемент
![]() =
(ξ1,
…,
ξn)
Rn
=
(ξ1,
…,
ξn)
Rn
Очевидно, что таким образом установленное соответствие между элементами x и является взаимно однозначным. Кроме того, это соответствие есть изоморфизм линейных пространств Е и Rn. Покажем, что оно взаимно непрерывно.
Для любого имеем
 (1)
(1)
В частности,
![]() ,
(2)
,
(2)
где β не зависит от x и y.
Установим теперь
неравенство противоположного знака.
На поверхности S
единичного
шара
![]() пространства Rn
(т.е. на компактном замкнутом множестве)
рассмотрим функцию
пространства Rn
(т.е. на компактном замкнутом множестве)
рассмотрим функцию
![]()
Так как на S все ξi не могут одновременно обращаться в нуль, то в силу линейной независимости е1,…,еn имеем
![]() .
.
Неравенство
![]()
показывает,
что
![]() - непрерывная функция. По теореме
Вейерштрасса эта функция достигает на
S своего
минимума α.
Легко видеть, что α>0.
Следовательно,
для
- непрерывная функция. По теореме
Вейерштрасса эта функция достигает на
S своего
минимума α.
Легко видеть, что α>0.
Следовательно,
для
![]()
![]()
откуда
для любого
![]() имеем
имеем
 (3)
(3)
Из (1) и (3) следует взаимная непрерывность отображения E на Rn. Теорема доказана.
Из гомеоморфизма E и Rn следует, что в конечномерном линейном нормированном пространстве сходимость по норме сводится к покоординатной сходимости и поэтому такое пространство всегда полное.
Для подпространства линейного нормированного пространства имеет место следующее важное предположение, установленное Ф. Риссом:
Теорема 4 (лемма Рисса о почти перпендикуляре). Пусть L – подпространство линейного нормированного пространства Е, несовпадающее с Е. Тогда для любого заданного ε > 0 найдётся в Е такой элемент y с нормой, равной единице, что
![]() для всех x
L.
для всех x
L.
Доказательство. Пусть y0 – любой элемент из Е, не принадлежащий L, и
![]()
Тогда d > 0, так как иначе y0 был бы предельным элементом для L и, следовательно, в силу замкнутости L, входил бы в L, что невозможно по условию. Далее
![]()
Положим
![]() .
.
Элемент
![]() (т.к. иначе
(т.к. иначе
![]() входил бы в L)
и
входил бы в L)
и
![]() Возьмём любой элемент
Возьмём любой элемент
![]() .
Пусть
.
Пусть
![]() ,
L.
Тогда
,
L.
Тогда
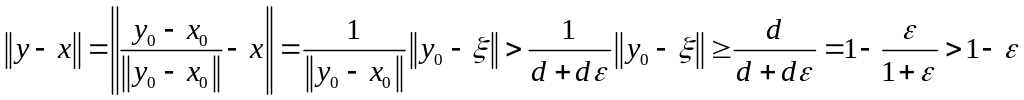 ,
,
что и требовалось доказать.
Известно, что в n-мерном евклидовом пространстве всякое ограниченное множество компактно. Докажем, что компактность ограниченных множеств, есть характеристическое свойство конечномерных линейных нормированных пространств.
Теорема 5 (теорема Рисса о локальной компактности). Для того, чтобы подпространство L линейного нормированного подпространства Е было конечномерным, необходимо и достаточно, чтобы каждое ограниченное множество элементов из L было относительно компактно.
Необходимость.
Пусть L n-мерно. Тогда L гомеоморфно
n-мерному евклидову пространству Rn.
Ограниченное множество
![]() взаимно
однозначно и взаимно непрерывно
преобразуется в ограниченное множество
N
Rn,
и так как N в Rn
относительно компактно, то M в L также
относительно компактно.
взаимно
однозначно и взаимно непрерывно
преобразуется в ограниченное множество
N
Rn,
и так как N в Rn
относительно компактно, то M в L также
относительно компактно.
Достаточность.
Предположим,
что каждое ограниченное множество
элементов из L относительно компактно.
Возьмем в L произвольный элемент x1,
![]() .
Обозначим через
.
Обозначим через
![]() подпространство, порожденное элементом
подпространство, порожденное элементом
![]() .
Если L =
,
то теорема доказана. Если же
не совпадает с L, то по теореме 3. найдется
в L элемент
.
Если L =
,
то теорема доказана. Если же
не совпадает с L, то по теореме 3. найдется
в L элемент
![]() такой, что
такой, что
![]() и
и
![]() .
Обозначим через
.
Обозначим через
![]() подпространство, порождаемое элементами
и
.
Имеются 2 возможности: либо L =
и теорема доказана, либо
не совпадает с L. Тогда по той же теореме
найдется элемент
подпространство, порождаемое элементами
и
.
Имеются 2 возможности: либо L =
и теорема доказана, либо
не совпадает с L. Тогда по той же теореме
найдется элемент
![]() такой, что
такой, что
![]() и
и
![]() .
Продолжим этот процесс. Тогда можно
сделать 2 предположения: либо для
некоторого n подпространство
.
Продолжим этот процесс. Тогда можно
сделать 2 предположения: либо для
некоторого n подпространство
![]() совпадет
с L и теорема будет доказана, либо мы
построим бесконечную последовательность
совпадет
с L и теорема будет доказана, либо мы
построим бесконечную последовательность
![]() такую, что
такую, что
![]() и
и
![]() при
при
![]() для
любых n
и m,.
Но вторая возможность отпадает, т.к. она
означала бы существование ограниченного
(
)
множества
для
любых n
и m,.
Но вторая возможность отпадает, т.к. она
означала бы существование ограниченного
(
)
множества
![]() ,
из которого нельзя выделить фундаментальную
подпоследовательность (
,
из которого нельзя выделить фундаментальную
подпоследовательность (![]() ),
что противоречит условию теоремы.
),
что противоречит условию теоремы.
