
- •Введение
- •Глава 1 топологические пространства
- •1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества
- •2. Топология и топологическое пространство. База топологии
- •3. Структура открытых множеств и окрестности
- •4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств
- •5. Операция замыкания множества в топологическом пространстве
- •6. Внутренние точки множества, внутренность. Граница множества
- •7. Сепарабельные топологические пространства
- •8. Индуцированные топологии и фактортопология
- •9. Непрерывное отображение. Гомеоморфизм
- •10. Компактные пространства
- •Глава 2 свойства метрических пространств
- •1. Сходящиеся последовательности в метрических пространствах и полные метрические пространства
- •2. Теорема о пополнении метрического пространства
- •3. Критерий полноты пространства
- •4. Компактные множества в метрическом пространстве. Теорема Хаусдорфа
- •5. Критерии компактности в пространствах с[0, 1], lp. Теорема Арцела
- •6. Теорема Вейерштрасса о равномерном приближении и сепарабельность с[0, 1]
- •7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией
- •8. Принцип сжимающих отображений и его применение
- •9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра
- •Глава 3 мера и измеримые множества
- •1. Системы множеств
- •2. Системы множеств в евклидовом пространстве
- •3. Функция множеств
- •4. Мера и ее простейшие свойства. Мера в евклидовом пространстве
- •5. Внешняя мера
- •6. Измеримые множества
- •7. Мера Лебега на Rn
- •Глава 4 измеримые функции
- •1. Измеримые функции и их свойства
- •2. Сходимость почти всюду
- •3. Сходимость по мере и ее свойства
- •4. Сравнение сходимости почти всюду и по мере
- •5. Почти равномерная сходимость. Теоремы Егорова и Лузина
- •Глава 5 интеграл лебега
- •1. Интеграл Лебега для простых и ограниченных функций на пространстве с конечной мерой
- •2. Основные свойства интеграла от ограниченной функции
- •3. Определение интеграла Лебега в произвольном случае
- •4. Предельный переход под знаком интеграла
- •5. Сравнение интегралов Римана и Лебега
- •6. Заряды. Теорема Радона—Никодима
- •Глава 6 нормированные и гильбертовы пространства
- •2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности.
- •3. Скалярное произведение. Гильбертово пространство. Аксиомы и свойства. Ортонормированные системы. Ортогонализация по Шмидту. Тождество параллелограмма.
- •4. Ортогональность и ортогональное дополнение
- •5. Ряды Фурье в гильбертовом пространстве. Коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Полные и замкнутые ортонормированные системы
- •Глава 7 линейные операторы в нормированных пространствах
- •2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов
- •3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости
- •4. Ядро оператора. Критерий ограниченности обратного оператора. Теоремы об обратном операторе
- •5. Примеры обратных операторов. Обратимость операторов вида (I - a) и (a - c).
- •6. График оператора и замкнутые операторы. Критерий замкнутости. Теорема Банаха о замкнутом графике. Теорема об открытом отображении
- •Xn(t)X(t) равномерно на [a, b],.
- •X'n(t) y(t) равномерно на [а, b].
- •Глава 8 линейные функционалы в нормированных пространствах
- •1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха
- •2. Сопряженные пространства
- •3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций
- •4. Пространства Лебега и сопряженные к ним
- •5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера.
- •6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма.
- •Глава 9 спектральная теория операторов
- •1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта
- •2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора
- •3. Альтернативы Фредгольма. Теорема Шаудера о неподвижной точке.
- •Предметный указатель
3. Функция множеств
Определение 14. Вещественнозначная функция, областью определения которой является некоторая система множеств , называется функцией множества.
Определение
15. Функция
f
называется счетно-аддитивной,
если для любой не более чем счетной
совокупности дизъюнктных множеств An
,
объединение которых А =
![]() An
тоже принадлежит ,
имеет место равенство
An
тоже принадлежит ,
имеет место равенство
![]()
Определение 16. Если равенство ограничено случаем, когда А есть объединение конечного числа дизъюнктных множеств Аn (А, Аn ), то функция f называется конечно-аддитивной или просто аддитивной.
Так как функции могут принимать бесконечные значения необходимо договориться об арифметических операциях над символами бесконечность. В основном эти правила аналогичные тем, которые применялись в математическом анализе. Например: а = ; + = и т.п. Но есть определенные отличия. Так мы полагаем, что 0 = 0 и - = - - (-) = 0. В математическом анализе последние два действия полагались неопределенностью.
Лемма 2. Если функция множеств f является аддитивной, принимает конечные значения на множествах А, В, В\А и А В, то f(B\A) = f(B) – f(A).
Утверждение легко вытекает из дизъюнктного представления В = А + В\А.
Следствие. Если функция множеств f является аддитивной, неотрицательной, принимает конечные значения на множествах А, В, В\А и А В, то f(B) f(A).
Теорема 4. Для того, чтобы аддитивная функция f, принимающая конечные значения и заданная на кольце , была счетно-аддитивной, необходимо и достаточно, чтобы для любой убывающей последовательности множеств Аi (i = 1,2,...), т.е. таких что А1 А2 А3 …, с пустым пересечением выполнялось f(Ai) 0 при i .
Необходимость.
Пусть Аi
убывающая последовательность множеств,
т.е., при этом
![]() = .
Построим систему непересекающихся
множеств Bi
= Ai\Ai+1.
Тогда нетрудно видеть, что А1
=
= .
Построим систему непересекающихся
множеств Bi
= Ai\Ai+1.
Тогда нетрудно видеть, что А1
=
![]() .
В силу счетной аддитивности функции
множеств f(A1)
=
.
В силу счетной аддитивности функции
множеств f(A1)
=
![]() .
Последнее равенство означает, что
.
Последнее равенство означает, что
![]() при n
.
Но
при n
.
Но
![]() .
Последнее равенство в сочетание с
поведением частичных сумм доказывает
утверждение.
.
Последнее равенство в сочетание с
поведением частичных сумм доказывает
утверждение.
Достаточность.
Пусть
дизъюнктные
множества An
,
объединение которых А =
![]() Ak
тоже принадлежит .
Построим последовательность убывающих
множеств Вn
= A\
Ak
тоже принадлежит .
Построим последовательность убывающих
множеств Вn
= A\
![]() .
В силу леммы, аддитивности функции
множества и условий теоремы f(Bn)
= f(A)
– f(
)
= f(A)
-
.
В силу леммы, аддитивности функции
множества и условий теоремы f(Bn)
= f(A)
– f(
)
= f(A)
-
![]()
0. Последнее доказывает счетную
аддитивность функции множеств.
0. Последнее доказывает счетную
аддитивность функции множеств.
Следующая теорема доказывается аналогично.
Теорема 5. Пусть f - счетно-аддитивная функция, заданная на кольце . Если А и А = Аi, где Ai и образуют возрастающую последовательность, т.е. А1 А2 …, то
f(A)
=
![]() f(Ai).
f(Ai).
То же
равенство справедливо, если А =
![]() Аi
(А, Аi
),
Аi
образуют убывающую последовательность
и f(Ai)
конечные числа, начиная с некоторого
i.
Аi
(А, Аi
),
Аi
образуют убывающую последовательность
и f(Ai)
конечные числа, начиная с некоторого
i.
4. Мера и ее простейшие свойства. Мера в евклидовом пространстве
Определение 17. Пусть X - любое множество. Мерой в X называется вещественнозначная неотрицательная счетно-аддитивная функция m, заданная на некотором полукольце подмножеств множества X.
Определение 18. Мера m называется конечной, если m(А) < + для А .
Определение
19. Мера
m
называется -конечной,
если
А
такие Аn
(n
=
1, 2,...),
что А
![]() и мера m(Аn)
< +
для
n.
и мера m(Аn)
< +
для
n.
Определение 20. Пусть m – произвольная мера в X, заданная на каком-то полукольце . Она называется полной, если из того, что А , m(А) = 0 и Е А вытекает, что Е .
Лемма
3.
Если
- полукольцо, An
,
A
=
,
то
=
![]() ,
где Сk
,
при этом для каждого k
существует n(k)
такое, что Сk
An(k).
,
где Сk
,
при этом для каждого k
существует n(k)
такое, что Сk
An(k).
Доказательство. Очевидно, что
А = А1[(А\А1)A2][(A\A1)(A\A2)A3]…[ (A\Ak)An+1]… (1)
Заметим,
сразу, что все множества, стоящие в
квадратных скобках дизъюнктны между
собой по построению. По условиям
полукольца А\Аk
=
![]() ,
где Сki
.
Следовательно
,
где Сki
.
Следовательно
(A\Ak)An+1
=
![]() An+1
=
An+1
=
=
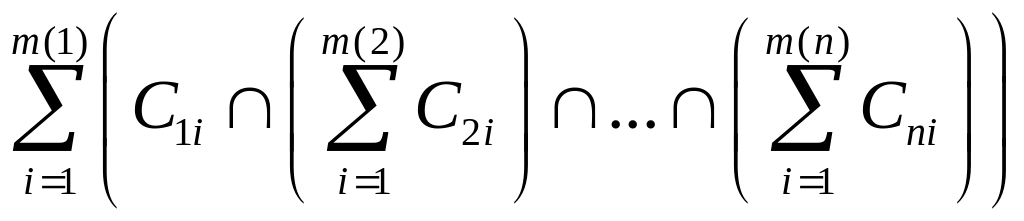 An+1
=
An+1
=
 An+1
=
An+1
=
=
![]() .
.
Стоящие в последних скобках множества по определению полукольца принадлежат ему и все между собой дизъюнктны. Подставив полученное равенство в (1) получим доказываемое.
Теорема 6. Пусть X – любое множество с полукольцом и неотрицательной конечно-аддитивной функцией множеств m на этом полукольце. Справедливы следующие свойства:
1. m() = 0;
2. Если А, В и А В, то m(A) m(B) (монотонность меры);
Если m является мерой (т.е. обладает еще свойством счетной аддитивности), то
3.
Если А, An
и А
,
то m(A)
![]() (полуаддитивность
меры)
(полуаддитивность
меры)
Доказательство. 1) Легко вытекает из свойства аддитивности и неотрицательности, так как m() = m() = m() + m() = 2m().
2)
В силу свойств полукольца найдется
конечный набор множеств Сk
таких, что В = А +
![]() Сk.Тогда
из аддитивности m
вытекает m(B)
= m(A)
+
m(Сk),
откуда и неотрицательности m
уже легко следует нужное неравенство.
Сk.Тогда
из аддитивности m
вытекает m(B)
= m(A)
+
m(Сk),
откуда и неотрицательности m
уже легко следует нужное неравенство.
3)
Из условий теоремы получаем представление
А =
![]() ,
где Вn
=
AAn.
Воспользуемся теперь леммой: А =
,
где Сk.
Отметим, что в силу леммы
,
где Вn
=
AAn.
Воспользуемся теперь леммой: А =
,
где Сk.
Отметим, что в силу леммы
![]() ,
,
при этом одно и тоже Сk может полностью попасть в разные Аn (но, что очень важно в силу леммы, хотя бы в одно из них обязательно попадает полностью). Отсюда уже легко следует, что
m(А)
=
![]() .
.
Теорема 7. Функция V, заданная на полукольце ячеек в Rn и равная для каждой ячейки ее объему – -конечная мера в Rn.
Доказательство. Практически в доказательстве нуждается только счетная аддитивность введенной функции, так как конечная аддитивность очевидна. Пусть {a1, b1;...; аn, bn} = {c1(k), d1(k);…; cn(k), dn(k)}. Далее предполагаем, что все ячейки, входящие в сумму имеют конечные ребра, в противном случае равенство очевидно. Ясно, что {c1(k), d1(k);…; cn(k), dn(k)} {a1, b1;...; аn, bn} для любого m. В силу монотонности и аддитивности функции множеств V выполняется неравенство V( {c1(k), d1(k);…; cn(k), dn(k)}) = V({c1(k), d1(k);…; cn(k), dn(k)}) V( {a1, b1;...; аn, bn}) для любого m. Предельным переходом по m получаем неравенство
V({c1(k), d1(k);…; cn(k), dn(k)}) V( {a1, b1;...; аn, bn}).
Докажем противоположное неравенство. Рассмотрим систему открытых параллелепипедов {0{c1(k) - /2k, d1(k) + /2k; …..; cn(k) - /2k, dn(k) + /2k}}, где произвольное положительное число. Данная система покрывает замкнутый параллелепипед *{a1, b1;...; аn, bn}. Так как последний является компактным множеством (он ограничен и замкнут), то из этого покрытия можно выделить конечное подпокрытие:
*{a1,
b1;...;
аn,
bn}
![]() 0{c1(k)
- /2k,
d1(k)
+ /2k;
…..; cn(k)
- /2k,
dn(k)
+ /2k}
0{c1(k)
- /2k,
d1(k)
+ /2k;
…..; cn(k)
- /2k,
dn(k)
+ /2k}
(без ограничения общности мы предположили, что нужное конечное покрытие находится в начале). Тогда
V(*{a1, b1;...; аn, bn})
V( 0{c1(k) - /2k, d1(k) + /2k; …..; cn(k) - /2k, dn(k) + /2k})
V(0{c1(k) - /2k, d1(k) + /2k; …..; cn(k) - /2k, dn(k) + /2k})
V(0{c1(k) - /2k, d1(k) + /2k; …..; cn(k) - /2k, dn(k) + /2k})
V(0{c1(k), d1(k); …..; cn(k), dn(k)}) + 2nV(*{a1, b1;...; аn, bn}) /2k =
= V(0{c1(k), d1(k); …..; cn(k), dn(k)}) + 2nV(*{a1, b1;...; аn, bn}).
В силу произвольности последнее доказывает противоположное неравенство.
