3.1.2. Пример расчета статически определимого бруса при растяжении-сжатии

На стальной ступенчатый брус круглого сечения, схема которого представлена на рис.7, действует система сил.

Т

Рис.7.

ребуется построить эпюры продольных сил, подобрать поперечные сечения всех участков бруса, определить нормальные напряжения и осевые перемещения.

Принято допускаемое напряжение на растяжение для стали: МПа.

Решение:

1. Разобьём брус на участки. Границы участков определяются сечениями, где изменяются поперечные размеры и приложены внешние нагрузки (рис.7).

2. Для определения продольных сил воспользуемся методом сечений (РОЗУ). Мысленно рассечём брус в пределах участка 1 и отбросим левую часть бруса. Для уравновешивания силы F₁ необходимо, чтобы равнодействующая внутренних сил (продольная сила ) равнялась этой внешней силе (рис.8):

Аналогично мысленно рассечём брус в пределах участка II и отбросим левую часть бруса. Чтобы уравновесить внешние силы F₁,F₂, равнодействующая внутренних сил (продольная сила ) должна равняться алгебраической сумме внешних сил F₁,F₂:

.

Аналогично, для остальных участков получим:

на участке III

на участке IV

;

на участке V

;

на участке VI

.

Продольные силы на IV,V и VI участках можно также определить, мысленно отбросив правую часть бруса и рассматривая равновесие его левой части. Для этого необходимо определить реакцию в заделке.

Согласно знакам продольных сил: брус на участках I,IV,V,VI будет растягиваться, а на участках II, III - сжиматься.

В соответствии с полученными результатами строим эпюру продольных сил (эпюра N, рис.8).

3. Определение поперечных размеров.

Требуемая площадь поперечного сечения i-ой ступени определяется по формуле

откуда диаметр сечения ступени бруса

.

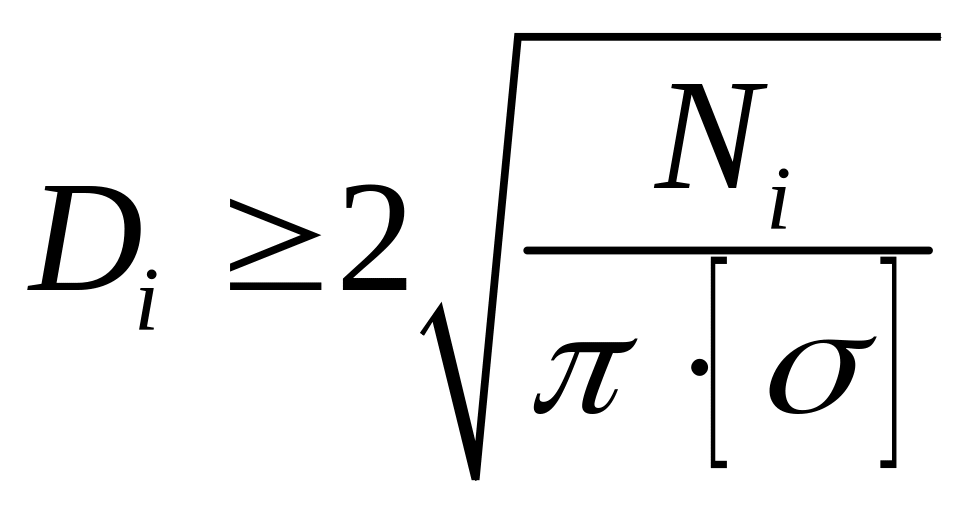Диаметр поперечного сечения бруса в пределах I и II участков (первой ступени) рассчитываем исходя из наибольшей по абсолютной величине продольной силы N

.

В соответствии с рядом нормальных линейных размеров (см. Приложение П.3^*) выбираем для этих участков размер .

Рис.8.

Площадь поперечного сечения ².

Аналогично, .

Согласно Приложения П.3 назначаем .

Площадь поперечного сечения .

Для последней ступени бруса

.

В соответствии с Приложением П.3 принимаем .

Площадь поперечного сечения .

4. Вычисление нормальных напряжений по участкам бруса

,

,

,

,

,

.

В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений (эпюра рис.8).

5. Определение удлинения бруса.

Полное абсолютное удлинение бруса равно алгебраической сумме абсолютных удлинений его участков:

,

,

или .

3.1.3. Пример расчета статически неопределимого бруса при нагреве

Н

Рис.9.

а рис.9 представлен составной ступенчатый брус, защемлённый с двух концов. Длины участков и их поперечные сечения взяты по рис.7, а именно: , , .

В отличие от примера 1 каждый из ступенчатых участков в данном примере выполнен из разных материалов: I участок – из стали, II – из алюминия, III – из бронзы.

Необходимые характеристики материалов ступеней представлены в таблице:

№ ступени	Материал	Модули упругости	Коэффициенты линейного расширения
I	сталь
II	алюминий
III	бронза

Требуется:

1. Определить степень статической неопределимости задачи.

2. Раскрыть статическую неопределимость, определив реакции опор.

3. Построить эпюры распределения продольной силы, нормальных напряжений и перемещений бруса.

Решение:

1. Определим степень статической неопределимости.

При изменении температуры защемлённого бруса его общая длина не меняется, а в защемлениях возникают реакции , сжимающие брус. Число реакции n_R =2.

Для расчетной схемы на рис.10 имеем одно уравнение статического равновесия вида: (n_у=1) или или , где X- продольная сила. Таким образом, для определения единственного внутреннего усилия, действующего в теле бруса, достаточно найти величину силы X. Однако решаемая задача является статически неопределимой, так как из рассматриваемого уравнения статического равновесия невозможно найти величину X.

Степень статической неопределимости n_H= n_R - n_у = 2-1=1, т.е система один раз статически неопределима.

Подобные задачи решаются путём добавления к уравнениям статики недостающего числа уравнений, получаемых из рассмотрения упругих деформаций тела. В данном случае число таких дополнительных уравнений равно единице.

Упругие деформации бруса компенсируют его удлинение , вызванное нагревом, которое имеет следующий вид:

,

где – температурное удлинение стального участка бруса,

– температурное удлинение алюминиевого участка бруса,

– температурное удлинение бронзового участка бруса.

Тогда

,

.

Деформация сжатия бруса, вызванная реакциями опор, выражается формулой

,

где – укорочение стального участка от силы X,

– укорочение алюминиевого участка от силы X, – укорочение бронзового участка от силы X.

Уравнение совместности деформаций, вызванное нагревом и реакциями заделок, имеет вид .

Данное уравнение позволяет найти продольную силу X=R_D=R_A=N

или

.

Расчёт нормальных напряжений

,

,

.

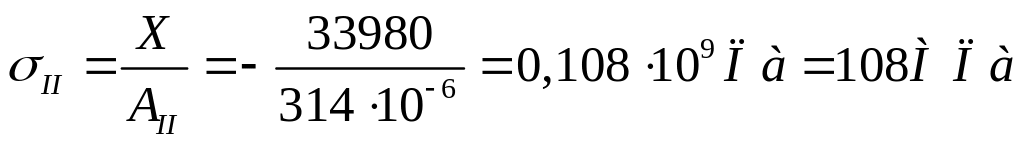Расчет перемещений от продольной силы

,

,

.

Результаты этих вычислений представлены на эпюрах рис.11.

Рис.11.