Функции, их свойства и графики.

1) Что называется функцией? Например.

2) Что такое область определения функции?

3) Что такое множество значений функции?

4) Какая функция называется возрастающей? Например.

5) Какая функция называется убывающей? Например.

6) Какая функция называется четной, нечетной? Например.

7) Какое свойство графиков четной, нечетной функции вам известны?

8) Исследовать на четность и нечетность функции y = x + ; y = x² + 3x⁴ − 2.

9) Какая функция называется линейной? Назвать ее свойства.

10) Какая функция называется прямой пропорциональностью? Назвать ее свойства.

11) Какая зависимость получается из линейной функции, если k = 0? Назвать ее

свойства.

12) Какая функция называется обратной пропорциональностью? Назвать ее

свойства.

13) Назвать свойства функции y = x

14) Назвать свойства функции y = x 15) Назвать свойства функции y =

16) Какая функция называется обратимой?

17) Дать определение взаимообратных функций.

18) Как расположены графики двух взаимообратных функции?

19) Каждая ли функция имеет себе обратную на своей области определения?

Например.

20) Сформулировать алгоритм нахождения функции обратной к данной.

21) Найти функцию, обратную к функции: a) y = 2x – 1

б) y = x , при x є (0 ; + ∞)

22) Сформулировать необходимое и достаточное условие существования обратной

функции.

23) С помощью каких геометрических преобразований можно построить график

функции y = f(x) + b, b > 0,если известен график функции y = f(x)?Например.

24) Дан график функции y = f(x). С помощью каких геометрических преобразований получить график функции y = f(x a)? Например.

25) Дан график функции y = f(x).Как построить график функции y = f(kx).

С помощью каких геометрических преобразований это можно сделать? Например.

26) Дан график функции y = f(x). Как построить график функции y =kf(x)?

Например.

Раздел I I. Степенная функция. П.2.1 Корень n-й степени и его свойства.

- обозначение корня n-й степени из числа а.

Знак называется корнем или радикалом.

n – показатель корня;

а – подкоренное выражение.

Извлечение корня – это операция обратная к операции возведения в степень.

Введем понятия корня n-й степени из числа а аналогично понятию квадратного корня из числа а.

Квадратный корень 1) Квадратным корнем из числа а называется такое число х, квадрат которого равен а, т.е. = х,если х² = а или = Например, , т.к. ;	Корень n-й степени 1) Корнем n-й степени ( n  2, n  N) из числа а называется такое число х, n-я степень которого равна а, т.е. , если или Например, , т.к. или , т.к. , т.к. и
Чтобы устранить двузначность корня n-й степени из числа а, вводят понятие арифметического корня.
2) Арифметическим квадратным корнем из числа а (а  0),называется неотрицательное число х, квадрат которого равен а, т.е. = х, если х2=а, х 0 ; а  0 Например, , т.к. ; 2  0.	2) Арифметическим корнем n-й степени ( n  2, n  N ) из числа а, где а  0 называется неотрицательное число х,n-я степень которого равна а, т.е. , если , а  0; х  0 Например, , т.к. , 2  0.

Рассмотрим решения уравнения х = a

	n - четное (n=2)	n – нечетное ( n=3)
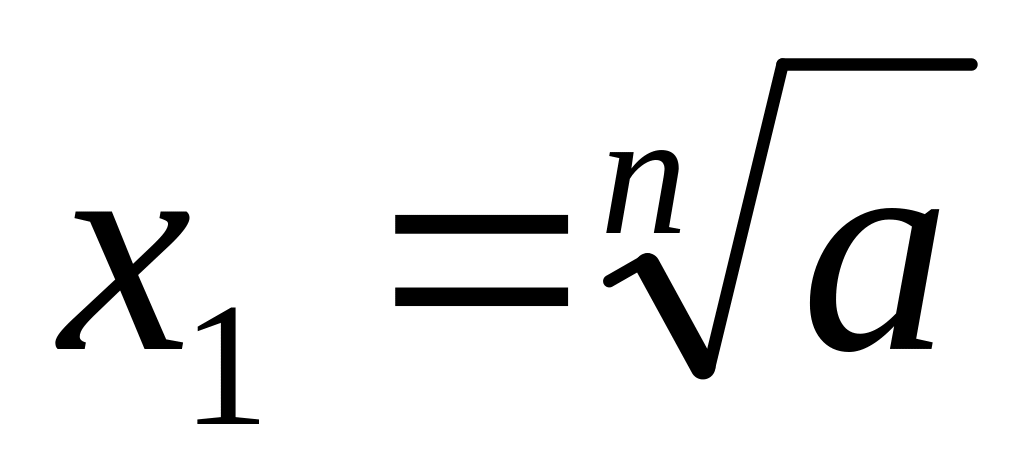а  0	;	;  0
а  0	корней нет	;  0
а = 0	х = 0	х = 0

Например: 1) , п = 2 – четное, а  0 ;
2) , п = 4 – четное, а = 81, а  0 , т.к. и
3) , п = 2 – четное, а = - 4, а  0 корней нет	-4
4) , п = 3 – нечетное, а = 27, а  0 , т.к.
5) , п = 3 – нечетное, а = - 27, а  0 х = -3, т.к.	0
6) , х = 2, т.к.

Для корней нечетной степени справедливо равенство:

Вывод: Для любого действительного а :

	 а  , если п - четно
	а , если п - нечетно.