П.5.4.Четность, нечётность тригонометрических функций.
Рассмотрим
точки
и
единичной окружности. Они имеют
координаты
соответственно и симметричные относительно
ОХ.
Таким
образом,
;
,
Px
что говорит о чётности
функции
и
нечётности функции
.
x
Для тангенса и котангенса при
допустимых значениях
имеем:
P-x
Значит, функции
и
- нечётные:
Например: 1) Определить знак выражения:
Вычислить:
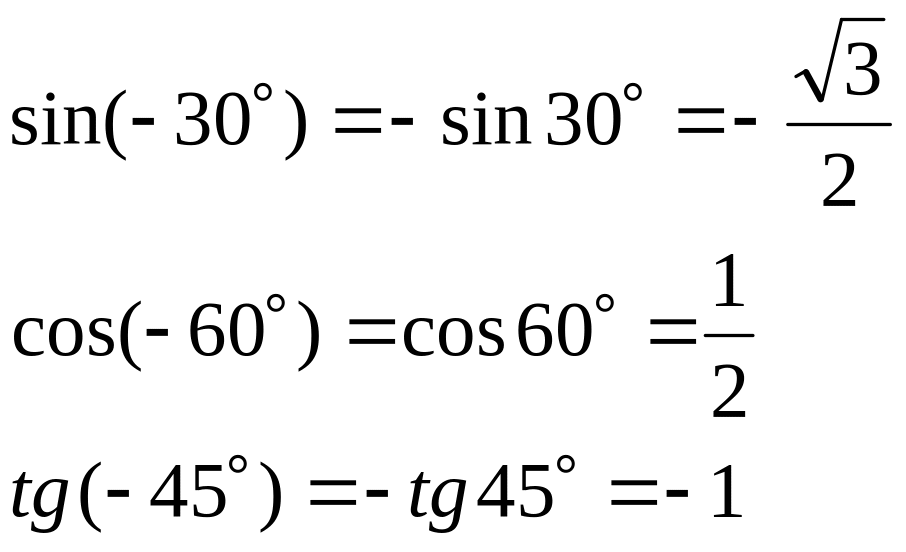
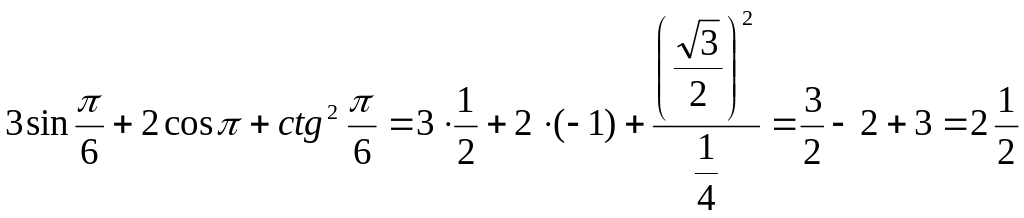
П.5.5. Периодичность тригонометрических функций.
Определение:
Функция
называется периодической с периодом
если для любого
из области определения функции, числа
и
также принадлежат области определения
и выполняется условие:
Нетрудно
доказать, что когда
- период функций
,
то все числа вида
,
где
так же являются периодами функции.
Действительно,
Применяя определения синуса, косинуса числового аргумента и учитывая их геометрическую интерпритацию на единичной окружности, имеем:
Для функций
и
Наименьшим
положительным периодом функций
(где
,
в-числа) будет
.
Опираясь на
периодичность тригонометрических
функций, можно находить значения функции
любого аргумента через значения функций
аргумента
для sin x и cos x и
для tg x и ctg x.
Например.
1) Вычислить наименьший положительный
период (Т')
функции
Решение. Для y = sin
x,
для
,
k =
,
.
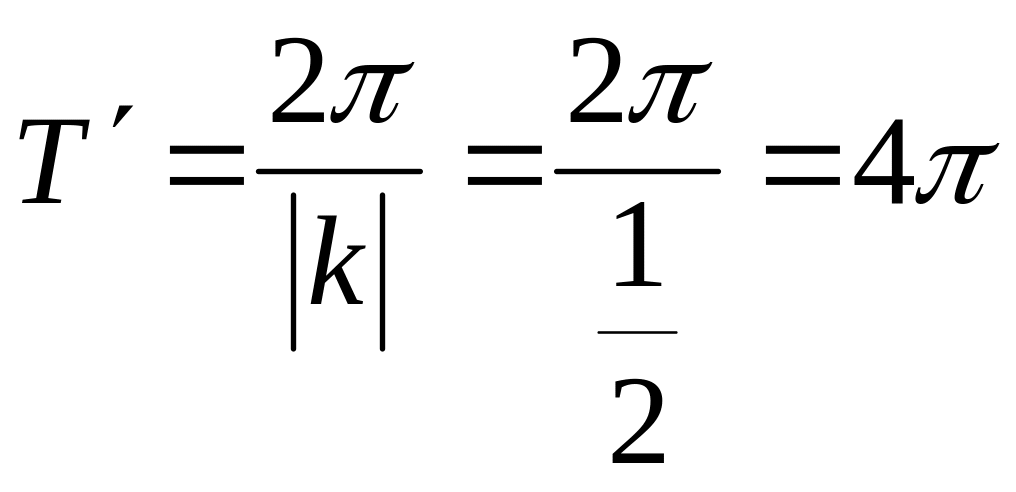Ответ: Т' = 4 .
2) Вычислить
наименьший положительный период (Т')
функции
Решение. Для y = cos x,
для
,
.
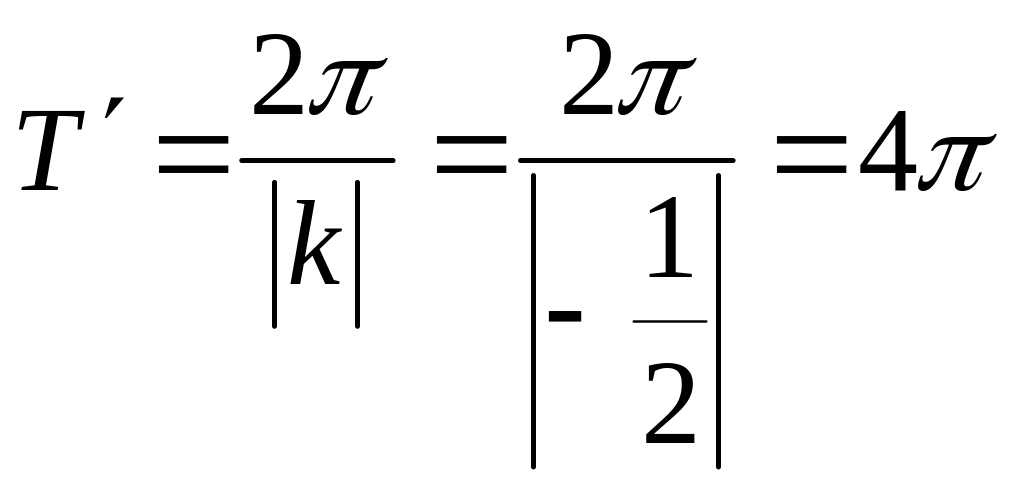Ответ: Т' = 4
2) Вычислить:
.
.
П.5.6. Основные свойства тригонометрических функций и их графики.
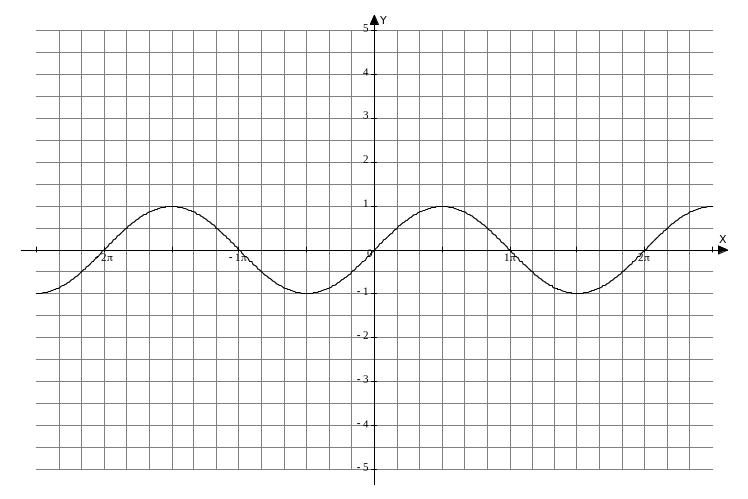
1. Функция y = sin x
График каждой из тригонометрических функций достаточно построить на промежутке, соответствующем наименьшему положительному периоду, а затем продолжить его построение на всей области определения.
Свойства функции:
1) D(y):
2)
3) Функция нечётная: для всех из области определения .
4) Функция периодична
с наименьшим периодом
.
5) Нулями синуса
есть точки
.
6) Функция возрастает
на интервалах: х є
,
.
и убывает на интервалах:
х є
.
7) Промежутками знакопостоянства функции есть интервалы:
для y > 0, x є
.
для y < 0, x є
.
График синуса называется синусоидой.
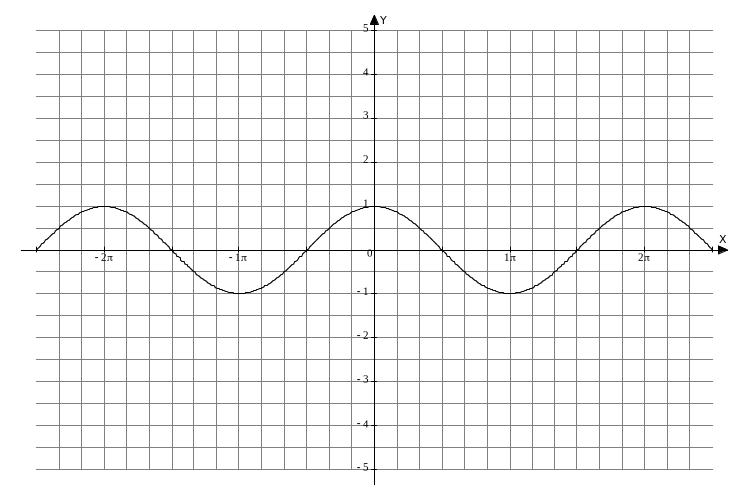
2. Функция y = cos x.
Свойства функции:
1)
2)
3) Косинус –
чётная функция:
для всех
4) Функция периодична с наименьшим периодом .
5) Нулями функции
являются точки
6) Функция
y = cos x
возрастает на интервалах: х є
,
,
и убывает на интервалах: х є
.
7) Промежутками знакопостоянства функции являются интервалы:
для y > 0, x є , ,
для y < 0, х є
(
),
.
График функции y = cos x называется косинусоидой
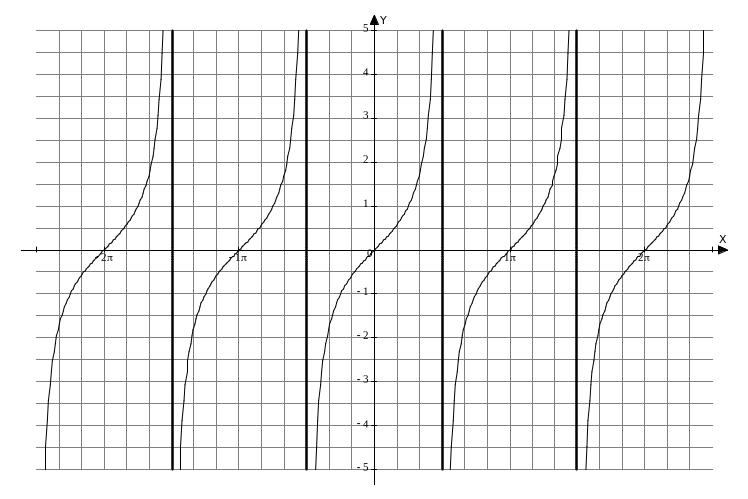
3. Функция y = tg x.
Свойства функции:
1)
.
2)
3) Тангенс –
нечётная функция :
.
4) Функция периодична с наименьшим положительным периодом .
5) Нулями
тангенса являются точки
,
.
6) Функция
возрастает на интервалах:
.
7) Промежутками знакопостоянства функции являются интервалы:
для
,
для
.
График функции называется тангенсоидой
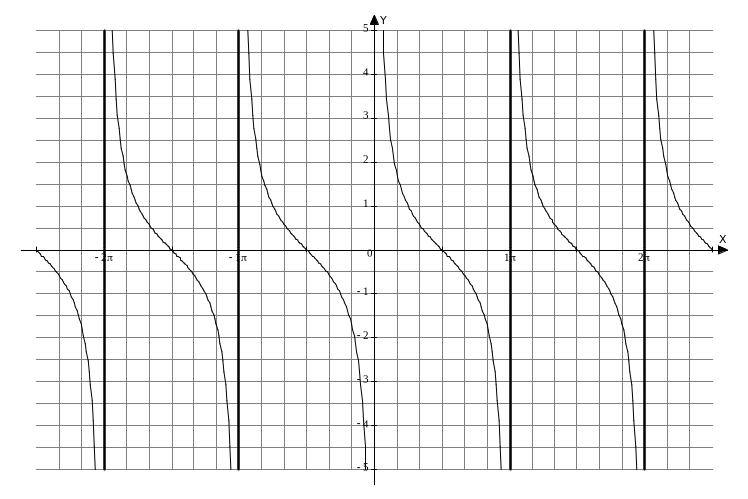
4. Функция y = ctg x.
Свойства функции:
1)
.
2)
3) Котангенс –
нечётная функция
4) Функция периодична с наименьшим периодом
5) Нулями функции
есть точки
6) Функция
убывает на интервалах
7)Промежутками знакопостоянства функции являются интервалы:
при
при
График функции называется котангенсоидой.
П.5.7. Гармонические колебания.
В математике
простым гармоничным или синусоидальным
колебанием называют функцию вида
Она описывает многие физические процессы.
Если, например, тело висит на пружине
и его вывести из положения равновесия,
то в идеальной ситуации (принебрегая
сопротивлением воздуха, нагреванием
пружины, и.т.д.), зависимость между
отклонением тела от положения равновесия
и временем х выражается формулой
.
Говорят, что данное
тело совершает гармонические колебания.
Исходя из физического смысла гармонического
колебания, константы
называют соответственно амплитудой,
частотой и начальной фазой колебания.
Функция
является
периодичной с наименьшим периодом
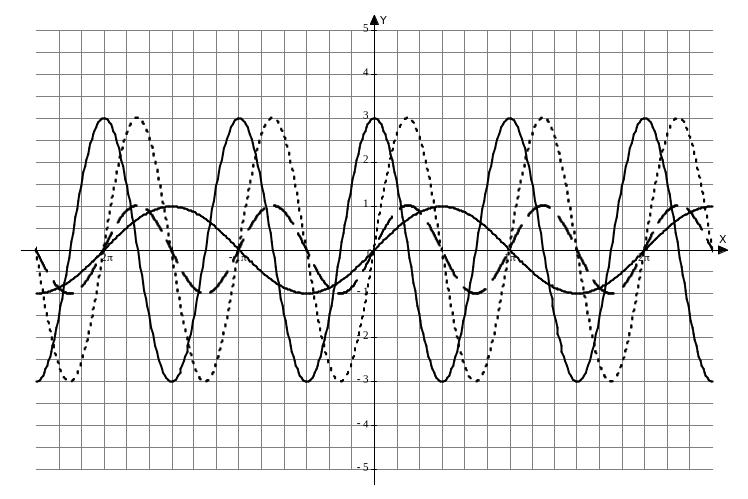
Например. Построить
график функции
.
Решение. Преобразуем
выражение данной функции в виде:
1) Строим график функции y = sin x.
2) Строим график функции y = sin 2x, сжимая график функции y = sin x, в 2 раза по
оси ОХ.
3) Строим график функции y = 3sin2x, растягивая график функции y = sin2x, по OY в 3 раза .
4) Строим график
функции
путем
параллельного переноса гра-
фика (3) вдоль оси OХ на влево(1,5 ед. отр.).
