П.1.5 Построение графиков функций с помощью геометрических преобразований известных графиков функций.

1. Построим график функции у = f (х)  b, b 0, если известен график функции у = f (х).

Искомый график можно получить из графика функции у = f (х) с помощью параллельного переноса его по оси ОУ на b единиц вверх или вниз.

Например. Построим в одной системе координат графики функций:

1) у = х ² ; 2) у = х² + 2 ; 3) у = х² - 2

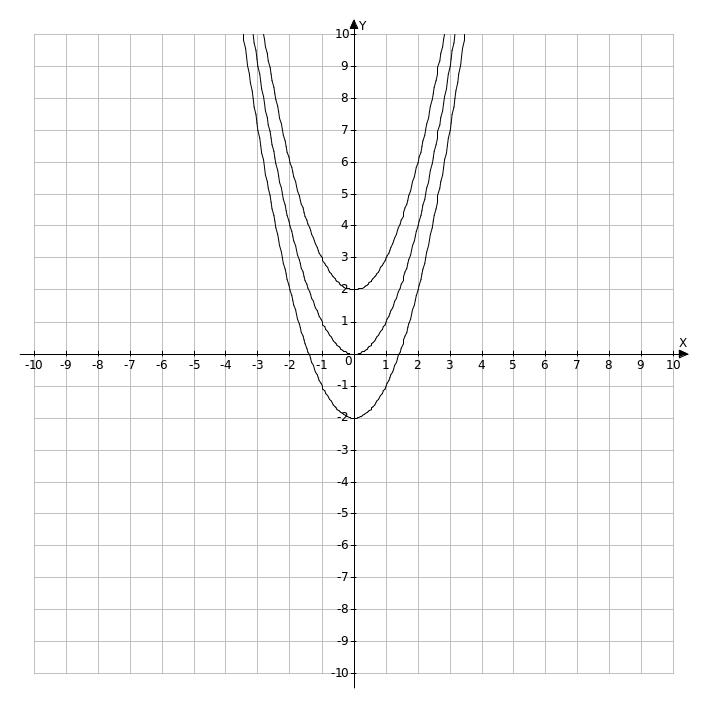
2. Известен график функции у=f(х). Надо построить график функции у=f(х+а)

График функции у = f (х + а) можно получить из графика функции у = f (х) путем параллельного переноса его вдоль оси ОХ на а единиц влево, а график функции у = f (х - а) - из графика функции у = f (х) путем параллельного переноса его на а единиц вправо.

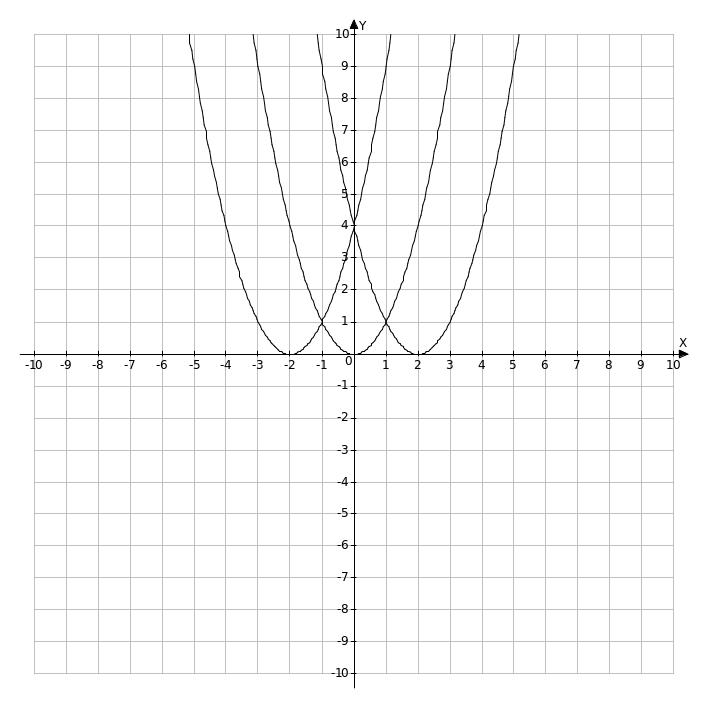
Например. Построим в одной системе координат графики функций:

у = х ² ; у = (х+2)² ; у = (х –2)²

3. Дан график функции у = f ( х ). Построить график функции у = k f (х)

График функции у = k f (х) получается из графика функции у = f (х) путем:

а) растяжения относительно ОУ в k раз, при k > 1

б) сжатия относительно ОУ в k раз, при 0 < k < 1

в) путем преобразования симметрии относительно ОХ графика функции

у = k f (х) ( k > 0 ), при k < 0 .

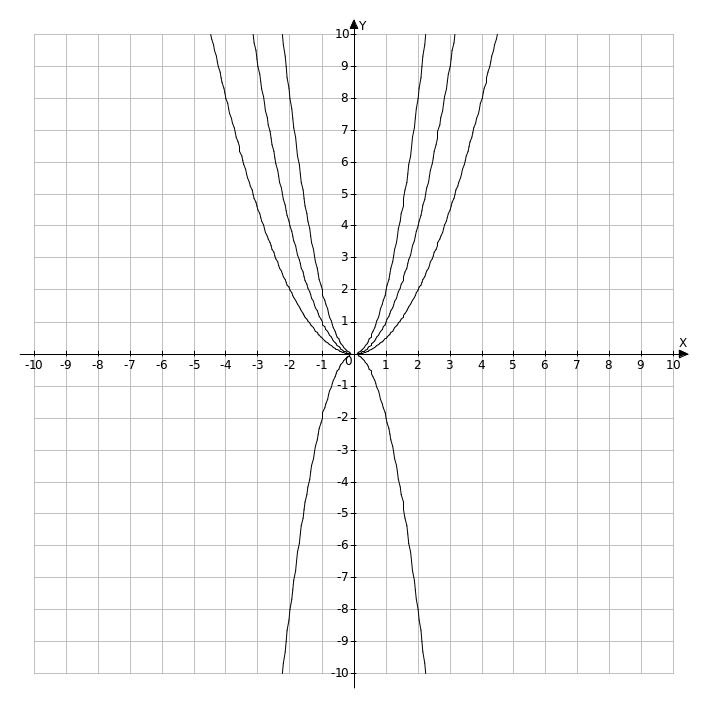
Например, 1)у = х ² ;

2)у = 2х² - растяжение графика функции у = х ² в 2 раза по ОУ;

3)у = х² - сжатие графика функции у = х ² в 2 раза по ОУ;

4)у = - 2х² - симметрия относительно графика функции у = 2х²

4. Дан график функции у = f ( х ). Построить график функции у = f ( kx ).

График функции у = f ( kх ) получается из графика функции у = f (х) путем:

а) сжатия по ОХ в k раз, если k > 1

б) растяжения по оси ОХ в k раз, если 0 < k < 1

в) путем преобразования симметрии относительно ОУ графика функции

у = f ( k х )( k > 0) при k < 0

Например, у = х ² ;

у = ( 2 х)² - сжатие графика функции у = х² в 2 раза по ОХ;

у = ( х)² - растяжение графика функции у = х ² в 2 раза по ОХ;

у = - ( х)² - симметрия относительно ОХ графика функции у = ( х)²

5 . Дан график функции у = f ( х ). Построить график функции у = f (|x|)

Как правило, в упражнениях, связанных с модулем, приходится освобождаться от модуля числа, пользуясь его определением.

По определению модуля числа, имеем:

f (|x|) =	f (х), если х  0;
	f (- х), если х  0

Для построения графика у = f (|x|) , достаточно построить график функции у = f (х) при х  0 , а затем его отобразить симметрично относительно ОУ.

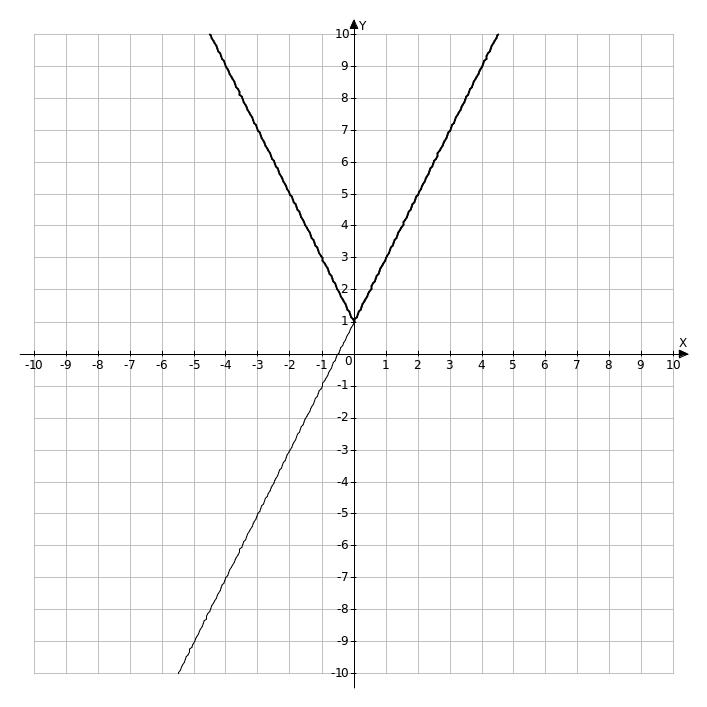
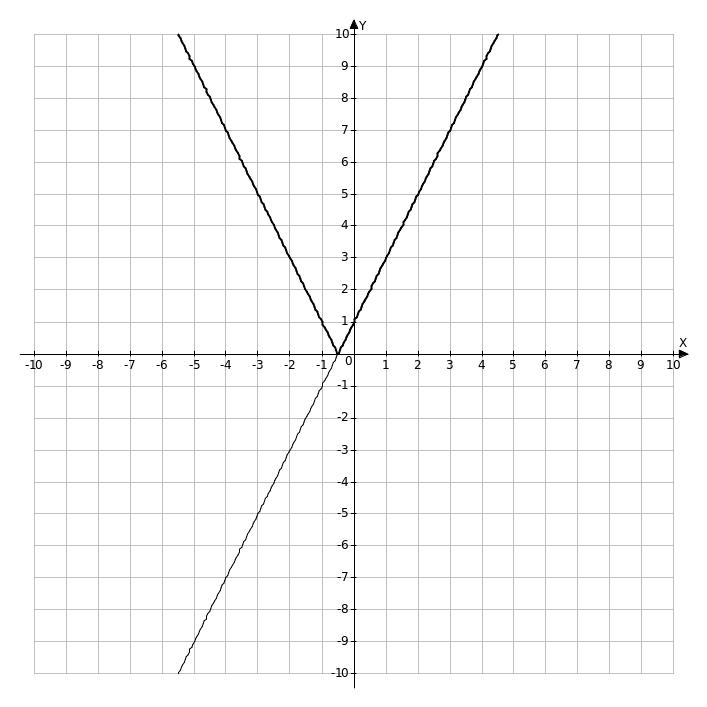
Например. Построить график функции у = 2 |x| + 1 .

Строим график функции у = 2х + 1, а затем ту часть графика, которая соответствует положительным значениям переменной х, отображаем симметрично относительно ОУ. y = 2x + 1

х	0	1	2
y	1	3	5

6. Дан график функции у = f ( х ). Построить график функции у = |f(x)|

Учтем, что:

|f(x)| =	f (х), если f (х)  0;
	- f(х), если f (х) 0

Значит, достаточно построить график функции у = f (x), а ту часть графика, которая лежит ниже ОХ, отобразить симметрично относительно ОХ

Н апример, у = | 2 x + 1 | .

Вопросы для повторения по теме