П.5.2. Радианная система измерения углов и дуг.

В тригонометрии рассматривают обобщенные понятия угла и дуги.

Угол – это величина, полученная при вращении луча вокруг начальной точки и характеризующая меру отклонения луча от своего начального положения.

ОА − начальное положение луча,

ОВ − конечное положение луча

AOB = , = + 360⁰ ∙ n, где n є Z,

n − число оборотов.

Д уга – это путь, пройденный точкой движения по окружности.

В зависимости от направления вращения луча различают положительные и отрицательные углы.

Углы, полученные при повороте луча против часовой стрелки ,считаются положительными, а по часовой стрелке – отрицательными. Углы и дуги измеряются в градусах и радианах.

Угол в 1⁰ – это угол, составляющий 1/360 часть полного оборота.

Угол в 1рад – это центральный угол, который опирается на дугу, длина которой равна радиусу окружности.

В ведение радианной системы обусловлено таким свойством дуг, которые соответствуют каждому центральному углу : для данного центрального угла отношение длин дуг концентрических окружностей к длине соответствующих радиусов является величиной постоянной.

Таким образом,

Установим соответствие между радианной и градусной мерами угла.

Центральному углу, равному 180⁰ , соответствует полуокружность, т.е. дуга длиной l= R.( ) (l_окр =2 R).

Чтобы найти радианную меру этого угла, надо длину дуги l разделить на R. Но из (*) : l/R= .Поэтому, 180⁰ = рад. Тогда, 1°= 0,01745рад; 1рад= 57,3

Пусть - градусная мера некоторого угла, а а- его радианная мера.

Так как градусная мера угла, образованного при одном обороте точки, равна 360 ,а его радианная мера равна 2 , то .Откуда

- формула перехода от градусной меры угла к радианной.

- формула перехода от радианной меры угла к градусной.

Например: 1) Определить радианную меру угла 108⁰.

2) Определить градусную меру угла, радианная мера которого 2,3 рад;

Для запоминания:

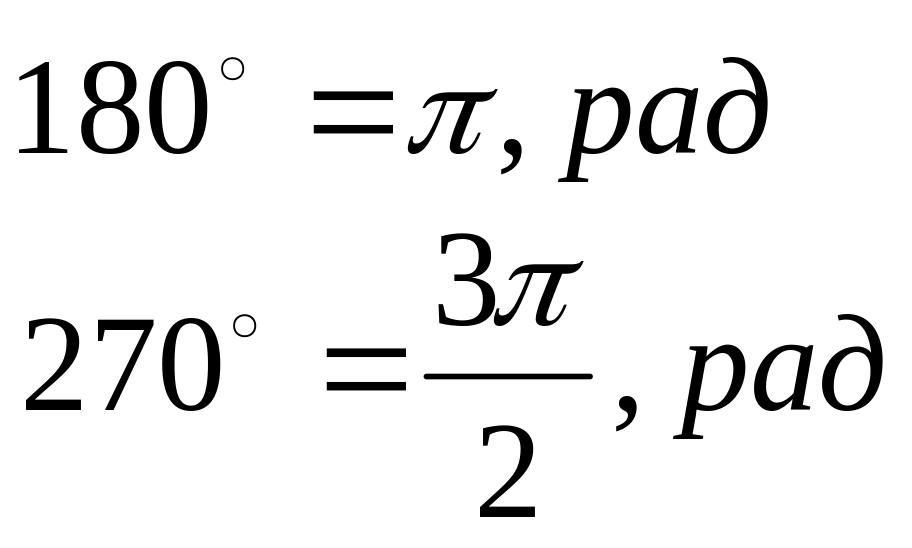
Радианная мера дает возможность ввести понятие тригонометрической функции произвольного аргумента.

П.5.3 Тригонометрические функции числового аргумента.

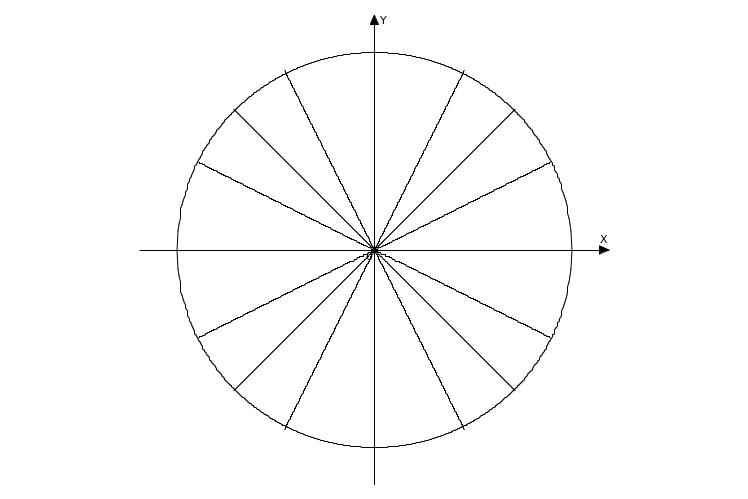
В тригонометрии рассматривают единичную окружность.

Определение. Единичная окружность-это окружность с центром в начале координат и радиусом равным единице.

Координатные оси делят единичный круг на четыре четверти. Начало отсчета ведется от точки Р₀ против часовой стрелки.

П усть - произвольное число, а Р – точка единичной окружности, полученная в результате поворота точки Р₀(1;0) на угол (рад) около точки О.

Каждой точке Р на единичной окружности соответствует определенная абсцисса

и ордината, которые зависят от числа .

Синусом числа называется ордината точки Р единичной окружности

(sin = y )

Косинусом числа называется абсцисса точки Р единичной окружности (cos =x )

Т ангенсом числа называется отношение , а котангенсом числа - отношение

Любому углу можно поставить в соответствие его sin или cos:

Поэтому , т.е. функции y=sinx и y=cosx заданы на множестве R.

Тангенс определен для всех x, кроме тех, у которых cos х=0.

Котангенс определен для всех x, кроме тех, у которых sin х=0.

Имеем:

Функции ; ; называют тригонометри-

ческими функциями числового аргумента.

Знаки тригонометрических функций.

sin cos tg ; ctg

Значения тригонометрических функций.

	0
	0				1				0								0
	1				0								0				1
tg	0		1		−				0		1		−				0
	−		1		0				−		1		0				−