Раздел IV.Логарифмическая функция. П.4.1. Логарифмическая функция, ее свойства и график.

Определение: Логарифмическая функция - это функция вида где

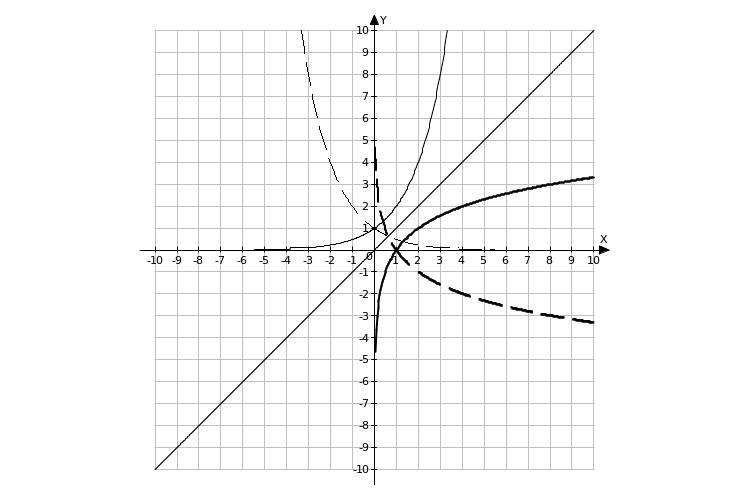
Это функция обратная к функции . Значит, график и показательной и логарифмической функций, имеющие одинаковые основания симметричны относительно прямой .

X	1	2	4
Y	0	-1	-2

X	1	2	4
Y	0	1	2

Свойства функции у=log_ax.

1)Область определения: х є .

2)Множество значений: у є .

3)Функция ни чётная, ни нечетная.

4)Нули функции: при

5) Промежутки монотонности :

если то функция убывает при

если то функция возрастает при

6) Промежутки знакопостоянства:

если то при при

если то при при

7)График функции проходит через точку

8)Асимптота:

П.4.2. Логарифмические уравнения.

Определение: Уравнения, в которых переменная величина находится под знаком логарифма или в его основании, называются логарифмическими:

log f₁(x) = log f₂(x),где f₁(x)>0;f₂(x)>0; (x)>0; (x)≠1.

Логарифмические уравнения являются трансциндентными, не имеют общего метода решения. Выделим основные приёмы решения таких уравнений.

I. Логарифмические уравнения, решаемые по определению логарифма:

log f(x)=b :

Например: а) решить логарифмическое уравнение log₃(x −2) = 4.

I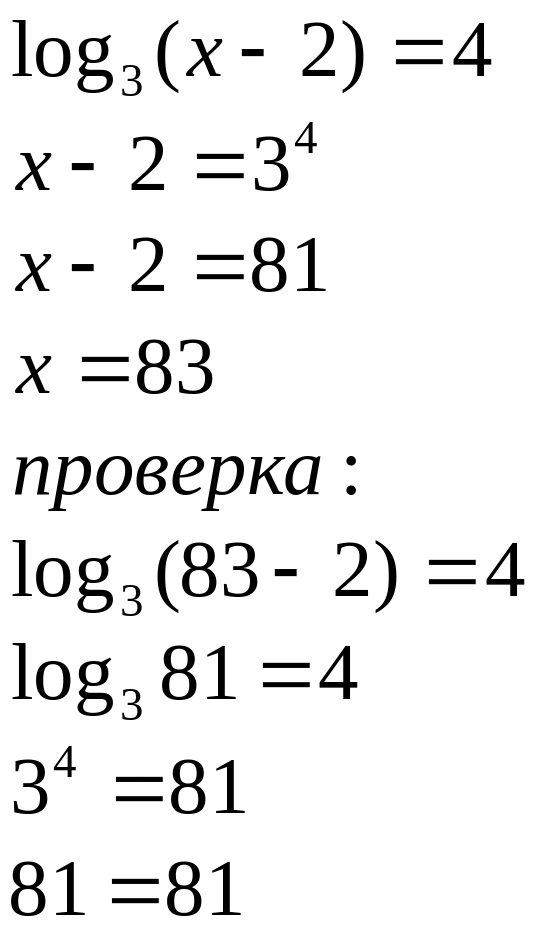 способ II способ

Ответ : 83

б) log ₂ (x²+4x+3)=3

x²+4x+3=2³

x²+4x+3=8

х²+4х−5=0

D=36; x₁=-5; x₂=1

Проверка:

1) log ₂ (25−20+3)=3 2) log(1+4+3)=3

log ₂ 8=3 log ₂ 8=3

2³=8 2³=8

8=8 8=8

Ответ: -5; 1.

в) log _x (x²-2x+2)=1, ОДЗ:

x¹=x²-2x+2

x²-3x+2=0

D=1; x₁=1; x₂=2

x₁=1 – не удовлетворяет ОДЗ

Ответ: x=1

Замечание: при решении логарифмических уравнений делают проверку или находят ОДЗ.