П.3.4.Простейшие показательные уравнения .

Определение. Показательными называются уравнения, у которых переменная стоит в показателе степени.

Рассмотрим простейшее показательное уравнение а^х=b, где и

Область значений функции - множество положительных чисел. Поэтому, в случае или уравнение a^x=b не имеет решений.

При уравнение a^x=b имеет единственный корень.

Если, вместо в показателе степени стоит некоторая функция , то уравнение имеет вид:

Общего метода решения показательных уравнений нет. Выделим несколько видов показательных уравнений и приведем способы их решений. Самым распространенным есть способ

I. Приведение обеих частей показательного уравнения к общему основанию.

а) чтобы решить уравнение , представляют в виде . Получают:

Например. Решить уравнения:

б)

Например.

в) решение уравнения с помощью основного логарифмического тождества:

Например. Решить уравнения:

II. Решение уравнения вида по определению логарифма .

Например: Решить уравнения:1) 2)

III. Приведениe показательных уравнений к квадратным.

Уравнение вида решается путем замены .

Тогда . Находим , и подставляя их в замену имеем: и .

Находим и .

Например. Решить уравнение:

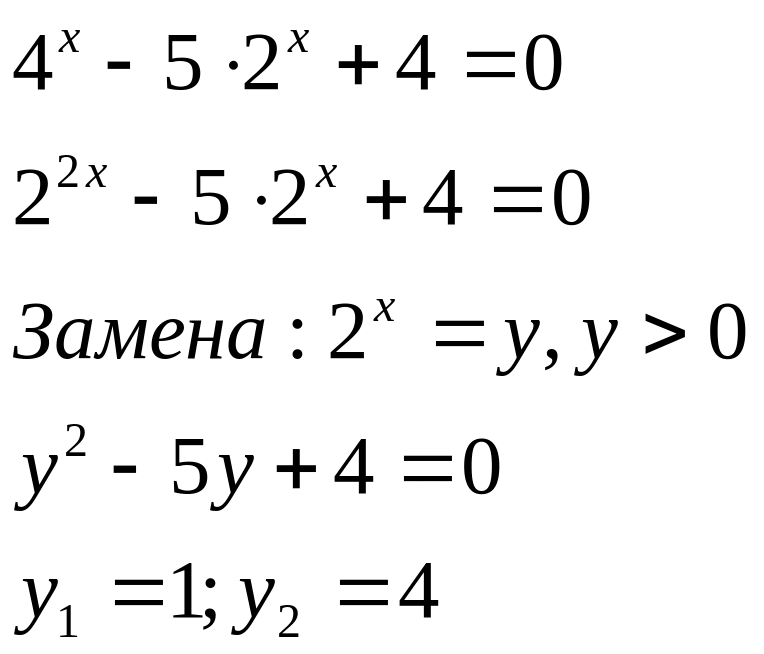
Учитывая замену, имеем: и

Ответ: 0 ; 2

IV. Способ вынесения общего множителя за скобку.

Например. Решить уравнение:

Ответ: 2

V. Способ приведения к общему показателю.

Например. Решить уравнение:

Ответ: 3

VI. Решение показательных уравнений путем логарифмирования обеих частей.

Например. Решить уравнения:

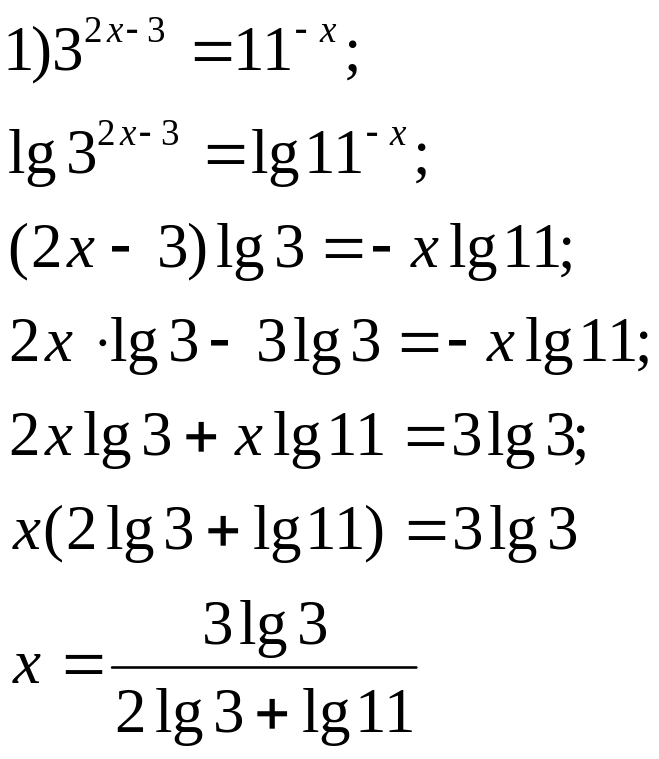
П.3.5. Показательные неравенства.

Показательные неравенства имеют вид:

или

Например. Решить неравенство: 1) 0,5 < 4

1 способ : 2 способ :

Решим неравенство методом интервалов:

+ — +

─── ────── ────

9

< y < 9

Учитывая замену, имеем:

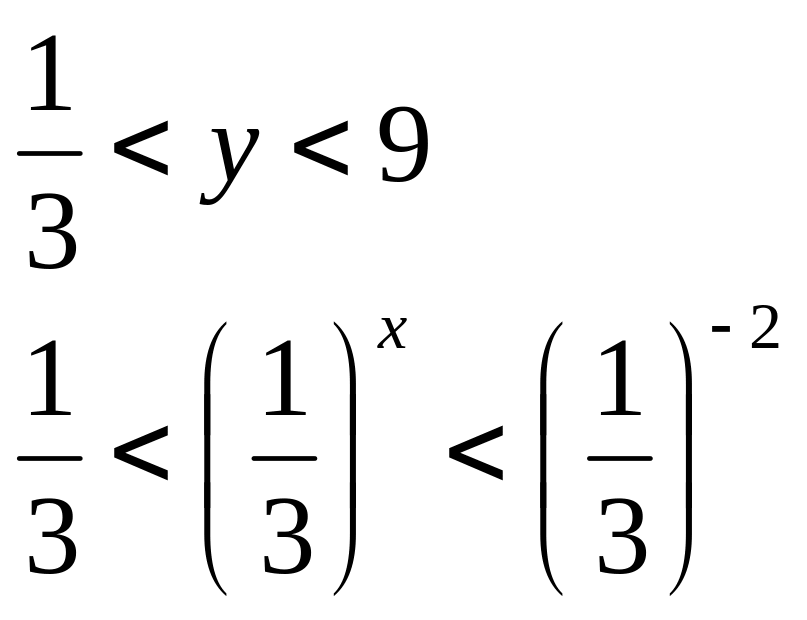
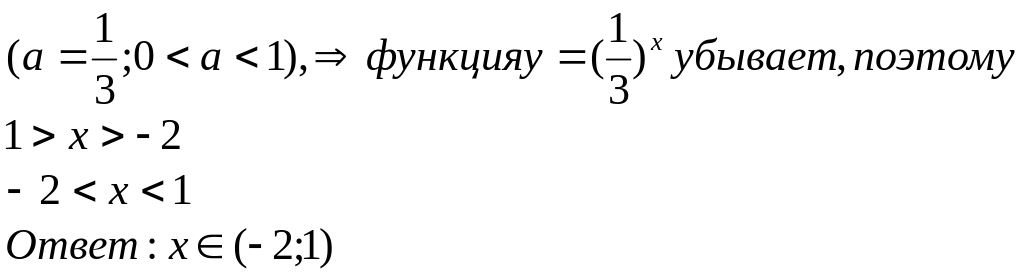
Вопросы для повторения по теме

Показательная функция.

1) Дать определение показательной функции y = a^x. Почему в нем вводится

ограничение а > 0 и а ≠ 1?

2) Назвать область определения и множество значений показательной функции.

3) Какие из функций y = x^1,3; y = 2,75^x; y = ; y = x⁻³; y = являются показательными?

4) Какие свойства имеет функция y = a^x , если а > 1? Построить эскиз графика этой функции? Привести пример такой функции.

5) Какие свойства имеет функция y = a^x , если 0 < а < 1? Объяснить, используя экскиз графика этой функции. Привести пример такой функции.

6) Сравнить и , если > и 0 < а < 1? Привести пример.

7) Сравнить и , если < , а > 1? Привести пример.

8) Сравнить и , если > ; < 0,5 .

9) Какие из функций: y = 0,26^x; y = ( )^x; y = ; y = 3^x; y = ; y = возрастают, а какие убывают?

10) Сравнить число а с единицей в каждом из неравенств:

а) а^1,27 > а^0,419; б) > ; в) > ; г) < .

11) Как расположены графики функций y = a^x и y = (а > 0; а ≠ 1) относительно

друг друга?

12) Какие процессы в области техники и естествознания описываются с помощью

показательной функции?

13) Какие уравнения называются показательными? Привести пример.

14) Сколько решений имеет показательное уравнение a^x = b, если b > 0; b = 0; b < 0?

Показать графически.

15) Что называется логарифмом числа по данному основанию?

16) По определению логарифма определить, какие из трех утверждений верны:

а) логарифм − степень;

б) логарифм − показатель степени;

в) логарифм − основание степени.

17) Найти: log₂(− 8) = ; 4 = ; log₃27=

18) Какие свойства логарифмов вы знаете?

19) Дать определение десятичного логарифма и натурального логарифма.

20) Записать основное логарифмическое тождество.

21) Записать формулу перехода к новому основанию.

22) Что значит прологарифмировать выражение? Например, прологарифмировать выражение х = 8ас².

23) В чем заключается способ решения показательных уравнений путем приведения

обеих его частей к общему основанию. Записать схему его решения. Например.

24)Как решаются уравнения вида а^f(x)=b по определению логарифма?

25) Решить уравнения:

а) 5^х = 5³; б) 17^х = 1; в) 4^х = ; г) (0,1)^х = 1000; д) = 81; е) 3^х = 5; ж) 3

26) Решить показательные уравнения способом вынесения общего множителя за скобки: а) 2^х+2 − 2^х = 96 б) 7^х − 7^х-1 = 6.

27)Как решаются показательные уравнения вида Аа^2х + Ва^х + С = 0? Записать схему их решения. Например, решить уравнения: а) 4^х + 2^х = 72 б) 7^2х − 6 ∙ 7^х + 5 = 0.

28) Решить уравнение способом приведения к общему показателю: 2^х · 5^х = 0,01

29) Решить показательные уравнения логарифмированием: а) 3^x = 8^x; б) 5^2x−1 = 7^−x.

30) Записать в аналитической форме показательное неравенство простейшего вида.

31) Какое свойство показательной функции y = a^x используется при решении показательных неравенств? Рассмотреть случаи а > 1 и 0 < а < 1.

32) Решить неравенства: а) 3^2-х > 27 б) 0,5^5-2х < 2 в) 2^5х+6 > ; г) > 6³.