1 курс / Л-2.2 (2) Постійний струм

Постійний електричний струм

7.1 Електричний струм. Сила струму. Густина струму.

7.2 Сторонні сили. Електрорушійна сила. Напруга.

7.3 Закон Ома. Опір кола.

7.4 Робота струму. Потужність. Закон Джоуля-Ленца

7.5 Закон Ома для неоднорідної ділянки кола.

7.6 Правила Кірхгофа.

7.1 Електричний струм. Сила струму. Густина струму.

В розділі «Електростатика» ми розглядали нерухомі заряди. В данному розділі розглянемо заряди, які рухаються.

Направлений рух заряджених частинок називають електричним струмом. Оскільки заряджені частинки можуть мати як додатній, так і від’ємний заряди то - за напрям струму прийнятий напрям руху позитивно заряджених частинок.

Величину заряду, що проходить через поперечний переріз провідника за одиницю часу називають силою струму

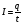. (7.1)

Вимірюється сила струму у системі СІ в Амперах (А). Це одна з основних одиниць в цій системі і визначається по взаємодії провідників із струмом.

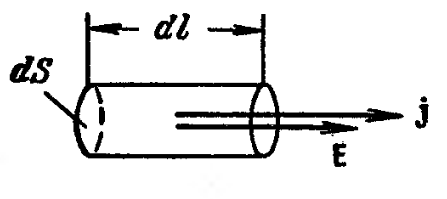
Для характеристики розподілу перенесення заряду по поперечному перерізу провідника введена густина струму j – це струм, який протікає через одиницю поперечного перерізу

. (7.2)

Не дивлячись на те, що струм величина скалярна, густина струму – це вектор, напрям якого співпадає з напрямом швидкості направленого руху позитивних зарядів, тобто

.

Силу струму, через густину струму знаходять шляхом інтегрування по площі перерізу провідника

. (7.3)

7.2 Сторонні сили. Електрорушійна сила. Напруга.

Умови існування електричного струму в провіднику:

1. Наявність вільних заряджених частинок (наприклад, в металевому провіднику – вільних електронів, в розчинах електролітів - іонів).

2. Наявність електричного поля в провіднику, яке діє на електричні заряди з силою F=qE (q –величина заряду, Е – напруженість електричного поля).

Електричне поле в провідниках створюється джерелами струму. В них відбувається переміщення зарядів проти сил електричного поля за допомогою різних видів енергії: механічної, оптичної, теплової, хімічної та інших, крім електростатичної. Ці сили, не електростатичного походження, називають сторонніми силами.

Джерело струму підтримує різницю потенціалів на кінцях провідника переносячи електричний заряд від одного кінця провідника з потенціалом φ₂ до іншого з потенціалом φ₁, проти сил електричного поля.

Роботу сторонніх сил, необхідну для перенесення одиничного позитивного заряду джерелом струму називають електрорушійною силою (е. р. с.).

. (7.4)

На рисунку нижче зображено графічне позначення однорідної ділянки електричного кола (а), неоднорідної ділянки (б) і повного кола (в). З рисунку видно, що однорідна ділянка кола 1 - 2 представляє собою провідник, в якому діють тільки потенціальні електричні сили. В неоднорідній ділянці кола діють і електростатичні сили і сторонні сили.

Роботу сторонніх сил вдовж всього кола можна знайти за формулою

.

Тоді повна робота сторонніх сил і сил електростатичного поля вдовж всього кола

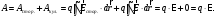, (7.5)

так, як робота електростатичного поля вдовж замкнутої траєкторії дорівнює нулю (циркуляція вектора напруженості електростатичного поля по замкнутій траєкторії дорівнює нулю).

Таким чином, повна робота по перенесенню заряду в колі виконується джерелом струму. Електричне поле виконує роботу лише на певних ділянках за рахунок джерела струму.

Робота по переміщенню заряду в неоднорідній дільниці кола (в якій є джерело струму, див. рис. б), виконується силами електричного поля і сторонніми силами на дільниці 1-2

Тут - робота, яку виконують сторонні сили по переміщенню одиничного позитивного заряду на ділянці кола 1-2. Величина

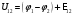(7.6)

називається спадом напруги або напругою. Напругою на ділянці кола 1-2 називають фізичну величину, що дорівнює сумарній роботі сил електростатичного поля і поля сторонніх сил по переміщенню одиничного позитивного заряду із точки 1 в точку 2.

Якщо на дільниці кола немає сторонніх сил, то напруга дорівнює різниці потенціалів між точками 1-2:

.

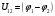При розімкненому колі, напруга на клеммах джерела струму дорівнює е.р.с. джерела:

.

Спад напруги, е.р.с. і різниця потенціалів в системі СІ вимірюються одиницюю – вольт (В).

7.3 Закон Ома. Опір кола.

Німецький фізик Г. Ом (1826 р.) експериментально встановив, що сила струму І в однорідному металевому провіднику (в якому немає сторонніх сил) пропорційна спаду напруги U на його кінцях:

, (7.7)

де R – електричний опір провідника.

Це рівняння виражає закон Ома для ділянки кола: Сила струму в провіднику прямо пропорційна прикладеній напрузі і обернено пропорційна опору провідника.

Одиницею опору провідника є:

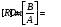(ом).

Опір металевого хімічно однорідного провідника довжиною l і поперечним перерізом s знаходиться по формулі

, (7.8)

де ρ – питомий опір провідника, який вимірюється в одиницях:

.

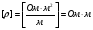Питомий опір провідника чисельно дорівнює опору провідника довжиною 1 м і площею перерізу 1 м². Питомий опір срібла 1,6∙10^-8 Ом∙м, міді- 1,7∙10^-8 Ом∙м, алюмінію 2,6∙10^-8 Ом∙м. Великий опір у сплава нікеля з хромом – ніхрому 110∙10^-8 Ом∙м.

Фізична величина обернена опору 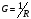називається електричною провідністю провідника і вимірюється в сіменсах .

Закон Ома можно представити в диференціальній формі:

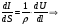
- закон Ома в диференціальній формі. (7.9)

Тут враховано, що густина струму, яка характеризує кожну точку провідника – вектор, 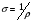- питома електропровідність провідника

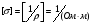
7.4 Робота струму. Потужність. Закон Джоуля-Ленца

Розглянемо однорідний провідник до кінців якого підведена напруга U. За час dt через поперечний переріз провідника проходить заряд dq = I∙dt. Роботу струму можна визначити так:

Якщо опір провідника R, то використовуючи закон Ома отримаємо:

Якщо провідник нерухомий, то вся робота струму іде на його нагрівання:

де dQ – елементарна кількість теплоти, виділена в провіднику. Тоді

_ Закон Джоуля- Ленца.

[Q] = [В∙А∙с] = Дж.

Тоді потужність:

.

Одиниця вимірювання в системі одиниць СІ: .

7.5 Закон Ома для неоднорідної ділянки кола.

Розглянемо неоднорідну ділянку кола з е.р.с. 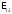і різницею потенціалів на кінцях . Якщо струм проходить по нерухомим провідникам, то робота всіх сил (і електричних і сторонніх) іде на нагрівання. При переносі заряду q, на дільниці 1-2 виконується робота

За час t в провіднику виділиться кількість теплоти

.

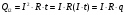Оскільки A₁₂ = Q₁₂ , то

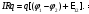
Після скорочення на q отримаємо вираз

- Закон Ома для неоднорідної ділянки кола

(узагальнений закон Ома)

З узагальненого закону Ома випливає, що:

1. Якщо дільниця кола 1-2 не має джерел струму, то 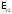= 0, і ми отримуємо закон Ома для однорідної дільниці кола

.

2. Якщо електричне коло замкнуте, то точки 1 і 2 співпадають, отже φ₁ = φ₂ , а значить φ₁ - φ₂ = 0, і ми маємо

.

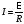В загальному випадку опір кола складається із зовнішнього і внутрішнього R +r. Тоді узагальнюючи отримаємо закон Ома для повного кола

.

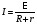3. Якщо коло розірвано, то струм І = 0. Це значить, що

.

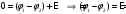Тобто, е.р.с. дорівнює різниці потенціалів на клеммах джерела струму.

7.6 Закони Кірхгофа для розгалужених електричних кіл

Дамо визначення декількох понять:

Вузол електричної схеми – це точка, в якій сходяться більше двох провідників.

Вітка – ділянка схеми між двома сусідніми вузлами.

Контур - довільна замкнута дільниця схеми.

Лінійно незалежні контури – це такі, які відрізняються по крайній мірі однією віткою.

Одним із методів розрахунку розгалужених електричних кіл є метод Г.Кірхгофа (нім. фізик), сформульованих ним у 1847 р.

Перше правило Кірхгофа: алгебраїчна сума струмів у вузлі дорівнює нулю

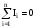(7.10)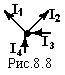

Струми, які направлені до вузла і від нього беруться з протилежними знаками.

I₄ + I₃ – I₂ - I₁ = 0

Друге правило Кірхгофа: Алгебраїчна сума спадів напруг вздовж будь-якого контуру дорівнює алгебраїчній сумі е.р.с., які увімкнені в цей же контур.

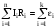(7.11)

В цих сумах знак (+) береться тоді, коли з довільно вибраним напрямком обходу контура співпадає довільно вибраний напрямок струму у вітці, чи напрямок дії е.р.с. В противному випадку береться (-). Для зображеної схеми рівняння 2-го правила Кірхгофа мають вид:

для контуру 1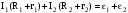

для контуру 2 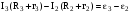.